Методическое пособие 659

3.4. Конечно-сходящийся алгоритм «Полоска-1»

Рассмотрим следующую систему условных рекуррентных неравенств в пространстве { }:

где t = 0, 1, 2, ...; at { };

(аt , ) – скалярное произведение векторов аt и ;t, t – вещественные числа.

Запись (< t ) в (3.19) означает, что вместо |...| t для

некоторых t (в частности, для всех t) может быть |. . .|< t. Относящиеся к этому случаю изменения также будут записаны в скобках (...).

Неравенство (3.19) для фиксированного t определяет полосу между двумя параллельными плоскостями в простран-

стве { }. Полосы по смыслу решаемой задачи могут быть заранее неизвестны: предполагается заданным некоторый алго-

ритм, доставляющий по значениям 0, ..., t вектор at { } и

числа t, t.

Будем предполагать выполненными следующие условия: а) существует такое > 0, что для любого t 0

б) существуют вектор * и число (0 < 1) такие, что при всех t 0 выполняется неравенство

Пусть выполняются условия а) и б). Введем обозначение:

Пусть κ – произвольное число, κ > min (1, 2 ). Для про-

извольного 0 следующий КСА решает условные неравен-

ства (3.14)

60

Заметим, что условие в скобках в (3.23) относится к случаю, когда в (3.19) знак «меньше».

Геометрическая интерпретация формул (3.23) проста (рис. 3.1). Если точка t находится в полосе (3.21), то τt 1 τt .

Если t лежит вне полосы (at ,τ) t κ t , то точка t+1 по-

лучается из t проектированием на «среднюю плоскость» полосы (3.19), т. е. на плоскость (at ,τ) t 0. Если же t

находится «близко» к полосе (3.19) (именно, еслиt < | t| <κ t), то точка t+1 получается проектированием t на ближайшую из плоскостей (at ,τ) t t .

Рис. 3.1. Геометрический смысл алгоритма «Полоска-1» [6]

61

Вектор t+1 всегда лежит в полосе (3.19). Таким образом, алгоритм (3.23) можно применять для решения безусловных рекуррентных неравенств, если только неравенство (3.19) относится к моменту времени t+1.

В частном случае можно взять κ = , тогда второй случай в (3.23) будет всегда отсутствовать и алгоритм (3.23) примет вид

Алгоритм предполагает знание числа , определяющего «запас» выполнения неравенств для некоторого = *.

Если < 1/2, то можно взять κ < 1; в этом случае алгоритм (3.23) приобретает особенно простой вид

Геометрическая интерпретация алгоритма (3.25) состоит в следующем: значение t+1 совпадает с t, если выполнено неравенство (3.19), и получается из t проектированием на плоскость (at ,τ) t 0 в противном случае.

Алгоритм, доставляющий значения at, t, t, может быть и таким, что эти значения зависят лишь от t, в этом случае неравенства (3.19) по существу заданы заранее; каждый из алгоритмов (3.23)–(3.25) доставит через конечное число шагов решение всех этих неравенств. В особенно простом случае неравенства (3.19) получаются циклическим повторением за-

данной конечной системы неравенств (т. е. at+T=at, t+T= t,

t+T= t для некоторого натурального Т). Таким образом, каждый из алгоритмов (3.23)–(3.25) может быть использован для решения конечной заданной системы неравенств (3.19).

Алгоритм «Полоска-1» позволяет рассчитывать программные задания на движение мобильного робота в зоне, свободной от препятствий, за короткий интервал времени.

62

3.5. Построение программных движений самоходной тележки

Рассмотрим задачу построения программных движений самоходной тележки, передвигающейся по цеху с препятстви-

ями (рис. 3.2).

Y,

м

10 di

8

Рис. 3.2. Тележка на участке с препятствиями

Положение тележки на плоскости 0XY определяется вектор-функцией

z(t) (x(t), y(t)),Ψ(t)), (3.26)

где x, у – координаты центра масс тележки;– курсовой угол тележки.

Программным движением zp(t) (t [t0, tT]) транспортной тележки будем называть такое ее допустимое движение, которое обеспечивает переход робота из произвольного начального состояния z(t0), z(t0) в желаемое конечное состояние z(tT), z(tT), при котором выполняется целевое условие.

63

Препятствия аппроксимируем на плоскости 0XY с помощью прямоугольников. Прямоугольные зоны, свободные от препятствий, характеризуются параметрами аi, bi, сi, di. Для обеспечения движения центра масс тележки без столкновения с препятствиями должны быть выполнены условия:

Окружим препятствия такой -окрестностью, чтобы достаточно было следить не за движением всей тележки, проекция которой на плоскость 0ХY имеет форму прямоугольника, а только за имитирующим ее вектором длины (с модулем l = |а – b|), проходящим через центр масс тележки с тем же

курсовым углом. Величину можно взять равной 1/2min(а, b), где а и b – длины сторон проекции тележки.

Функцию изменения курсового угла будем искать в виде полинома

j 1

где Р(t0) – начальное значение курсового угла; bj – искомые параметры движения.

При равномерном движении тележки вдоль оси 0X координата xР(t) центра масс определяется из выражения

где xР(t0) и xР(tT) – начальное и конечное значения координаты

xцентра масс тележки;

Т– период времени движения.

Программное движение центра масс тележки вдоль оси 0Y определяется интегральной зависимостью

где yР(t0) – начальное значение координаты y центра масс тележки.

64

Программное движение тележки, выбранное в классе функций (3.28)–(3.30), обеспечивает перемещение тележки в направлении, соответствующем курсовому углу Р(t). Параметры bj (j = 1, ..., N) полинома вида (3.28) выбирают так, чтобы удовлетворить условиям (3.27) обхода препятствий.

Текущим значениям t и (t) соответствуют xР(t, (t)) и yР(t, (t)), вычисляемые из (3.29), (3.30). При этом для i-ой свободной от препятствий прямоугольной зоны, определяемой из условия аi<xР (t, (t))<bi для координаты yР(t, (t)) согласно (3.27), должно выполняться неравенство ci < yР(t, (t)) < di. Для определения параметров bj, обеспечивающих выполнение этих неравенств, используется конечно-сходящийся алгоритм «Полоска-1», описанный в предыдущем пункте.

3.6. Построение программных движений манипулятора

Для проведения погрузочно-разгрузочных работ в цехе мобильному роботу достаточно иметь трехкоординатный манипулятор с цилиндрической системой координат.

Положение манипулятора мобильного робота в момент времени t однозначно определяется вектором обобщенных ко-

ординат q(t) = |qj(t)| или вектором декартовых координат

рабочего органа s(t) = |si(t)|ip 1 . Движение манипулятора однозначно определяется функциями q(t), q (t).

Программным движением манипулятора мобильного ро-

бота qР(t), t [t0, tT] будем называть такое его допустимое движение, которое обеспечивает переход схвата из произвольного начального состояния q(t0), q (t0) в желаемое конечное состоя-

ние q(tT), q(tT), при котором выполняется целевое условие.

С точки зрения построения траекторий, обеспечивающих огибание препятствий (станков), наиболее интересны вертикальное и горизонтальное движения манипулятора.

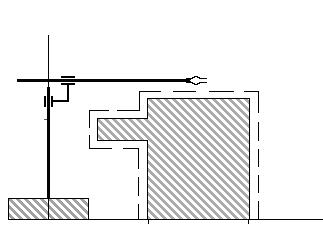
На рис. 3.3 изображены манипулятор, установленный на тележке, препятствие и система ортогональных координат 0xy.

65

В данном случае неравенства (3.33) должны быть выполнены для точки в центре схвата с координатами xP(t),

yP(t) при каждом t [t0, tT].

Примем для упрощения решения задачи движение yР(t) вдоль оси 0у равномерным

где yР(t0) и yР(tТ) – начальное и конечное состояния по координате 0у;

Т– время выхода в заданное положение по оси 0у. Движение хР(t) вдоль оси 0х будем искать в виде поли-

нома

i 0

где bi – искомые параметры программного движения.

Пусть параметры препятствий такие, что ci < yр(к) < di. Тогда для координаты 0х должны выполняться неравенства аi < xр(к) < bi при всех i, которые линейны относительно неизвестных коэффициентов полинома (3.35).

Система полученных линейных неравенств, порожденных препятствиями, разрешима, если только целевое условие вообще выполнимо в рассматриваемом классе движений (3.35). Применяя для решения полученной системы неравенств конечно-сходящийся алгоритм «Полоска-1» (явные формулы которого приведены в п. 3.4.), получим после конечного числа коррекций искомые значения параметров bi программного движения вида (3.35). Полученное программное движение, определяемое неравенствами (3.34), (3.35), достаточно плавное и удовлетворяет условиям (3.33).

Выполнение целевого условия манипулятором осуществляется в общем случае не единственным способом. Разные варианты траекторий возникают при изменении начальных параметров bi.

67

3.7.Сплайн-интерполяция задающих сигналов

Врезультате решения обратной задачи кинематики формируется массив значений обобщенных координат в ряде опорных точек на траектории движения манипулятора. Интерполяция траектории между опорными точками при планировании движений осуществляется с помощью сплайн-функций [7].

Рассмотрим задачу о приближении функции qj(t) на отрезке времени [0, T ]. Отрезок разбит на части

ющаяся многочленом степени на каждом из временных интервалов [ts–1, ts]:

S (qj, t) = Pj,s (t) = aj,s0 + , ... , + a j,s t , ts–1 < t < ts, (3.37)

удовлетворяющая условиям непрерывности самой функции и непрерывности ее производных до порядка – 1 в точках t1, t2, ... , tm –1:

(3.37), а соотношения (3.38) образуют систему из (m – 1) уравнений.

Остальные уравнения для коэффициентов получаются из условия близости к заданной функции и других условий. Простейшей задающей функцией может быть ступенчатый вход-

не удовлетворяющий условиям непрерывности (3.38). Возможность использования такого входного сигнала определяет-

68

ся свойствами электропривода и требованиями к качеству переходного движения.

Простейшей функцией, удовлетворяющей условию не-

прерывности, может быть линейный сплайн ( = 1). Общее число свободных параметров равно 2m.

Кроме m – 1 условий непрерывности потребуем совпа-

Исполнительный механизм робота с электроприводами представляет собой динамическую систему, которая способна отрабатывать достаточно плавные задающие сигналы. Вместе с тем рассчитанный кусочно-линейный входной сигнал при точном его выполнении порождает резкие импульсы ускорений и, следовательно, перегрузок. Поэтому для улучшения качества управления целесообразно использовать сплайны более высокого порядка. Интерполяция траектории кубическими полиномами, обеспечивающими непрерывность первых двух производных в узловых точках, называется кубическим сплайном. Преимуществом такой интерполяции является то, что относительно низкая степень полинома сокращает вычислительные затраты и в то же время задающие сигналы являются достаточно плавными.

Кубический сплайн записывается следующим образом:

Pj,s3(t) = aj,s0 + aj,s1t + aj,s2 t2 + aj,s3 t3, ts–1 < t < ts. (3.43)

69