
Методическое пособие 659
.pdf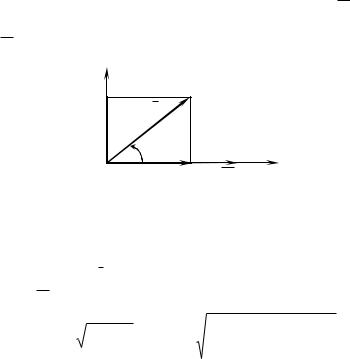
|
|
|
0 = ( 2max – L12i1x) R2 / L2, |
|
||
|
|
|
0 = –R2 L12 i1y / L2 + 0эл,ном sa 2max, |
(1.74) |
||
|
|
|
Мд = (рп L12 / L2) 2max i1y. |
|
||
|
|
|
Из системы (1.74) следует |
|
|
|
|
|
|
i1x = 2max / L12, |
i1y = L2 0эл,ном sa 2max / R2 L12. |
(1.75) |
|
|
|
|
Векторная диаграмма для проекций вектора тока статора |
|||
|
|
|
на оси x, y и вектора потокосцепления ротора 2 |
приве- |
||
i1 |
||||||
дена на рис. 1.6. Составляющая |
i1x является намагничиваю- |
|||||
щим током и при 2 = const i1x |
= const. Составляющая i1y |
|||||
представляет собой активный ток, которому при 2 = const пропорционален момент двигателя. Угол φ1 между векторами 2 и i1 является фазой тока.
y |
|
|
i1y |
|
|
i1 |
|
|
φ1 |
|
|
i1x |
2 |
x |
Рис. 1.6. Векторная диаграмма [1]
В соответствии с векторной диаграммой и уравнениями системы (1.75) получим соотношения для модуля I1max векто-
ра тока статора i1 и фазы тока φ1, позволяющие обеспечить условие 2 = const в динамических процессах:
I1max = |
i2 |
i2 |
2max |
1 |
L22 |
( |
|
s |
)2 |
, |
(1.76) |
|||||
|
||||||||||||||||
|
1x |
|
1y |
|
|
L12 |
|
|
2 |
0эл,ном a |
|
|
|
|||
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|||
|
φ1 = |
arctg |
i1y |
|
arctg |
L2 0эл,номsa |
. |
|
|
(1.77) |
||||||
|
i1x |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
||
При частотно-токовом управлении система управления преобразователем должна обеспечивать возможность форми-
30

рования первой гармоники тока статора для поддержания условия 2 = const в соответствии с уравнением
|
|
|
I |
ej( 0элt 1) . |
(1.78) |
i |
|
||||
1 |
1max |
|
|
||
Поэтому показанный на рис. 1.5 регулируемый источник тока (РИТ) снабжен, кроме входов управления амплитудой Uут и частотой Uуч тока, входом управления фазой тока Uуф.
Уравнение механической характеристики асинхронного двигателя в соответствии с уравнениями (1.74), (1.75) и с учетом малой некомпенсируемой постоянной времени Тэ имеет вид
Мд = ( 0– )/(Тэ Р+1), |
(1.79) |
где p2 22max /R2 ;
0 – угловая скорость вращения поля статора;
– угловая скорость вращения ротора.
Как показано на рис. 1.5, для измерения скорости на валу двигателя устанавливается тахогенератор G, с которого при постоянном магнитном потоке Фтг снимается пропорцио-
нальный скорости сигнал
Uпс = kпс , |
(1.80) |
при этом уравнение для канала регулирования частоты имеет вид
|
ω0эл = kf Uуч = kf kрм(Uзм + kпс ), |
(1.81) |
где kf – коэффициент пропорциональности по частоте; |
|
|
kpм |
– коэффициент усиления регулятора момента РМ. |
|
В |
соответствии с уравнениями (1.79)–(1.81) можно за- |
|
писать |
|
|
(Тэр + 1)Мд = (kf kpм /pп) (Uзм + kпс ) – = |
|
|
|
= ( kf kрм /pп) Uзм + ( kf kрмkпс /рп) – . |
(1.82) |
Подбором значений коэффициентов kрм и kпс обеспечивается критическая положительная связь по скорости
(kрмkпс)кр = рп /kf . |
(1.83) |
31

При этом уравнение механической характеристики запишется в виде
(Тэ р + 1)Мд = kмUзм, |
(1.84) |
где kм = kf kрм /рп. |
|
Разрешим (1.81) относительно Uзм |
|
Uзм = (1/kf kрм) 0эл – kпс . |
(1.85) |
С учетом (1.83) из (1.85) получим
Uзм = (1/kf kрм) 0эл – (рп /kf kрм) =
=(рп 0ном /kf kрм) 0эл /(рп 0ном) – (рп 0ном /kf kрм) / 0ном =
=(рп 0ном /kf kрм) ( 0 – ) / 0ном = 0эл,ном sa /kf kрм, (1.86)
где 0эл,ном = рп 0ном – электрическая угловая скорость поля при номинальной частоте f1ном токов статора;
sa = ( 0 – ) / 0ном – абсолютное скольжение. Соотношение (1.86) свидетельствует о том, что в схеме
(см. рис. 1.5) сигнал задания момента пропорционален абсолютному скольжению двигателя sa, поэтому рассматриваемый компенсационный способ иногда называют управлением по абсолютному скольжению.
В системе воспроизведения момента, приведенной на рис. 1.5, в канал регулирования тока введено нелинейное звено НЗ1, которое формирует сигнал задания амплитуды токов
статора Uyт.
Из уравнений (1.76) и (1.86) при Ψ2 = 2max = const
получаем
Uут = |
I1max |
2max |
1 |
L22 |
k2k2 U2 |
, |
(1.87) |
|
2 |
||||||
|
kут |
kутL12 |
|
f pм зм |
|
|
|
|
|
R2 |
|
|
|
где kут – коэффициент пропорциональности по току.
Для поддержания постоянным вектора потокосцепления Ψ2 в динамике у регулируемого источника тока предусмотрен вход управления фазой тока φ1. В канал регулирования фазы
32
тока введено нелинейное звено ΗЗ2, которое формирует сигнал задания Uyф.
В соответствии с уравнениями (1.77) и (1.86)
Uуф = |
|
|
1 |
arctg |
L2kf kр,мUз,м |
, |
(1.88) |
|
1 |
|
|
||||||
kуф |
kуф |
R2 |
||||||
|
|
|
|
|
где kуф – коэффициент пропорциональности по фазе. Динамические свойства электропривода с рассматрива-
емым способом регулирования момента определяются (1.84).
Контрольные вопросы
1.Каким образом формируются общие уравнения динамики манипулятора на основе аппарата Лагранжа?
2.Какие допущения принимаются при использовании уравнений Лагранжа второго рода?
3.Опишите расчетные схемы манипуляторов с декартовой, цилиндрической, сферической и угловой системами координат.
4.Выведите уравнения движения манипулятора с декартовой системой координат.
5.Получите уравнения движения манипулятора с цилиндрической системой координат.
6.Выведите уравнения движения манипулятора со сферической системой координат.
7.Получите уравнения движения манипуляторов с декартовой, цилиндрической, сферической и угловой системами координат в матричной форме.
8.Запишите дифференциальные уравнения, описывающие электропривод постоянного тока, и поясните физический смысл всех параметров.
9.Выведите уравнения для определения сигналов управления амплитудой и фазой тока статора асинхронного двигателя.
33
2.ПРЯМЫЕ И ОБРАТНЫЕ ЗАДАЧИ
ОПОЛОЖЕНИИ И СКОРОСТИ. УПРАВЛЕНИЕ ПО ВЕКТОРУ СКОРОСТИ
2.1. Задачи управления промышленными роботами
Рассмотрим возникающие на практике задачи управления манипулятором. Движение робота удобно задавать с использованием координат его рабочего органа в абсолютной системе координат пространства. В качестве такой системы примем прямоугольную систему координат c осями Ox1, Ox2, Ox3, показанными на рис. 1.1–1.4.
Задачу планирования движения рабочего органа в абсолютной системе координат пространства с учетом ограничений на перемещения, скорости и ускорения звеньев манипулятора и ограничений, связанных с препятствиями на пути его движения, должен выполнить стратегический уровень управления.
В соответствии с вектором X(t) координат рабочего органа система управления должна вычислить вектор q(t) обобщенных координат. Эта задача решается на тактическом уровне управления. Рассчитанный вектор q(t) передается на исполнительный уровень управления. Последний должен выдать управляющие сигналы на приводы сочленений, которые обеспечивают отработку вектора q(t) обобщенных координат.
При управлении движением манипулятора возникает ряд вопросов.
1.Должен ли робот отслеживать заданную траекторию или требуется лишь фиксировать рабочий орган манипулятора
внекоторых определенных положениях в пространстве?
2.Должен ли робот при движении вдоль заданной траектории отрабатывать определенный профиль скорости, т. е. должна ли скорость схвата изменяться в соответствии с заданной траекторией?
3.Если схват должен отслеживать заданную траекторию, а его скорость – изменяться в соответствии с заданным законом, то каковы допустимые отклонения действительного состояния робота от заданной номинальной траектории?
34
4. Являются ли все параметры манипулятора точно известными или некоторые из них переменны и неизвестны (например, масса переносимых грузов может изменяться в определенных пределах)?
Взависимости от ответов на эти вопросы решаются различные задачи управления движением манипулятора.
Большинство роботов, используемых в настоящее время
впромышленности, не предназначено для отработки заданной траектории в пространстве и не способно адаптироваться к изменению параметров.
Система управления такими роботами должна обеспечивать позиционирование рабочего органа в некоторых определенных точках декартового пространства. Положение рабочего органа в каждой опорной точке, заданное в декартовых координатах X(t), на тактическом уровне преобразуется в соответствующий вектор q(t) обобщенных координат, а на исполнительном уровне производится управление положением ро-
бота от точки к точке, т. е. позиционное управление.
Вряде сложных производственных задач необходимо обеспечивать желаемые скорости и ускорения рабочего органа робота при его движении вдоль заданной траектории (например, при покраске изделий или дуговой сварке). Поэтому более общей задачей робототехники является задача обеспечения практической устойчивости робота вблизи заданной тра-
ектории, т. е. контурного управления.
Всовременной робототехнике предъявляются более жесткие требования к эксплуатационным характеристикам роботов. В тех случаях, когда невозможно пренебречь неопределенностью и нестационарностью параметров манипулятора и свойств рабочей среды, применяют адаптивное
управление.
Вопросы планирования движения робота в рабочем пространстве с препятствиями, а также в пространстве обобщен-
ных координат, управления манипулятором с учетом его динамических свойств, адаптивного управления и реализации рассмотренных алгоритмов на основе микропроцессорной техники рассматриваются в следующих главах.
35
Настоящая глава посвящена решению задач преобразования вектора q(t) обобщенных координат в вектор X(t) координат рабочего органа и обратного преобразования, а также синтеза основанных на этих преобразованиях кинематических алгоритмов управления, которые не учитывают динамику манипулятора.
2.2. Кинематические уравнения общего вида
Соотношения, определяющие положения, скорости и ускорения исполнительного механизма без учета действующих на него сил и моментов, называют кинематическими уравнениями. Такие уравнения записывают для обобщенных координат qj и для координат xs, характеризующих положение контролируемой точки рабочего инструмента в базовой системе отсчета. В качестве базовой системы принята прямоугольная система 0х1х2х3.
В векторной форме кинематические уравнения имеют вид
Х(t) = F[q(t)], |
(2.1) |
где Х(t)={х1(t), х2(t), х3(t)}т – вектор-столбец декартовых координат рабочего органа;
q(t)={q1(t), q2(t),…, qп(t)}т – вектор-столбец обобщенных координат манипулятора.
Кинематические уравнения решают прямую задачу кинематики. Ее содержание заключается в определении положения рабочего органа (или звена механизма) в базовой системе отсчета по обобщенным координатам.
В скалярной форме кинематические уравнения имеют вид
хs(t) = fs[q(t)], s = 1, 2, 3. |
(2.2) |
При синтезе алгоритмов управления и исследовании динамики управляемых механизмов возникает необходимость рассматривать уравнения кинематики для скоростей. Такие уравнения получаются дифференцированием (2.1) по времени
X (t) = J[q(t)] q (t), |
(2.3) |
|
|
|
36
где матрица частных производных
J(q)= |
F(q) |
|
f |
|
(q) |
= [fsj(q)], |
s=1, 2, 3, |
j =1, 2, ..., n (2.4) |
||
|
= |
|
s |
|
|
|||||
q |
qj |
|||||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
называется матрицей Якоби, а ее определитель – Якобианом.
Матрица Якоби имеет размерность (3 n).
В раскрытой форме уравнения (2.3) имеют вид
n |
fs(q) |
qj (t), |
s = 1, 2, 3. |
(2.5) |
xs (t) |
|
|||
|
qj |
|
|
|
j 1 |
|
|
|
При синтезе алгоритмов управления необходимо также решать обратную задачу кинематики. Е содержание заклю-
чается в определении обобщ нных координат qj, j = 1, 2, ..., n, по заданным координатам положения и ориентации рабочего органа в базовой системе отсч та. Обратная задача кинематики разрешима не для каждой кинематической схемы манипулятора. Условия разрешимости зависят от числа степеней подвижности, типа кинематических пар и других факторов.
В том случае, если матрица Якоби квадратная, решение обратных задач кинематики записывают так:
q(t)=F |
–1 |
[Х(t)]; |
q (t)=J |
–1 |
|
(2.6) |
|
|
[q(t)] X (t), |
||||
|
|
|
|
|
|
|
где F –1, J–1 – вектор-функции, обратные к F и J соответственно.
Втом случае, если матрица Якоби не квадратная, вместо обращения матрицы используют квазиобращение.
Далее мы будем рассматривать такие кинематические схемы исполнительных механизмов, для которых указанные в (2.6) операции разрешимы аналитически или алгоритмически.
Вобщем случае кинематические уравнения исполнительных механизмов составляют для переносных и ориентирующих (рабочий инструмент) степеней подвижности. Мы
будем далее изучать в основном задачи управления переносным движением, поэтому при составлении уравнений ориентирующие степени подвижности не учитываются. Синтез алгоритмов управления ориентирующими движениями можно выполнить по локальным моделям.
37
Кинематические уравнения механических систем выводят обычно, рассматривая движение каждого звена и его связи с другими звеньями цепи. Если кинематическая цепь имеет сложную конфигурацию и много степеней подвижности (4–5 и более), то кинематические уравнения получают с помощью специального аппарата, использующего матричные преобразования и так называемые однородные координаты [2]. Такие уравнения удобны для анализа с помощью ПК.
Втех случаях, когда кинематические схемы механизмов просты, а число степеней подвижности не превышает тр х, уравнения кинематики целесообразно выводить непосредственно по расч тным кинематическим схемам. Такой подход мы будем использовать при выводе кинематических уравнений для манипуляторов, работающих в цилиндрической, сферической и угловой системах координат. Для манипулятора с декартовой системой координат преобразования переменных не требуются, так как он работает непосредственно в базовой системе отсч та.
Впоследующих разделах мы получим уравнения кинематики и рассмотрим прямые и обратные задачи для тр х типов кинематических схем тр хкоординатных манипуляторов.
2.3. Прямая и обратная задачи кинематики при управлении манипулятором
в цилиндрической системе координат
Возвратимся к расчетной схеме, представленной на рис. 1.2.
Связь между декартовыми координатами x1, x2, x3 груза массой m и обобщенными координатами , l, r имеет вид
x1 r sin , |
x2 r cos , |
x3 l. |
(2.7) |
Дифференцируя (2.7) по времени, получим уравнения кинематики для скоростей:
x1 r sin r cos , |
x2 r cos r sin , |
x3 |
l |
. (2.8) |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
38

Кинематические уравнения (2.7), (2.8) можно записать в векторной форме. Для принятых обозначений обобщенных
координат q1 = , q2 = l, q3 = r уравнения (2.7) примут вид
x1 = |
q3sin q1, |
x2 = q3cos q1, |
x3 = q |
2. |
(2.9) |
Введем следующие обозначения: |
|
|
|
||
f1(q) |
= q3sin q1, |
f2(q) = q3cos q1, |
f3(q) = |
q2, |
(2.10) |
тогда выражения (2.9) приобретут форму уравнений (2.1). Уравнения кинематики для скоростей записываем со-
гласно (2.2).
Матрица Якоби определяется из выражения
|
F(q) |
|
|
|
q3sinq1 |
|
q3cosq1 |
|
0 |
sinq1 |
|
|
||||||||||
J(q) = |
= |
|
q |
|
cosq |
|
|
= q sinq |
|
0 |
cosq |
|
|
. (2.11) |
||||||||
q |
|
|
q |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
3 |
|
1 |
|
3 |
|
1 |
|
|
|
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
q2 |
|
|
|
0 |
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вектор скорости определяется уравнением |
|
|
|
|
||||||||||||||||||
|
|
|
x |
|
|
q cosq |
|
0 |
sinq |
|
|
q |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
= |
|
|
|
|
|
|
1 |
|
|
(2.12) |
|||||||
|
X = |
x2 |
|
q3sinq1 0 |
cosq1 |
|
q2 |
. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
0 |
|
|
|
|
|
|
|
|
|||
|
|
|
x3 |
|
|
|
|
|
|
q3 |
|
|
|
|
||||||||
Решение обратной задачи кинематики для рассматриваемого манипулятора получается из системы уравнений (2.7):
|
|
x1 |
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
, |
l = x3, |
r |
x1 |
x3 . |
(2.13) |
||||||
arctg |
|
|
|
||||||||||
|
x2 |
|
|
|
|
|
|
|
|
|
|
||
Скорости изменения обобщенных координат находим |
|||||||||||||
дифференцированием по времени уравнений (2.13): |
|
||||||||||||
|
х1 x2 x |
1 х2 |
|
|
|
|
|
х1 x1 х2 x2 |
|
||||
|
|
|
|
|
, |
l |
х3 , |
r |
|
|
. |
(2.14) |
|
|
x21 x22 |
|
|
x12 x22 |
|||||||||
Отметим, что в (2.13) необходимо принимать главные значения arctg(x1/x2), которые ограничены пределами от – /2
39
