Методическое пособие 659

6.4. Программная реализация алгоритмов решения прямой и обратной задач кинематики

Прямая задача кинематики для любой кинематической схемы манипулятора решается однозначно. Ранее получены выражения (2.7), (2.16) и (2.23), позволяющие аналитически определить положение рабочего органа трехкоординатных манипуляторов, работающих в цилиндрической, сферической и угловой системах координат.

Решение обратной задачи кинематики для рассмотренных манипуляторов в соответствии с уравнениями (2.13), (2.15), (2.20), (2.22), (2.26), (2.32) и (2.33) также не вызывает затруднений. Однако не для всех манипуляторов можно получить аналогичные уравнения.

Рассмотрим расчетную схему манипулятора, содержащего поворотную платформу, вертикальную и горизонтальную степени подвижности, а также устройства для ориентации схвата. Управление движением осуществляется по трем угловым координатам. На рис. 6.7 схематично показаны вертикальная степень подвижности с длиною l1, горизонтальная степень подвижности с длиною l2, а также система обобщен-

ных координат 1, 2, 3 манипулятора и система декартовых координат x1, x2, x3 рабочего пространства.

трехкоординатного манипулятора

160

Прямая задача кинематики для рассматриваемой расчетной схемы решается следующим образом:

Уравнения кинематики для скоростей, соответствующие (6.4), имеют вид

x3 = (l2 sin 3 3– l1 sin 2 2) cos 1 –

– (l1cos 2 – l2 cos 3) sin 1 1.

Рассмотрим решение обратной задачи кинематики для трехкоординатного манипулятора, представленного на рис. 6.7, методом последовательных приближений (или метод итераций) [24].

Из уравнений системы (6.5) следуют выражения для определения первых производных от обобщенных координат в зависимости от скоростей схвата рассматриваемого манипулятора по координатам декартового пространства:

l2 sin ( 3 – 2)

161

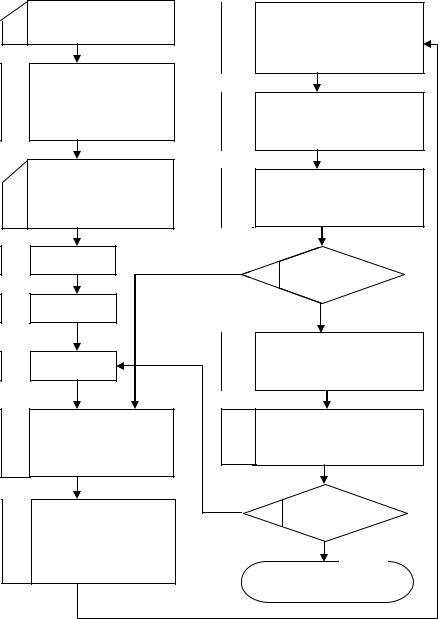
Для решения обратной позиционной задачи в среде DELPHI 5.0 разработана программа 1, алгоритм которой представлен на рис. 6.8. Он выполнен по итерационной схеме [25].

На начальном этапе вводятся длины звеньев l1, l2 манипулятора, число m опорных точек, допустимая среднеквадратичная погрешность Е, определяются типы массивов, переменных и процедура STRAIGHT решения прямой задачи кинематики. Далее вводятся исходные угловые координаты 1,2, 3 манипулятора и массивы X1C, X2C, X3C координат опорных точек на траектории движения схвата.

В ходе отработки цикла итерации для текущих значений угловых координат манипулятора решается прямая задача кинематики, определяется среднеквадратичное отклонение схвата от целевого состояния, вычисляются требуемые приращения и формируются новые значения угловых координат.

Циклы итераций повторяются до тех пор, пока среднеквадратичное отклонение схвата не уменьшится до величины заданной погрешности Е и соответствующие значения угловых координат не будут удовлетворять ограничениям на обобщенные координаты. После этого полученные в последнем цикле значения угловых координат выводятся как результат решения обратной задачи кинематики.

Необходимо отметить, что даже для трехкоординатного манипулятора обратная задача кинематики решается неоднозначно. Проверка соответствия результатов решения естественным кинематическим ограничениям на обобщенные координаты позволяет получить единственный приемлемый вариант.

Помимо итерационного метода, обратная задача кинематики может быть решена методом обратных преобразований или с помощью тригонометрического подхода [3]. Выбор метода для решения конкретной задачи определяется спецификой кинематической схемы манипулятора, а также опытом исследователя.

162

Программа 1

implementation const PI=3.14159;

L1=500; L2=765; { длины звеньев манипулятора }

B1,B2,B3: real; {массив рассчитанных угловых координат} X1C,X2C,X3C: arr; {массив заданных декартовых координат} {$R *.DFM}

{Ввод исходных угловых и заданных декартовых координат} procedure TfmExample.Button1Click(Sender: TObject);

begin B1:=StrToFloat(Edit1.Text); B2:=StrToFloat(Edit2.Text); B3:=StrToFloat(Edit3.Text); X1C[1]:=StrToFloat(Edit4.Text); X2C[1]:=StrToFloat(Edit5.Text); X3C[1]:=StrToFloat(Edit6.Text); X1C[2]:=StrToFloat(Edit7.Text); X2C[2]:=StrToFloat(Edit8.Text); X3C[2]:=StrToFloat(Edit9.Text);

X1C[3]:=StrToFloat(Edit10.Text);

X2C[3]:=StrToFloat(Edit11.Text);

X3C[3]:=StrToFloat(Edit12.Text);

end;

{Процедура решения прямой задачи кинематики} procedure STRAIGHT(B1,B2,B3:real;var X1,X2,X3:real); begin

164

S1:=sin(B1); { вычисление тригонометрических функций } S2:=sin(B2);

S3:=sin(B3);

C1:=cos(B1);

C2:=cos(B2);

C3:=cos(B3);

S23:=sin(B3-B2);

X1:=(L1*C2-L2*C3)*S1; { текущие декартовые координаты}

X2:=L1*S2-L2*S3; X3:=(L1*C2-L2*C3)*C1;

end; { конец процедуры STRAIGHT } {Процедура решения обратной задачи кинематики} procedure TfmExample.Button3Click(Sender: TObject); LABEL 1,2,3,4;

var j: integer; begin

FOR j:=1 TO 3 DO begin

1: repeat STRAIGHT(B1I,B2I,B3I,X1T,X2T,X3T);

{ отклонения схвата от целевого положения } DX1:=X1C[J]-X1T;

DX2:=X2C[J]-X2T;

DX3:=X3C[J]-X3T;

{среднеквадратичное отклонение схвата } U:=SQRT(DX1*DX1+DX2*DX2+DX3*DX3);

{определение требуемых приращений угловых координат } DB1:=(DX1*C1-DX3*S1)/(L1*C2-L2*C3); DB2:=((DX1*S1+DX3*C1)*C3+DX2*S3)/(L1*S23); DB3:=((DX1*S1+DX3*C1)*C2+DX2*S2)/(L2*S23);

{вычисление новых значений угловых координат} B1I:=B1I+DB1;

B2I:=B2I+DB2;

B3I:=B3I+DB3;

UNTIL U<10;

{ проверка требуемых ограничений на угловые координаты}

165

IF (B1I>0) AND (B1I<1.6) THEN GOTO 2 ELSE BEGIN

B1I:=1;

GOTO 1;

END;

2:IF (B2I>0.7) AND (B2I<2.4) THEN GOTO 3 ELSE BEGIN

B2I:=1.5; GOTO 1; END;

3:IF (B3I>-0.8) AND (B3I<0.8) THEN GOTO 4 ELSE BEGIN

B3I:=0;

GOTO 1;

END;

{ Вывод рассчитанных угловых координат }

4:case j of

1:begin Edit1.text:=FloatToStr(B1I); Edit2.text:=FloatToStr(B2I); Edit3.text:=FloatToStr(B3I); end;

2:begin Edit13.text:=FloatToStr(B1I); Edit14.text:=FloatToStr(B2I); Edit15.text:=FloatToStr(B3I); end;

3:begin

Edit16.text:=FloatToStr(B1I);

Edit17.text:=FloatToStr(B2I);

Edit18.text:=FloatToStr(B3I);

end;

end;

end;

166

6.5. Программная реализация алгоритма интерполяции

На практике для интерполяции траектории между опорными точками могут быть использованы полиномы различных порядков. Кубические полиномы обеспечивают непрерывность перемещений, скоростей и ускорений в опорных точках. Относительно низкая степень полинома сокращает вычислительные затраты и снижает возможность возникновения неустойчивости при вычислениях, и в то же время управляющие сигналы являются достаточно плавными. Поэтому интерполяция траектории кубическими сплайнами часто используется при контурном управлении роботом.

Определим параметры сплайна Pj,s3(t), s = 1, ..., m, из условий (3.44), (3.45), (3.46) и (3.48). Этот сплайн может быть представлен в следующем виде:

hs= ts–ts–1 – длительность временного интервала с номером s;

t – текущее время;

qj,s–1, qj,s – значения обобщенной координаты j в начале

ив конце интервала времени.

Сплайн, описываемый выражением (6.7), уже удовлетворяет условиям (3.44) и (3.46). При любых значениях Mjs его

167

ускорения непрерывны и изменяются по кусочно-линейному закону, описываемому уравнением

на отрезке времени [ts –1 , ts].

Из уравнения (6.7) следуют выражения для определения скорости изменения обобщенной координаты на s-ом и s+1-м временных интервалах

Условия непрерывности скоростей (3.45) позволяют получить из выражений (6.9), (6.10) следующее уравнение:

Условия равенства нулю скорости входного сигнала в начале и в конце траектории (3.48) дают на основе системы уравнений (6.10), (6.11) следующие уравнения для определения параметров Mj0, Mj1, ..., Mjm:

168

Из выражений (6.11), (6.12) следует система линейных алгебраических уравнений с трехдиагональной матрицей

djs=6[(qj,s+1–qjs)/hs+1–(qjs–qj,s–1)/hs]/(hs+hs+1).

Для решения системы уравнений (6.13) может быть использован метод прогонки [26]. Согласно этому методу сначала по рекуррентным формулам находятся значения вспомогательных коэффициентов es, bjs:

Затем по найденным es, bjs последовательно определяются значения параметров Mjm, Mj,m–1, ..., Mj0:

Mjm= bjm, Mjs= es M j,s+1+bjs, s = m – 1, ..., 0. (6.16)

Для расчета параметров Mjs в среде DELPHI 5.0 разработана программа 2. Ее алгоритм приведен на рис. 6.9.

169