Методическое пособие 659

Обозначим через V1, V2, V3 и V абсолютные (в декартовой системе) значения скоростей движения точек, в которых сосредоточены массы m1, m2, m3 и m. Выражения для соответствующих кинетических энергий будут иметь вид

W1 = m1V12/2 = m1 x12/2,

W2 = m2V22/2 = m2 ( x12 + x22)/2,

W3 = m3V32/2 = m3 ( x12 + x22 + x 32)/2,

(1.9)

Wm = m V32/2 = m ( x12 + x22 + x 32)/2.

С учетом (1.9) кинетическая энергия исполнительного механизма

Потенциальная энергия П(x3) системы зависит только от переменной x3, и ее частные производные имеют вид

С учетом (1.11) и (1.12) из (1.8) находим уравнения динамики трехкоординатного манипулятора с декартовой системой координат:

10

Как видно из (1.13), взаимосвязь движений по координатам x1, x2 и x3 отсутствует.

тогда из (1.13) найдем выражения, соответствующие уравне-

нию (1.7):

Уравнения (1.15) можно представить в векторной форме

где A – диагональная матрица инерционных параметров; q – матрица ускорений обобщенных координат;

C – матрица гравитационных сил;

P – матрица обобщенных сил.

Матрицы A, q, C и P имеют следующий вид:

1.4. Уравнения движения манипулятора в цилиндрической системе координат

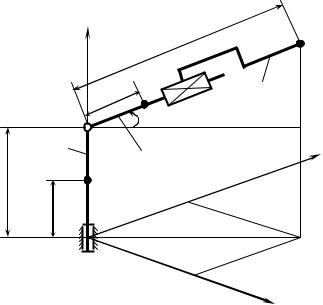
Расчетная схема манипулятора представлена на рис. 1.2. Обозначим через J1 момент инерции звена 1 относительно оси Ox3, массы звеньев 2, 3 и рабочего органа – m2, m3 и m соответственно. Геометрические размеры конструкции указаны на чертеже. Рассматриваемый трехкоординатный манипулятор имеет одну вращательную и две поступательные кинематические пары. Обобщенными координатами являются угол

поворота , высота подъема стрелы l и ее длина r.

11

C учетом (1.18), (1.19) и (1.22) кинетическая энергия исполнительного механизма определяется из выражения

Потенциальная энергия П системы зависит только от переменной l:

П(l) = m1gx2*+m2(l – l0)g + (m3+m)gl, (1.24)

где m1, x2* – масса и положение центра масс звена 1. Обозначим через М момент в сочленении координаты

, через Fl, Fr обозначим силы, действующие в сочленениях поступательного типа. Уравнения Лагранжа будут иметь вид

13

Производные от кинетической и потенциальной энергии:

Из (1.25) и (1.26) находим уравнения динамики трехкоординатного манипулятора:

Первое и третье уравнения системы (1.27) взаимосвяза-

ны, что свидетельствует о взаимовлиянии движений по углу и вдоль направления r.

Введем следующие обозначения:

C учетом (1.28) уравнения динамики трехкоординатного манипулятора в цилиндрических координатах приобретают вид

14

Векторная форма записи уравнений (1.29) имеет вид

где A(q), q – матрицы инерционных параметров и ускорений; B(q,q) –вектор, учитывающий взаимовлияние координат;

C(q) – вектор гравитационных сил; P – вектор обобщенных сил.

Обобщенными координатами для данного манипулятора

являются угол поворота стойки , высота подъема стрелы l и ее длина r.

Матрицы, входящие в уравнение (1.30), имеют вид

В отличие от уравнения (1.16), в выражении (1.30) имеется матрица B(q,q ), обусловленная взаимовлиянием вращатель-

ного движения по координате и поступательного перемеще-

ния вдоль направления r. На движение по координате оказывают влияние как величина, так и скорость перемещения по r; и наоборот, движение по координате r зависит от угловой скорости вращения руки манипулятора. Взаимовлияние

движений проявляется также и в том, что в матрице A(q) по-

явился функциональный коэффициент A (r) вследствие того, что при перемещении вдоль координаты r изменяется момент инерции относительно оси вращения Ox3. В то же время матрица A(q) остается диагональной, что свидетельствует об отсутствии влияния ускорения при движении по какой-либо координате на движение по двум другим координатам.

15

1.5.Уравнения движения манипулятора

всферической системе координат

Расчетная схема манипулятора показана на рис. 1.3. Звено 1 имеет массу m1 и момент инерции J1 относительно оси вращения Ox2. Через m2 и m обозначена масса звена 2 и рабочего органа. Манипулятор имеет две вращательные и одну поступательную кинематические пары. Обобщенными коорди-

натами являются углы поворота 1, 2 и длина стрелы r.

Рис. 1.3. Расчетная схема трехкоординатного манипулятора в сферических координатах

Уравнения Лагранжа в данном случае имеют вид

16

где M i, Fr – моменты и сила, развиваемые электроприводами. Звено 1 участвует только во вращательном движении, поэтому его кинетическая энергия определяется из выражения

Звенья 2 и 3 совершают сложные движения. Обозначим через V2 и V абсолютные значения скоростей точек m2 и m. Тогда для кинетической энергии второго звена и груза имеем

Квадрат скорости точки m2 равен

V22 =х122 +х222 +х322 = r02( 12 cos2 2+ 22 ). (1.37)

Координаты xs точки m:

17

С учетом выражений для xs находим

Выражение для потенциальной энергии П системы:

П(r, 2 )=m1gl1+m2g(r0sin 2+l)+mg(rsin 2+l). (1.43) B соответствии с (1.42) справедливы равенства:

W / 1 = 0,

W / 2 = –[(m2r02+mr2)sin 2 2 12 ] /2,

18

Уравнения системы (1.46) взаимосвязаны. Движение исполнительного механизма по какой-либо координате оказывает влияние на движение по двум другим.

Введем следующие обозначения:

Векторная форма записи уравнений динамики манипулятора в сферических координатах имеет вид (1.30), где матрицы A(q), q, P, B(q,q) и C(q) определяются следующим образом:

19