
Методическое пособие 659
.pdfz = z(t) – n-мерный вектор дополнительных (сигнальных) воздействий.
Матрица Кн вводится для обеспечения параметрической настройки, вектор z – сигнальной настройки. Кн и z являются средствами адаптации.
Предполагаем, что переменные Kн, z и g ограничены,
т. е. Kн Ок; z Oz; g Og, где Oк, Oz, Og – некоторые ограниченные множества. Тогда U Оu и управление является до-
пустимым.
Пусть задано некоторое число ео > 0 и программное движение yм(t) системы (5.1) и (5.3), удовлетворяющее уравнению эталонной модели
yм = Aм yм + Bм g, |
yм (tо) = yмо, |
(5.4) |
|
|
|
где Ам, Вм – гурвицевы матрицы (устойчивые); |
пер- |
|
yм, ум – функция состояний эталонной системы и е |
||
|
|
|
вая производная по времени.
Задача формулируется следующим образом.
Требуется построить такой закон управления U(t), чтобы при любых O , y(tо), yм(tо) выполнялось неравенство
[ y(t) – yм(t)] = [ec(t)] ≤ eo |
(5.5) |
для любых t ta, ta = tо + ta', tо 0 (где ta' – время адаптации), или предельное соотношение
lim |
[ec(t)] = 0. |
(5.6) |
t |
|
|
5.3. Адаптивное управление в рамках структуры АСЭМ
Объект опишем в следующем виде:
y |
= [At + aн(y, )]y + [Bt + bн(y, )]U + fв, |
(5.7) |
где At = At ( ), Bt = Bt ( ) – функциональные матрицы, зависящие от изменяющихся параметров ;
aн(y, ), bн(y, ) – некоторые нелинейные добавки.
120
Адаптивный регулятор (5.3) будем выполнять в виде
U(t) = Ka y + Kb(g + z), |
(5.8) |
где Кa, Кb – (n m), (n n)-мерные матрицы настраиваемых коэффициентов.
Из уравнений (5.4), (5.7), (5.8) получим выражение y = Aм y + Bм g + [At + BtKa – Aм]y + [BtKb – Bм]g +
+ fв + (aн + bн Kа)y + bнKbg + BtKbz + bнKbz. (5.9)
Из уравнения (5.9) следует, что эталонное движение (5.4) обеспечивается в том случае, если выполняются соотношения
lim ( At + BtKa) = Aм, |
lim BtKb = Bм, |
|
t |
t |
(5.10) |
fв + (aн + bн Kа)y + bнKbg + BtKbz + bнKbz = 0. |
||
В ходе адаптации Кa Кa0, Kb Kb0, где Кa0 и Kb0 со- |
||
гласно (5.10) можно определить из соотношений |
|
|
Ka0 = (Aм – At)/Bt, |
Kb0= Bм /Bt. |
(5.11) |
Введем следующие обозначения: |
|
|
Кa – Кa0 = a, |
Kb – Kb0 = b, |
(5.12) |
тогда уравнение (5.9) с учетом (5.11) запишется в виде |
|
|
y = Aм y + Bм g + Bt a y + Bt bg + fв + |
|
|
|
|
|
+ (aн + bн Kа)y + bнKbg + BtKbz + bнKbz. |
(5.13) |
|
Из (5.13) и (5.4) следует уравнение ошибки |
|
|
|
|
|
ec = Aм ec + Bt a y + Bt bg + fв + |
|
|
+ (aн + bн Kа)y + bнKbg + BtKbz + bнKbz. |
(5.14) |
|
Уравнения алгоритмов адаптации, реализующих достижение цели управления (5.10), задаются следующим образом:
121
Kн = = A1(Kн, eс, g), Kн = [Kа; Kb], |
= [ a, b], (5.15) |
|
|
|
|
|
z = A2(ec, g, , t). |
(5.16) |
Система уравнений (5.15) соответствует параметрической настройке, уравнение (5.16) – сигнальной настройке. Использование одного алгоритма параметрической настройки целесообразно, когда отсутствуют нелинейные добавки aн и
bн, а параметры изменяются в широких пределах. При нали-
чии нелинейных добавок aн, bн и изменении в узких пределах можно ограничиться сигнальной настройкой.
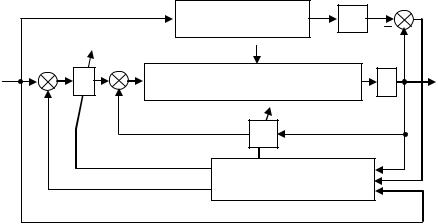
Структурная схема АСЭМ с параметрической и сигнальной настройкой приведена на рис. 5.1. Эталонное движение yм формируется в соответствии с программным управлением g согласно уравнению (5.4). Алгоритмы адаптации вырабатывают сигнал z, а также обеспечивают настройку матриц Kа, Kb по задающему воздействию g, функции состояния объекта y, а также результату сравнения eс функций состояний объекта y и эталонной модели yм. Управляющее воздействие на объект U формируется в соответствии с уравнением (5.8).
|
|
|
|
|
у |
м |
Pл |
yм |
ес |
|
|
|
ум = Aм ум +Вм g |
|
|
|
|
||
g |
|
U |
|
fв |
|
|
|
|
y |
|
|
|
|
|
|
||||
Кb |
|
|
|
|
у |
Pл |
|||
|
|
у=[At+aн] y+[Bt+bн] U+fв |
|
||||||
|
|
|
|
Кa |
|
|
|
|
|
|
|
|
z |
Алгоритмы адаптации |
|
|
|||
|
Рис. 5.1. Структурная схема АСЭМ с параметрической |
||||||||
|
|
|
и сигнальной настройкой |
|
|
|
|
||
122
5.4. Адаптивное управление в рамках структуры АСНМ
Пусть движение объекта описывается в виде уравнения, аналогичного (5.7). Преобразуем его следующим образом:
|
~ |
~ |
~ |
y= Aм y + BмU |
+(At – Aм) y + (Bt – Bм)U + fв+ aн y + bнU ,(5.17) |
||
|
|
yвых = Cн y, |
|
где U~ – n-мерный вектор управления. |
|
||
|
Настраиваемую модель будем формировать в виде |
||
|
~у |
= (Aм – Gн Cн) ~у + Gн Cн y + U(t), |
(5.18) |
где ~у, ~у – функция состояния настраиваемой модели и ее первая производная по времени;
Gн – матрица размера m m.
Адаптивный регулятор зададим в виде линейного блока
|
|
|
~ |
~ |
+ (Bм + |
~ |
|
~ |
~ |
(5.19) |
||
~ |
~ |
U(t) = Ka |
у |
Kb )(g + Ug ) + Bм z , |
||||||||
– (n m), (n n)-мерные матрицы самонастраивае- |
||||||||||||
где Ka , |
Kb |
|||||||||||
мых~коэффициентов; |
|
|
|
|
|
|
|
|
||||
z – n-мерный вектор сигнальных воздействий; |
|
|||||||||||
U~g – n-мерный вектор, введенный в управление U~ . |
|
|||||||||||
В соответствии с выражениями (5.17)–(5.19) уравнение |
||||||||||||
ошибки е~ имеет следующий вид: |
|
~ |
|
|
||||||||
|
~ |
у |
~ |
|
|
|
~ |
– |
~ |
|
||
|
е = |
– у = (At |
– Gн Cн)е + (At |
Aм –Ка ) у + |
|
|||||||
|
|
|
~ |
|
~ |
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
~ |
(5.20) |
||||
+ (Bt – Bм – Кb )(g + Ug ) + fв + aн y |
+ bнU |
– Bм z . |
||||||||||
При адаптивной идентификации достигается реализация |
||||||||||||
соотношений |
~ |
|
|
|
~ |
|
|
|
|
|||
|
|
lim |
At |
– Aм, |
|
= Bt – Bм, |
|
|||||
|
|
Ка = |
|
lim Кb |
(5.21) |
|||||||
|
|
t |
|
~ |
= fв |
|
t |
~ |
, |
|
||
|
|
|
Bм z |
+ aн y + bнU |
|
|
||||||
тогда справедливо уравнение |
е~ |
(t) = 0. |
|
|
|
|
||||||
|
|
|
|
|
lim |
|
|
|
(5.22) |
|||
|
|
|
|
|
t |
|
|
|
|
|
|
|
123
В результате адаптивной идентификации
~ |
~0 |
= At – Aм , |
~ |
~0 |
= Bt – Bм. |
|
Ка Ка |
Кb Кb |
|||||
Введем обозначения |
|
|
|
|||
|
~0 |
~ |
~ |
~0 |
~ |
~ |
|
Ка |
–Ка = а , |
Кb |
–Кb = b , |
||
тогда уравнение (5.20) перепишется в виде
~ |
~ |
~ ~ |
~ |
е |
= (At – Gн Cн)е |
+ а у |
+ b (g + Ug) + |
|
|
~ |
~ |
|
+ fв + aн y + bнU – Bм z . |
||
(5.23)
(5.24)
(5.25)
Достижение цели (5.22) адаптивной идентификации обеспечивается с помощью алгоритмов адаптации, имеющих следующий вид:
~ |
~ |
~ ~ |
~ ~ |
~ |
~ ~ |
~ |
~ ~ |
Кн = |
= А1(Кн ,ес ,U ), Кн = [ Ка ,Кb ], |
= [ а , b ], (5.26) |
|||||
|
|
|
~ |
~ |
~ ~ |
|
(5.27) |
|
|
|
z |
= А2 |
(ес ,U , , t). |
|
|
Алгоритм (5.26) соответствует параметрической настройке, алгоритм (5.27) – сигнальной настройке.
Из уравнения (5.17) при U~ = g + U~g с учетом (5.21) сле-
дует выражение |
|
|
~ |
~ |
|
~ |
~ |
|
|
|
|
|
~ |
~ |
(5.28) |
||||
у = Aм y + Bм g + Bм Ug |
+Ка |
у |
+ Кb U |
+ Bм z , |
|||||
|
|
|
|
|
|
|
|
|
|
откуда с учетом lim |
~у = y следует условие адаптивности |
|
|||||||
t |
|
~ |
|
~ |
|
~ |
|
|
|
~ |
+ |
~ |
|
~ |
|
(5.29) |
|||
Ug |
= –Bм |
(Ка |
у |
+ Кb U ) –z ', |
|||||
где ~z '– фильтрованная оценка сигнала ~z , осуществляемая с помощью m фильтров первого порядка с малой постоянной времени для обеспечения отсутствия разрывности реализуемой адаптивной схемы;
Bм+ = (BмтBм)–1Bмт – правая псевдообратная к Bм матрица. В уравнении ошибки (5.25) матрица At не определена
вследствие того, что она зависит от параметров манипуляционной системы. Выбор матрицы Gн осуществляется таким
124
образом, чтобы «покрыть» неустойчивость матрицы At, исхо-
дя из размаха области О .
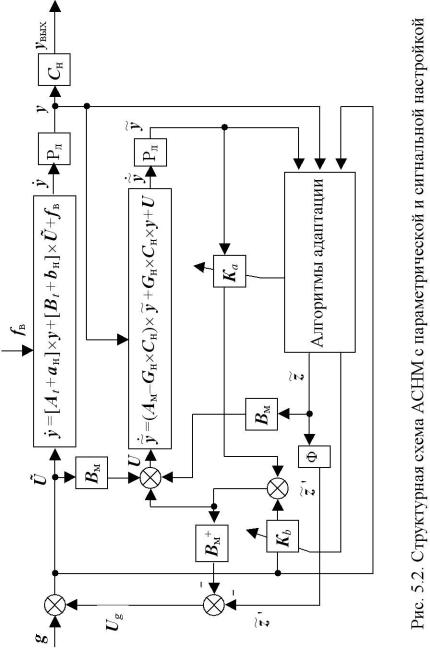
Структурная схема АСНМ приведена на рис. 5.2. На схеме представлены объект управления, описываемый уравнением (5.7), и настраиваемая модель (5.18). По результату
сравнения векторов состояний объекта y и настраиваемой мо- |
||
дели ~у, а также вектору управления |
U~ алгоритмы адаптации |
|
|
~ |
~ |
обеспечивают настройку матриц Ка и |
Кb и выработку сигнала |
|
~ |
|
|
z . Адаптивный регулятор формирует сигнал U(t) в соответ- |
||
ствии с (5.19). Сигнал U~g вырабатывается согласно (5.29). |
||
Аналогично АСЭМ |
в регуляторе вида (5.19) можно |
|
|
|
~ |
предусмотреть только параметрическую настройку ( z = 0) или |
||
~ |
~ |
|
сигнальную настройку ( Ка |
= 0, Кb = 0). С практической точки |
|
зрения особенно интересна структура по последнему варианту
слинейным законом управления.
Вследующих разделах мы рассмотрим применение рассмотренных выше принципов адаптации на примере управления двухстепенным манипулятором с электроприводами.
5.5. Математическая модель исполнительного электропривода робота
Примем, что исполнительные приводы построены так же, как большинство серийных электроприводов для роботов, по системе подчиненного регулирования. Структурная схема электропривода j-й координаты приведена на рис. 5.3.
На схеме приняты следующие условные обозначения функциональных узлов:
РПj, РCj , РТj – регуляторы положения, скорости и тока j-й координаты;
УМj – усилитель мощности j-й координаты; Мj – двигатель j-й координаты;
ДТj, ДСj, ДПj – датчики тока якоря, скорости и положения j-й координаты.
125
126
kдпj qзадj

 РПj
РПj
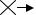 РCj
РCj
 РТj
РТj УМj Mj ДПj
УМj Mj ДПj
k |
kдтjIj |
ДТj |
ДCj |
|
|||
дсj qдj |
|
|
|
kдпj qдj |
|
|
|
Рис. 5.3. Структурная схема исполнительного электропривода одной координаты манипулятора
Значения коэффициентов передачи и постоянных времени регуляторов тока, скорости и положения выбираются в соответствии с выражениями:
Tpтj = Lj /Rj, |
kpтj = Ljωoтj /(kдтjkyjaтj), |
Tpcj = acjbcjaтj /ωoтj, kpcj = Jjkдтjωoтj /(kmjkдcjacjaтj),
Tpпj = aпjbпjacjaтj /ωoтj, kрпj = kдcjωoтj /(kдпjaпjbcjaтj), (5.30)
ωocj = ωoтj /aтj, ωoпj = ωoтj /aтjacjbcj.
В выражениях (5.30) приняты следующие обозначения:
Tpтj, Tpcj, Tpпj, kpтj, kpcj, kрпj – постоянные времени и коэффициенты передачи регуляторов тока, скорости и поло-
жения электропривода j-й координаты;
Lj, Rj – индуктивность и активное сопротивление якорной цепи двигателя j-й координаты;
kдтj, kдcj, kдпj – коэффициенты передачи датчиков обратной связи по току, скорости и положению электропривода j-й координаты;
kyj – коэффициент передачи усилителя мощности электропривода j-й координаты;
Jj – суммарный момент инерции, приведенный к валу двигателя j-й координаты;
kmj – коэффициент пропорциональности в уравнении для электромагнитного момента двигателя j-й координаты;
127
ωoтj, ωocj, ωoпj – граничные частоты пропускания контуров тока, скорости и положения привода j-й координаты;
aтj, acj, bcj, aпj, bпj – коэффициенты.
Частота ωoтj определяется требованиями помехозащищенности контура тока или малыми постоянными времени. Частоты ωoтj, ωocj, ωoпj определяют длительность, а коэффициенты aтj, acj, bcj, aпj, bпj – форму переходных процессов (перерегулирование или колебательность). Наиболее распространены два варианта значений коэффициентов:
а) при aтj = bcj = 1; acj = aпj = 2 обеспечивается настройка на переходной процесс с одним перерегулировани-
ем (4,3 %);
б) при aтj = bcj = acj = aпj = 2 происходит настройка на переходной процесс без перерегулирования.
Получим выражение для определения электромагнитного момента Мдj, развиваемого двигателем j-й координаты в схеме, приведенной на рис. 5.3. Поскольку в схеме имеется контур регулирования тока якоря, можно пренебречь влиянием обратной связи по ЭДС двигателя на динамику системы подчиненного регулирования. Такое допущение нередко используется на практике.
Физически это объясняется тем, что, как всякая замкнутая система, токовый контур стремится воспроизводить на выходе входной сигнал, которым является напряжение Uрсj c выхода регулятора скорости РСj. Изменение ЭДС, возникающее при изменении скорости двигателя, является для него возмущением и приводит к отклонению тока якоря от значения, задаваемого сигналом Uрсj. Если изменения скорости вследствие значительной электромеханической постоянной времени Тmj происходят сравнительно медленно, а быстродействие токового контура велико, то ток якоря воспроизводит сигнал Uрсj независимо от ЭДС двигателя.
Пренебрегая слагаемым, обусловленным наличием ЭДС двигателя, из второго уравнения системы (4.11) получим следующее выражение:
128
Tэ j Mд j + Мдj = Uj kmj /Rj. |
(5.31) |
Напряжение Uj на якоре двигателя определяется из структурной схемы следующим выражением:
Uj = kyjUyj = kyj{[kдпj(qзадд j – qд j )kрпj – |
|
– kдсj qд j ]kpcj – Ijkдтj}kртj, |
(5.32) |
|
|
где Uy – напряжение управления на входе усилителя мощности j-й координаты;
qзадд j, qд j – заданный и фактический углы поворота двигателя j-й координаты.
Выполним регулятор тока РТj в виде ПИ-регулятора, постоянная времени которого равна электромагнитной постоянной цепи якоря Тэм, а коэффициент передачи kртj определяется из соответствующего уравнения системы (5.30). Тогда из (5.31) и (5.32) получим уравнение
Мдj(TэjP+1) = kyj |
km j |
{[kдпj(qзаддj – qд j )kрпj – |
|
|||||||||
|
|
|
||||||||||
|
|
|
Rj |
|
|
Lj от j |
|
TэjP 1 |
|
|
||
|
– |
Мд j |
kдтj} |
|
. |
(5.33) |
||||||
|
|
|
|
|
|
|
||||||
– kдсj qд j ]kpcj |
kmj |
kдтjkyjaтj |
|
TэjP |
||||||||
|
|
|
|
|
|
|
||||||
После выполнения сокращений, преобразований, и учитывая, что малая некомпенсируемая постоянная времени контура тока Tµтj = 1/ωoтj, получим следующее выражение:
Мдj(1 + TµтjPaт) = [kдпjkрпjkpcjkmj(qзаддj – qд j ) –
– kдcjkpcjkmj qдj ]/kдтj. |
(5.34) |
|
|
Введем следующие обозначения: |
|
kпj = kдпjkрпjkpcjkmj /kдтj, kcj = kдcjkpcjkmj /kдтj. |
(5.35) |
Пренебрегая малой некомпенсируемой постоянной времени Tµтj с учетом обозначений (5.35), получим из уравнения (5.34) следующее выражение для определения момента Mдj,
129
