Методическое пособие 388

Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования

Воронежский архитектурно-строительный университет

В.С. Муштенко

ОСНОВЫ АЛГЕБРЫ И АНАЛИЗА

2 ЧАСТЬ

Курс лекций по математике

Рекомендовано в качестве учебного пособия редакционно-издательским советом Воронежского государственного архитектурно-строительного университета

для студентов, обучающихся по специальности 080502 «Экономика и управление на предприятии (строительство)»

Воронеж 2009

УДК 51.07 ББК 22.161 М34

Рецензенты:

кафедра функционального анализа и операторных уравнений Воронежского государственного университета;

Ю. С. Сербулов – д. т. н., зав. кафедрой информационных систем и технологий Воронежского института высоких технологий

Муштенко, В. С.

М34 Основы алгебры и анализа : курс лекций по математике / В.С. Муштенко; Воронеж. гос. арх.-строит. ун-т. – Воронеж, 2009.–150 с. – (Учебное пособие : в 2 ч. / В.С. Муштенко; ч. 2).

ISBN 978-5-89040-251-6

В курсе лекций приводится геометрический и экономический смысл математических понятий, математические формулировки ряда экономических законов (закона убывающей доходности, принципа убывающей предельной полезности, условия оптимальности выпуска продукции), рассматриваются простейшие приложения математики в экономике (балансовые модели, эластичность функции, производные функции, некоторые модели экономической динамики).

Основной набор примеров и задач дается в конце каждой главы в виде упражнений, которые необходимо решать на практических занятиях под руководством преподавателя или самостоятельно, при выполнении домашнего задания. В некотором смысле, материал приложений может играть роль задачника.

Предназначен для студентов, обучающихся по специальности 080502 «Экономика и управление на предприятии (строительство)».

Ил. 31. Табл. 5. Библиогр.: 10 назв.

УДК 51.07 ББК 22.161

2

ВВЕДЕНИЕ

Предлагаемое учебное пособие является продолжением первой части «Основы алгебры и анализа» для студентов экономических специальностей.

Вторая часть, соответствующая программе второго семестра, согласно общеобразовательному Государственному стандарту, содержит очень большой материал как по объему, так и по многообразию тем и разделов курса математики. Поэтому главной целью было желание оказать необходимую помощь студентам в усвоении материала, оптимально и, как можно проще изложить материал и сохранить основные разделы курса.

Имея под рукой предлагаемое пособие, студенты могут легко восполнить как пропущенные лекции, так и допущенные пробелы в своих конспектах.

К каждой главе даются приложения по теоретическим вопросам, которые являются дополнением к программе для студентов технических специальностей. Поэтому эти вопросы могут являться дополнительным материалом для самостоятельной работы студентов экономистов, а содержание всего пособия вместе с приложениями отвечает полностью программе для студентов технических специальностей.

Для основных меатематических понятий дается геометрический и экономический смысл, приводятся математические формулировки ряда экономических законов, рассматриваются простейшие приложения математики в экономике.

Основной набор примеров, задач и методов решений, а также некоторые дополнительные теоретические вопросы (доказательства некоторых теорем и выводы формул) приводятся в приложениях к каждой главе, которые при необходимости можно решать на практических занятиях под руководством преподавателя или решать самостоятельно при выполнении домашнего задания. Материал изложен максимально доступно для усвоения и сопровождается достаточным количеством примеров, которые помогут студентам лучше понять теорию и научиться применять ее на практике. Ко всем примерам и задачам приводятся ответы.

Предлагаемое пособие будет полезно студентам заочной формы обучения при самостоятельном изучении курса математики и подготовке к экзаменационной сессии, а также может быть хорошим подспорьем для преподавателей, начинающим читать курс математики студентам указанных специальностей.

Удачи на экзамене!

3

ТЕМА 1. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ Глава 1. КОМПЛЕКСНЫЕ ЧИСЛА § 1. Комплексные числа и действия над ними

Основной операцией высшей математики в разделе математического анализа является дифференцирование. Обратной операцией является действие по нахождению функции, производная которой известна, т. е. отыскание ее первообразной. Эта операция называется интегрированием. При изучении этой операции мы будем вынуждены использовать новый класс чисел – комплексные числа. С изучения таких чисел мы начнем наш курс.

1.1. Алгебраическая форма комплексных чисел

В школьном курсе элементарной математики понятие числа начинают изучать с натуральных чисел N {1,2,3,…}, но их оказывается недостаточно для

такой операции, как измерение. Поэтому были введены дробные числа mn . Це-

лые и дробные числа называются рациональными. Но положительных рациональных чисел недостаточно, чтобы вычесть большее число из меньшего. Тогда были введены отрицательные числа. Но для решения такого, например, уравне-

ния, как x 2 5 , рациональных чисел тоже оказалось недостаточно: не существует рациональных чисел, квадрат которых был бы равен пяти. Введение иррациональных чисел ликвидировало этот пробел. Решением указанного уравне-

ния являются иррациональные числа x 5.

шения не существует.

Рассмотрим еще одно уравнение: x2 4x 13 0.

D 36 , x1,2 2 36 .

Решения этого уравнения тоже не существуют.

Чтобы иметь возможность решать любое квадратное уравнение, вводят в

рассмотрение новое множество чисел.

Символ 1 называется мнимой единицей и его обозначают

где x и y R , i − мнимая единица, называется комплексным числом.

xназывается действительной частью комплексного числа и обозначается

xRe z , y называется мнимой частью комплексного числа и обозначается

yIm z ; z 0 , если x 0 и y 0 .

4

Два комплексных числа равны z1 z2 , если x1 x2 и y1 y2 ,

т. е. Re z1 Re z2 и Im z1 Im z2 .

Комплексное число z x iy называется сопряженным числу z x iy . Комплексное число, записанное в виде z x iy , называется алгебраиче-

ской формой комплексного числа.

Теперь корни квадратного уравнения x 2 4x 13 0 можно записать в виде комплексных чисел x1 2 6i , x2 2 6i .

Уравнение 3x 2 48 0 тоже имеет корни: x1,2 4i .

Таким образом, в области комплексных чисел любое квадратное уравнение всегда имеет решение, а именно два корня: либо два действительных различных, если дискриминант уравнения положителен, либо два действительных равных корня, если дискриминант равен нулю, либо два комплексных сопряжённых корня, если дискриминант отрицателен.

Над комплексными числами в алгебраической форме можно производить такие же действия, как и над действительными числами, т. е. сложение, вычитание, умножение, деление и возведение в степень:

z1 z2 (x1 x2 ) i( y1 y2 ), z1 z2 (x1 x2 ) i( y1 y2 ),

z1 z2 (x1x2 y1 y2 ) i(x1 y2 x2 y1 ),

Эти действия подчиняются тем же законам, что и действия над действительными числами.

Сопряженные числа обладают следующим свойством: их сумма и произведение есть число действительное, а разность – число чисто мнимое:

z z x2 y2 , z z.

1.2. Геометрическая форма комплексных чисел

Пусть дано комплексное число z x iy. Его можно изобразить точкой M (x, y) плоскости Oxy такой, что x Re z , y Im z.

Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Комплексное число можно задавать с помощью ра-

диус-вектора r OM (рис. 1.1).

Представление комплексного числа в виде вектора с проекциями x и y

называется геометрической формой комплексного числа. Над комплексными числами в геометрической форме можно производить те же действия, что и над

5

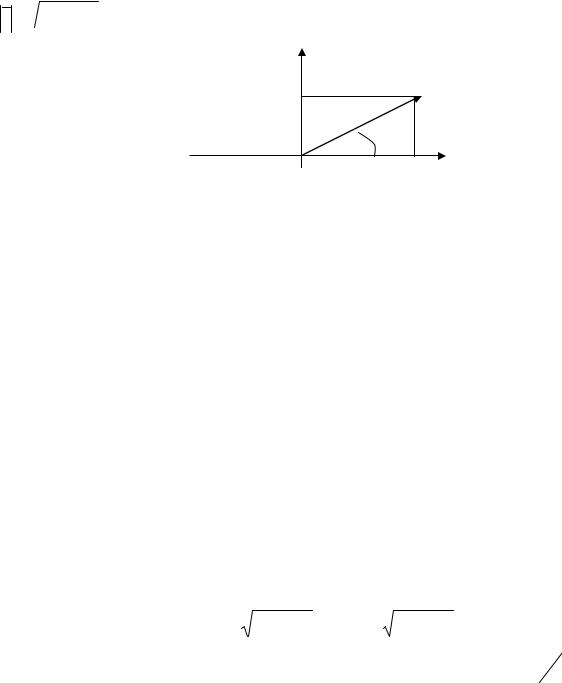
векторами: сложение, вычитание, умножение на вещественное число, поэтому комплексные числа часто истолковываются как векторы в комплексной плоскости. Модулем комплексного числа z x iy называется неотрицательное число

z = x2 y2 .

y

M (x, y)

r y

0 x x

Рис. 1.1

Аргументом комплексного числа z 0 называется угол, образованный радиус-вектором точки М с положительным направлением оси 0 x , его величина многозначна и определяется с точностью до слагаемого

2 k , k 1, 2 ,... : Argz arg z 2 k , где arg z , называемый главным значени-

ем аргумента, заключен в промежутке ( ; ]. Аргумент комплексного числа

z0 не определен.

1.3.Тригонометрическая форма комплексных чисел

Из рис. 1.1 следует

Запись комплексного числа в виде (1.4) называется тригонометрической формой комплексного числа.

Из формул (1.3) вытекает, что если arg z , то

r1r2 (cos 1 cos 2 i cos 1 sin 2 i sin 1 cos 2 sin 1 sin 2 )

r1r2[cos( 1 2 ) i sin( 1 2 )].

6

Таким образом,

r r1r2 , 1 2 , т. е. при умножении комплексных чисел их модули пере-

множаются, а аргументы складываются.

При делении, модули делятся, а аргументы вычитаются:

rr1 , 1 2 . r2

Если перемножают n одинаковых комплексных чисел, то получают степень комплексного числа

названную формулой Муавра по имени английского математика.

Эта формула позволяет вывести некоторые важные тригонометрические формулы. Положим, например, в формуле (1.6) n 3 , x.

Мы получили формулы косинуса и синуса тройного угла.

Предлагаем читателю самостоятельно получить формулы синуса и косинуса двойного угла.

Рассмотрим операцию извлечения корня степени n из комплексного числа. Определение. Корнем n ой степени из комплексного числа называется

такое комплексное число, n ая степень которого равна подкоренному числу. Пусть n z n r(cos i sin , тогда n z (cos i sin ) ;

или z n , n (cos n i sin n ) r(cos i sin ),

откуда получаем n r , n 2k , (k 0, 1, 2,...) .

Таким образом, n r n z , 2k (здесь корень арифметический).

n

Из этого следует, что для извлечения корня из комплексного числа надо извлечь корень из его модуля, а аргумент разделить на показатель корня.

При вычислении корней в качестве k достаточно брать лишь значения k 0,1,2...(n 1) , так как при больших значениях k получаются повторения уже

найденных значений корня. Окончательно имеем

7

Из формулы (1.7) следует, что корень n степени из любого комплексного числа z 0 имеет ровно n значений.

Пример 1. Найти 3 2 2i .

Решение. Имеем z 2 2i . Запишем это комплексное число в тригономет-

8

Из формул (1.9) следует, что модуль произведения двух комплексных чисел равен произведению их модулей, а аргументом произведения является сумма аргументов и что модулем частного двух комплексных чисел является отношение их модулей, а аргумент частного равен разности их аргументов.

В силу формулы Эйлера, функция ei периодическая с периодом 2 . Пример. Найти произведение и частное комплексных чисел

z1 1 i 3 , z2 1 i .

Решение. Запишем эти комплексные числа в показательной форме:

ПРИЛОЖЕНИЕ

§ 2. Разложение многочленов на множители

Рассмотрим многочлен степени n с действительными коэффициентами:

Число a (действительное или комплексное) такое, что Pn (a) 0 , называ-

ется корнем многочлена (1.10).

Из курса алгебры известно, что число a тогда и только тогда будет корнем многочлена Pn (x) , если Pn (x) делится нацело на (x a) .

Если многочлен делится на (x a)k , то a является k кратным корнем.

В теории высшей алгебры доказывается, что многочлен (1.10) степени n можно представить, и притом единственным образом, в виде

Следовательно, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действитель-

9

6.Найдите (4 7i)2 , i10 (2 2i)3 .

7.Представьте числа i , 2 , i ,1 i , 1 i в тригонометрической форме.

8.Представьте в тригонометрической и показательной формах комплексные

числа z1 2 2i, z2 1 i, z3 4i .

9. Запишите в тригонометрической форме и найдите модули комплексных чисел:

Глава 2. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

В курсе математики все ранее изученные операции встречаются попарно: сложение и вычитание, умножение и деление, возведение в степень и извлечение корня, логарифмирование и потенцирование т. е. изучается прямая операция и ее обратная. Ранее мы рассмотрели операцию дифференцирование, которая заключается в том, что для любой функции находится ее производная. Будем рассматривать задачу, обратную задаче о дифференцировании функций: пусть функция f (x) является производной некоторой функции F(x) ; требуется

найти функцию F(x) . Задачу нахождения самой функции по ее производной решает интегральное исчисление.

Ктакой математической задаче приводят многие физические, химические

идругие задачи, например, задача о разыскании закона неравномерного движения материальной точки вдоль прямой по заданной скорости, задача о нахождении закона химической реакции по известной ее скорости и другие.

10