Спектральное представление непериодических сигналов. Ряды Фурье
Метод рядов Фурье допускает определенное обобщение, позволяющее получать спектральные характеристики и непериодических сигналов. Среди них для радиотехники интерес представляют импульсные (одиночные) сигналы.
Преобразование Фурье (Fourier transform) является инструментом спектрального анализа непериодических (импульсных) сигналов (их еще называют сигналами конечной длительности, или финитными, т. е. пространственно ограниченными). Такие сигналы отличны от нуля только на ограниченном промежутке времени; иногда говорят, что сигнал существует на конечном временном интервале. Очевидно, что сигнал конечной длительности будет иметь и конечную энергию — если только он не содержит разрывов второго рода (с уходящими в бесконечность ветвями функции).
Для иллюстрации
перехода от ряда к интегральному
преобразованию Фурье применяют не
вполне строгий математически, но зато
понятный аналитический подход. В теории
спектрального представления непериодических
импульсных сигналов используют
искусственный прием, мысленно (формально)
заменяя одиночные сигналы периодическими
(как бы превращая одиночный импульсный
сигнал в виде отдельного вагончика в
бесконечный поезд, составленный из
одинаковых частей-вагончиков) с бесконечно
большим периодом следования
(рис. 11). Положим, что некоторая функция
u(t) аналитически описывает одиночный
импульсный сигнал конечной длительности
(рис. 11, а).
Мысленно дополнив
его такими же импульсными сигналами,
следующими с некоторым интервалом T
(штриховые импульсы на рис. 11, б), получим
периодическую последовательность
аналогичных импульсов
.
Для того чтобы вне искусственно введенного интервала времени 0 ... Т исходный сигнал был равен нулю, необходимо увеличить период повторения этих импульсов. В пределе, при увеличении длительности периода и , все импульсы уйдут вправо и влево в бесконечность и периодическая последовательность импульсов u(t) вновь станет одиночным импульсом u(t).
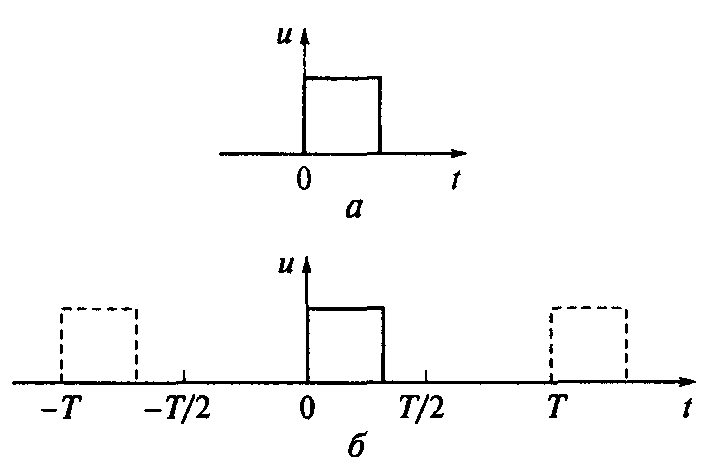
Рис. 11. Непериодические сигналы:
а — одиночный импульс; б — условное периодическое представление
При увеличении
периода следования импульсов Т гармоники
располагаются ближе друг к другу по
частоте (линейный спектр становится
все более плотным), а общий уровень
спектральных составляющих становится
все меньше. В предельном случае, когда
,
равные расстояния между спектральными
линиями уменьшатся настолько, что спектр
станет сплошным, а амплитуды отдельных
спектральных составляющих окажутся
бесконечно малыми. При этом частота
следования импульсов
и превращается в
,
дискретная переменная
— в мгновенную (текущую) частоту
,
а сумма трансформируется в интеграл.
Периодическая последовательность
импульсов
станет одиночным импульсом u(t),
и
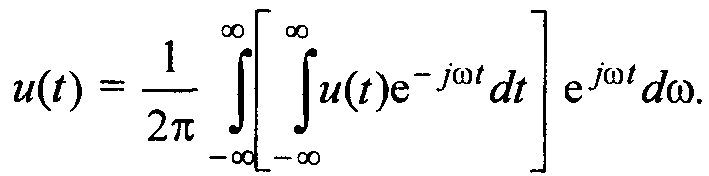(31)
Интеграл в скобках есть комплексная функция частоты. Обозначив его
(32)
получим
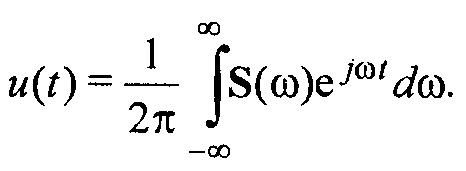(33)
Соотношения (32) и (33) носят фундаментальный характер в теории сигналов и определяют соответственно прямое и обратное преобразования Фурье (direct, inverse Fourier transform). Они связывают между собой вещественную функцию времени u(t) и комплексную функцию частоты .
Если использовать
не угловую частоту
,
а циклическую
,
то формулы прямого (32) и обратного (33)
преобразования Фурье становятся еще
более симметричными, отличаясь лишь
знаком в показателе экспоненты:
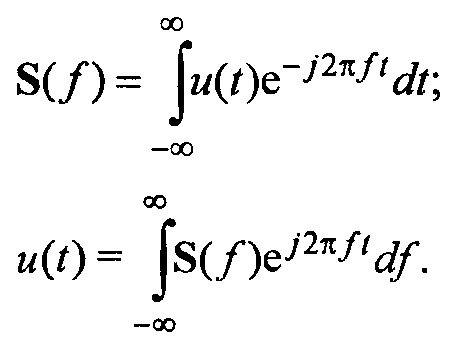(34)
Известно, что преобразования (32) и (33) существуют, если анализируемая функция u(t) удовлетворяет условиям Дирихле (по аналогии с периодическим сигналом), к которым добавляется требование абсолютной интегрируемости сигнала
(35)
Однако с привлечением
математического аппарата так называемых
обобщенных функций возможно выполнение
интегрального анализа Фурье и для ряда
сигналов, не удовлетворяющих этим
требованиям (речь идет о неинтегрируемых
сигналах). В математике под обобщенной
функцией понимают непрерывный функционал.
К таким функциям относятся, в частности,
-функция,
единичная функция и т. д.
Итак, прямое преобразование Фурье (32) ставит в соответствие сигналу, заданному во времени, его спектральную функцию. При этом осуществляется переход из временной области (time domain) в частотную область (frequency domain). Преобразование Фурье является взаимно-однозначным, поэтому представление сигнала в частотной области (спектральная функция) содержит ровно столько же информации, сколько и исходный сигнал, заданный во временной области. Принципиально важно, что спектральная плотность — комплексная функция частоты, одновременно несущая информацию, как об амплитуде, так и о фазе элементарных гармоник.
Поскольку интеграл
Фурье (32) содержит непрерывную (сплошную)
последовательность спектральных
составляющих анализируемого сигнала
с бесконечно малыми амплитудами, то
функцию
называют спектральной функцией (часто
говорят спектральная плотность (spectral
density) или просто спектр; последнее
название не совсем корректно). Она
характеризует интенсивность сплошного
распределения амплитуд гармоник
непериодического сигнала вдоль оси
частот
.
В этом основное отличие спектральной
плотности непериодического сигнала от
дискретного спектра периодического
сигнала, в котором каждая гармоническая
составляющая имеет вполне определенное
значение частоты и отстоит от соседней
на величину
.
Дискретный спектр периодического сигнала и спектральная плотность непериодического сигнала имеют разные размерности. Размерность амплитудного спектра периодического сигнала совпадает с размерностью самого сигнала — [В] или [А], а размерность спектральной плотности амплитуд определяется отношением размерности сигнала к размерности частоты — [В/Гц] или [А/Гц].
Поскольку анализируемый непериодический сигнал u(t) и его спектральная плотность взаимно-однозначно связаны прямым и обратным преобразованиями Фурье, то последние позволяют аналитически отыскать спектральную плотность по заданной форме сигнала, и наоборот, его форму по полученной спектральной плотности.