4. Представление сигналов динамическими моделями

Применяют два способа динамического представления сигналов (рис. 7).

Согласно первому — в качестве элементарных сигналов используют ступенчатые функции, возникающие через равные интервалы времени (рис. 7, а).

Высота каждой ступеньки равна приращению сигнала на интервале . При втором способе представления элементарными сигналами служат прямоугольные импульсы длительностью . Импульсы примыкают друг к другу и образуют последовательность, вписанную в кривую или описанную вокруг нее (рис. 7, б).

Р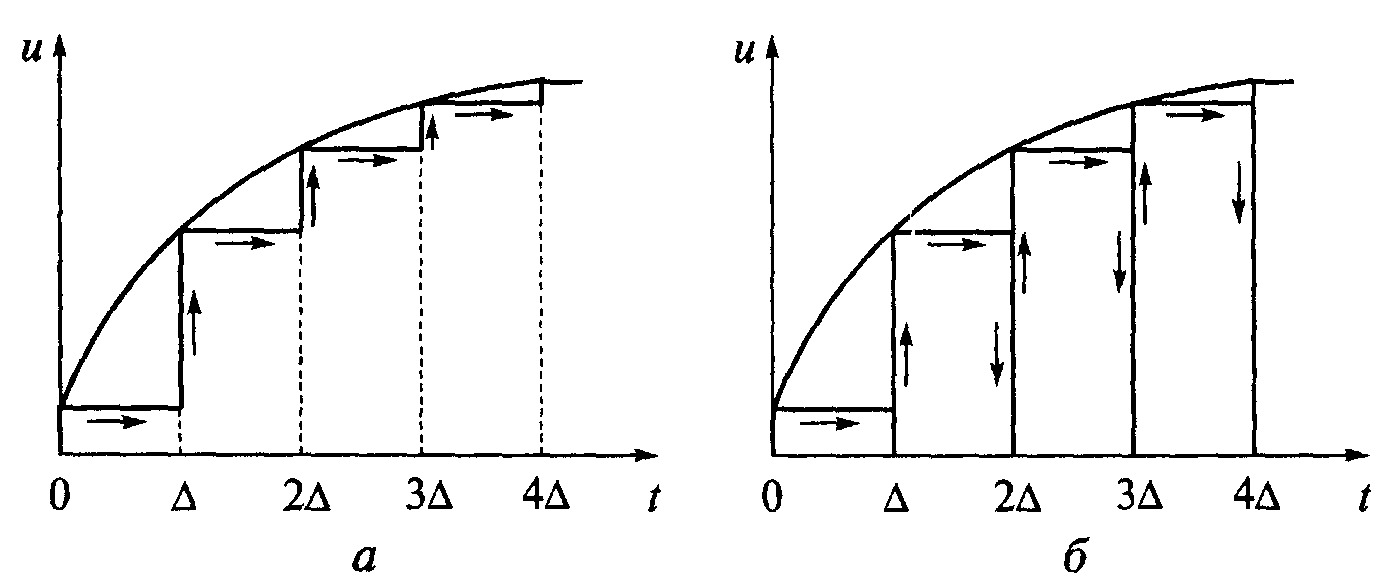 ис. 7. Способы динамического представления сигналов:

а — ступенчатыми функциями; б — прямоугольными импульсами (стрелками показаны направления изменения во времени элементарных слагаемых)

5. Энергетические характеристики сигналов

На практике одной из важных составляющих анализа сигналов является измерение их количественных параметров. Наиболее часто специалистами используются такие параметры радиотехнического сигнала, как энергия и средняя мощность (и связанное с ней среднее квадратическое значение).

Для сигнала u(t) среднее квадратическое значение (root mean square — RMS) определяется как корень квадратный из среднего квадрата его мгновенного значения (корень квадратный из средней мощности) за интервал времени

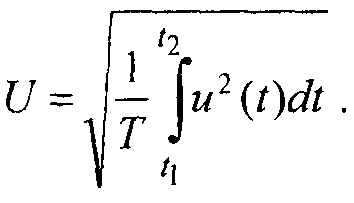(21)

Во все формулы, определяющие энергетические параметры сигнала, должно входить сопротивление нагрузки R.

Однако, если энергия и мощность интересуют нас не как физические величины, а как средство сравнения различных сигналов, этот параметр можно из формул исключить (т. е. принять сопротивление R = 1 Ом). Тогда получим определения энергии и средней мощности, принятые в теории сигналов.

Энергия сигнала u(t) [ ] за интервал времени (это квадрат нормы сигнала)

(22)

Именно такая энергия выделяется на резисторе с сопротивлением 1 Ом, если на его зажимы подано напряжение u(t).

Средняя мощность (averagepower) сигнала [ ] на том же интервал времени:

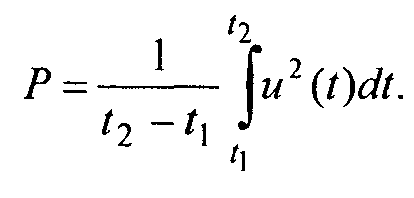(23)

Для периодического сигнала с периодом средняя мощность:

(24)

5. Спектральное представление периодических сигналов. Ряды Фурье

Фундаментальная идея спектрального представления сигналов (функций) восходит к временам более чем 200-летней давности и принадлежит знаменитому французскому физику и математику Жану Б. Фурье (Jean Б. Fourier; 1768-1830). Рассмотрим системы элементарных ортогональных функций (сигналов), каждая из которых получается из одной исходной — функции-прототипа.

Эта функция-прототип выполняет роль «строительного блока», а искомая аппроксимация получается соответствующим комбинированием одинаковых по структуре блоков. При этом если «хорошая» аппроксимация получается при использовании небольшого числа блоков, то достигается значительное сжатие информации. Ж. Фурье удалось доказать оригинальную теорему, которая в буквальном смысле ошеломила его скептически настроенных оппонентов, включая видных математиков и физиков того времени: П. Лапласа (P. Laplace), Ж. Био (J. Biot), С. Пуассона, Леонарда Эйлера (Leonard Euler; 1707-1783; знаменитый швейцарский математик) и др. Фурье свел единую функцию, трудно поддающуюся математическому описанию, к более удобным в обращении рядам гармонических тригонометрических функций, которые в сумме дают исходную функцию. Фурье показал, что любую сложную функцию можно представить (аппроксимировать) в виде конечной или бесконечной суммы ряда кратных гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Этой функцией может быть, в частности, ток или напряжение в цепи.

Солнечный луч, разложенный призмой на спектр цветов, представляет физический аналог математических преобразований Фурье (рис. 8). Свет, выходящий из призмы, разделен в пространстве на отдельные «чистые» цвета, или частоты. В спектре имеется средняя амплитуда на каждой частоте. Таким образом, функция интенсивности от времени трансформировалась в функцию амплитуды в зависимости от частоты.

Столь простое и наглядное представление сложного изменения во времени какой-либо физической величины в виде суммы ряда простейших гармонических колебаний могло показаться, на первый взгляд, лишь математическим трюком. Но это не трюк. Простой пример иллюстраций рассуждений Фурье показан на рис. 9. Периодическая, достаточно сложная по форме кривая (рис. 9, а), — это сумма двух гармоник разных, но кратных частот: первой (рис. 9, б) и удвоенной (рис. 9, в).

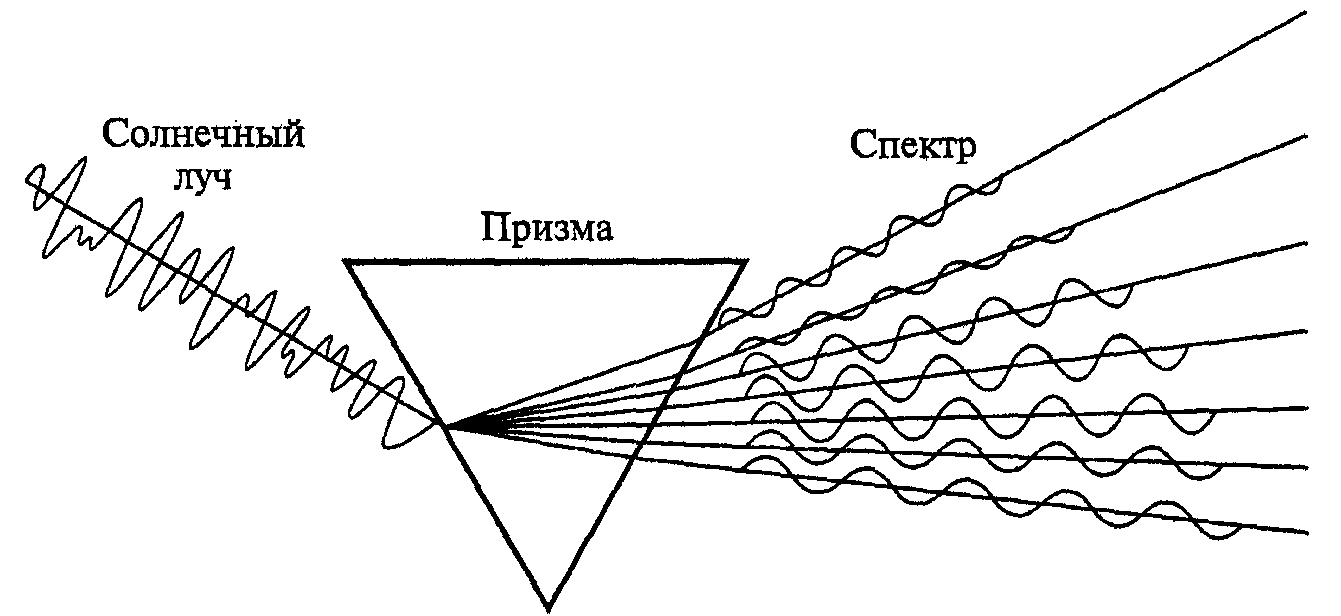
Рис. 8. Разложение света на «цвета»

При помощи анализа Фурье сложная функция представляется суммой гармонических составляющих, каждая из которых имеет свою частоту, амплитуду и начальную фазу. Преобразование Фурье определяет функции, представляющие амплитуду и фазу гармонических составляющих, соответствующие конкретной частоте (напомним, что амплитуда сигнала представляет модуль наибольшего его отклонения от нуля, следовательно, амплитуда всегда положительна, а фаза — это начальная точка синусоиды; кстати, иногда в литературе по цифровой обработке сигналов вместо термина «модуль» употребляют термин «абсолютное значение»). Преобразование можно получить двумя разными математическими методами, один из которых применяют, когда исходная функция непрерывна, а другой — когда она состоит из множества отдельных дискретных измерений. Если исследуемая функция получена из значений с определенными дискретными интервалами, то ее можно разбить на последовательный ряд синусоидальных функций с дискретными частотами — от самой низкой, основной или главной частоты, и далее с частотами, вдвое, втрое и т. д. выше (т. е. кратно превышающими) основной. Впрочем, данный ряд может содержать и постоянную составляющую. Такая сумма составляющих и называется рядом Фурье [18].

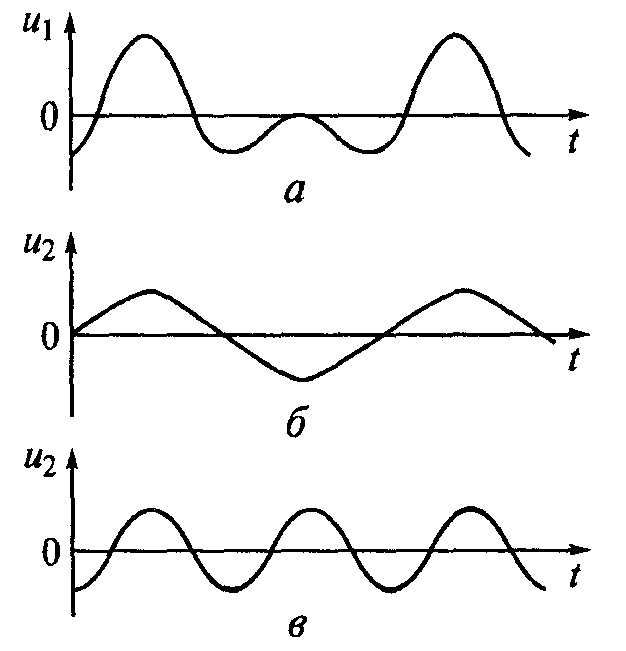
Рис. 9. К анализу Фурье:

a – сложное колебание; б,в – первый и второй аппроксимирующие сигналы

Наиболее удобным способом спектрального описания исследуемого сигнала по Фурье является его аналитическое представление с помощью системы некоторых взаимосвязанных элементарных функций времени, являющихся ортогональными. Обратимся к определениям, характеризующим основные свойства ортогональных и ортонормированных систем функций.

Пусть имеется гильбертово пространство сигналов с конечным значением энергии, определенных на конечном или бесконечном отрезке времени ( ). На этом отрезке зададим бесконечную систему (подмножество) взаимосвязанных элементарных функций времени и назовем ее базисной

(25),

Функции и ортогональны на интервале если их скалярное произведение

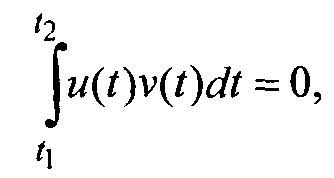(26)

при условии, что ни одна из этих функций не равна тождественно нулю.

В математике так задают в гильбертовом пространстве сигналов ортогональный координатный базис, т. е. систему ортогональных базисных функций.

Свойство ортогональности функций (сигналов) связано с интервалом их определения (рис. 10). Например, два гармонических сигнала и (т. е. с частотами и соответственно) ортогональны на любом интервале времени, длительность которого равна целому числу полупериодов (рис. 10, а). Следовательно, в первом периоде сигналы и ортогональны на интервале ; но на интервале — неортогональны. На рис. 10,б сигналы ортогональны из-за разновременности их появления.

Представление сигнала u(t) элементарными моделями существенно упрощается, если выбрана система базисных функций , обладающих свойством ортонормированности. Из математики известно, если для любой пары функций из ортогональной системы выполняется условие

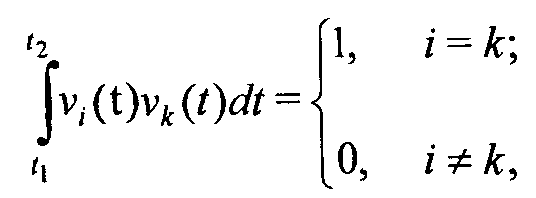(27)

то система функций, описываемая (25), ортонормированна.

В математике такую систему базисных функций вида (25) называют ортонормированным базисом.

Пусть на заданном интервале времени действует произвольный электрический сигнал u(t) и для его представления используется ортонормированная система идеализированных функций (25). Проектирование произвольного электрического сигнала u(t) на оси координатного базиса называется разложением в обобщенный ряд Фурье.

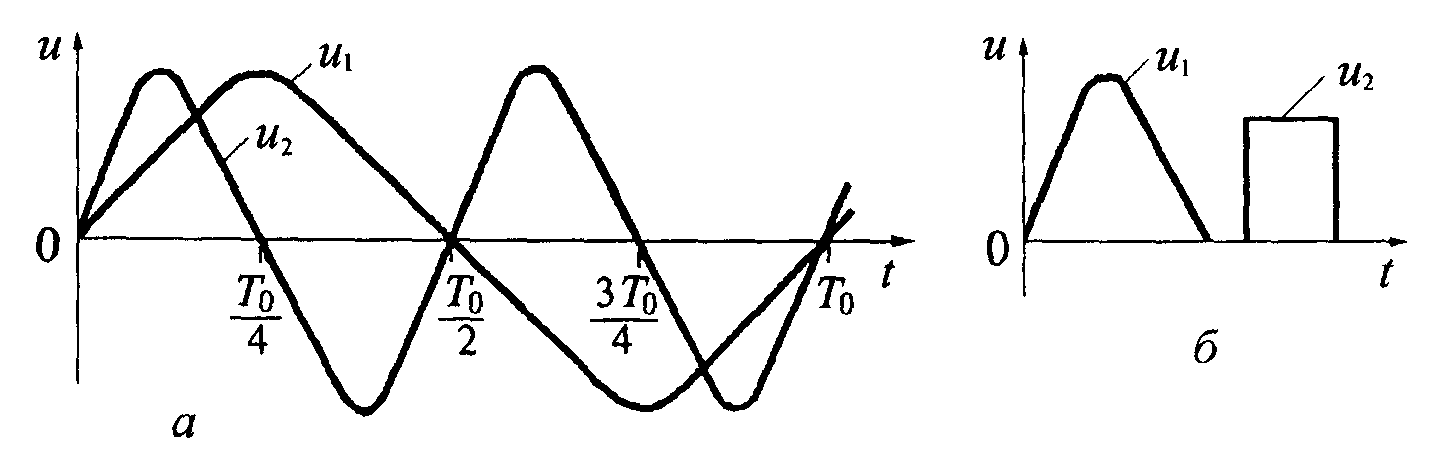
Рис. 10. Ортогональность сигналов:

а — на интервале; б — из-за разновременности появления

Это разложение имеет вид:

(28)

где — некоторые постоянные коэффициенты.

Для определения коэффициентов обобщенного ряда Фурье выберем одну из базисных функций (25) с произвольным номером к.

Умножим обе части выражения (28) на эту функцию и проинтегрируем результат по времени

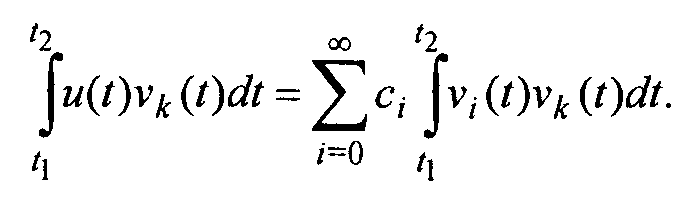(29)

Вследствие ортонормированности базиса выбранных функций в правой части этого равенства все члены суммы при обратятся в нуль. Ненулевым останется только единственный член суммы с номером , поэтому

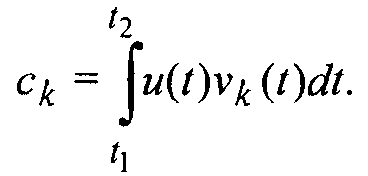(30)

Произведение вида , входящее в обобщенный ряд Фурье (29), представляет собой спектральную составляющую сигнала u(t), а совокупность коэффициентов (проекций векторов сигнала на оси координат) полностью определяет анализируемый сигнал u(t) и называется его спектром (от лат. spectrum — представление, образ).

Суть спектрального представлениия (часто анализа) сигнала состоит в определении коэффициентов (экспериментально или аналитически) в соответствии с (30). Заметим, что у относительно гладких функций спектр быстро убывает (с ростом номера коэффициенты быстро стремятся к нулю). Для относительно «изрезанных» функций спектр убывает медленно, так как для представления разрывов и «изломов» функции нужны синусоиды с большими частотами.

Достаточно распространенное использование в теории сигналов обобщенного ряда Фурье связано с его очень важным свойством: при выбранной ортонормированной системе функций и фиксированном числе слагаемых ряда (28) он обеспечивает наилучшее представление заданного сигнала u(t). Это свойство рядов Фурье широко известно.

При спектральном представлении сигналов наибольшее применение получили ортонормированные базисы тригонометрических (синусоидальных и косинусоидальных) функций. Это обусловлено следующим. Во-первых, гармонические колебания наиболее просто генерировать; гармонические сигналы инвариантны относительно преобразований, осуществляемых стационарными линейными электрическими цепями.

Гармоническое колебание теоретически полностью сохраняет форму при прохождении через любую линейную цепь с постоянными параметрами, а изменяются при этом лишь его амплитуда и начальная фаза. Во-вторых, широко используется хорошо разработанный в теории электрических цепей символический метод. Операцию представления детерминированных сигналов в виде совокупности постоянной составляющей (constant component; direct current) и суммы гармонических колебаний с кратными частотами принято называть спектральным разложением (представлением).