5.4 Изгиб цилиндрической круговой оболочки
Основные зависимости для случая изгиба замкнутой круговой цилиндрической оболочки, нагруженной равномерным радиальным давлением q (рис. 91), можно получить без использования общей теории оболочек. Считаем, что отношением толщины оболочки к радиусу кривизны можно пренебречь ввиду его малости по сравнению с единицей. В таком случае при изгибе деформации и напряжения пропорциональны расстоянию z от волокна до срединной поверхности, а при отсутствии изгиба распределяются равномерно по толщине оболочки.
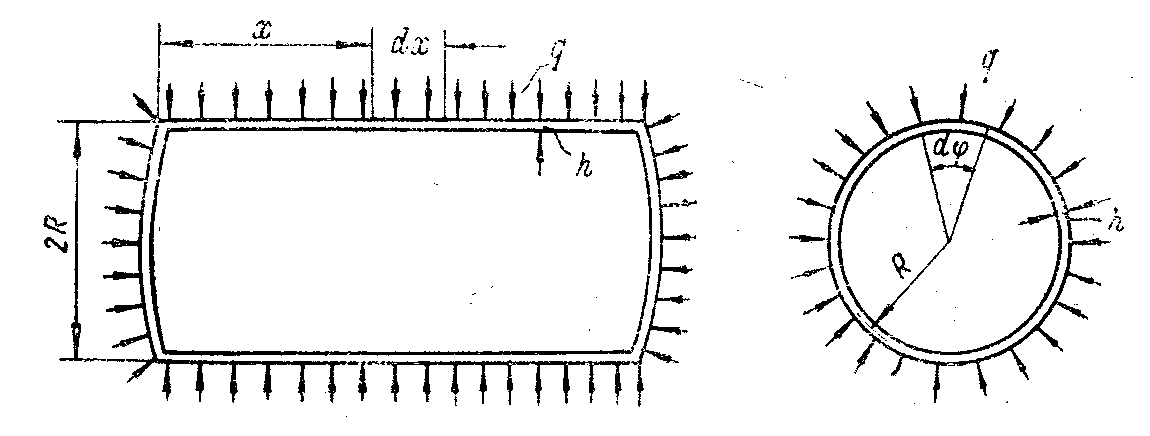
Рис. 91
Выделим из оболочки элемент двумя поперечными сечениями, находящимися на расстоянии dx друг от друга, и двумя радиальными сечениями, образующими между собой угол d. Усилия, действующие на вырезанный элемент, показаны на рис. 92.
Вследствие круговой симметрии оболочки и нагрузки относительно оси цилиндра поперечная силы Qy и крутящие моменты Н отсутствуют, а продольная сила Ny и изгибающий момент My постоянны по длине окружности. Вследствие того, что давление q нормально к срединной поверхности, сдвигающие силы Т отсутствуют. Поэтому для десяти составляющих усилий (5.1) имеем:
Рис. 92
.
Остаются лишь усилия, указанные на рис. 92, причем усилия Nу и My при переходе от одного радиального сечения к другому не получают приращения. Из шести уравнений равновесия три превращаются в тождества. Остальные три запишутся так:
(5.13)
(5.14)
(5.15)
На основании
уравнения (5.13) можно заключить, что
т. е. продольная сила Nx
постоянна. В частности, она может
равняться нулю при отсутствии у
цилиндрической оболочки торцовых днищ.
Уравнение (5.14)
после замены
,
сокращения двойки в первом члене и всех
членов на dxd
примет вид
.
(5.16)
В уравнении (5.15) второй член высшего порядка малости может быть отброшен. Тогда после сокращения на Rd dx оно примет вид:
. (5.17)
Это уравнение показывает, что установленная для стержней зависимость между поперечной силой и изгибающим моментом справедлива и в отношении к рассматриваемой оболочке. Подставив эту зависимость в формулу (5.16) и перейдя от частных производных к полным дифференциалам, ввиду того, что осталась единственная переменная х, получим
.
(5.18)
Уравнение (5.18) содержит два неизвестных: Ny и Мx, поэтому для их нахождения необходимо еще одно уравнение, которое составляется исходя из известной величины продольной силы
. (5.19)
От дифференциального уравнения (5.18) в усилиях перейдем к дифференциальному уравнению в радиальных перемещениях w. Для этого усилия выразим через деформации, а деформации через перемещения.
На основании закона Гука (1.20) при z = 0
(5.20)
. (5.21)
Приравняв правые части уравнений, найдем:
. (5.22)
Относительная окружная деформация
.
(5.23)
Подставив значения x из формулы (5.23) в (5.21), на основании формулы (5.24) получим выражение для продольной силы
,
а после раскрытия скобок
(5.25)
Изгибающие моменты, выраженные через перемещения w, определим с учетом дополнительного момента (Мх)Nx = Nw, который дает продольная сила:
.
Так как при равномерном радиальном сжатии поперечное сечение цилиндра остается круговым, радиальное перемещение w одинаково во всех точках окружности и кривизна изогнутой срединной поверхности в экваториальном направлении от изгиба
Поэтому изгибающие моменты от поперечной нагрузки q
, (5.26)
,
(5.27)
а изгибающий момент
.
(5.28)
Подставим найденные значения (5.25) и (5.28) в уравнение (5.18):
.
Группируя члены, меняя знаки, учитывая выражение (5.19) и считая, что D постоянная величина, получаем дифференциальное уравнение равновесия элемента цилиндрической оболочки в перемещениях
.
(5.29)
Продольная сила Nx влияет на величину перемещения w незначительно, поэтому, пренебрегая ею, вместо формулы (5.23) на основании (5.26) имеем
;
вместо формулы (5.25)
,
(5.30)
и вместо формулы (5.28)
. (5.31)
Тогда приближенное дифференциальное уравнение равновесия элемента цилиндрической оболочки в перемещениях
. (5.32)
В уравнении (5.31) введено обозначение
.
Величина
называется коэффициентом затухания перемещений. Она показывает, насколько затухают перемещения по мере удаления от места приложения усилия.
Расчет цилиндрической оболочки, как точный с помощью формулы (5.29), так и приближенный с помощью формулы (5.32), дает близкие результаты. Поэтому в дальнейшем будем пользоваться уравнением (5.32). Если проинтегрировать его и получить приближенное уравнение изогнутой срединной поверхности оболочки w = f (x) (без учета влияния продольной силы Nх), то все усилия и перемещения, характеризующие напряженно деформированное состояние оболочки, получатся по формуле (5.19), (5.30), (5.31) (5.27) и (5.17).
Угол наклона касательной к изогнутой срединной поверхности
.
Следует иметь в виду, что знаки в перечисленных формулах предусматривают внешнее радиальное давление q. При внутреннем давлении знаки должны быть изменены на обратные.
Интеграл дифференциального уравнения (5.32) складывается из интеграла однородного уравнения и частного решения уравнения (5.32); он может быть представлен с помощью показательных функций в виде
.
(5.33)
или, если заменить показательные функции гиперболическими на основании зависимостей
,
в виде
.
(5.34)
В выражениях (5.33) и (5.34) f(х) частное решение дифференциального уравнения (5.32). В случае радиальной нагрузки интенсивностью q, равномерно распределенной по поверхности оболочки, частное решение f(х), имеет вид
. (5.35)
При этом
,
и уравнение (5.32) при подстановке в него решения (5.35) превращается в тождество.
Коэффициенты С1, . . ., С4 и А1, . . ., А4 представляют собой произвольные постоянные, определяемые из граничных условий. Если усилия и перемещения на одном конце цилиндрической оболочки не влияют на усилия и перемещения, возникающие на другом конце, оболочка считается длинной. Если эти факторы влияют друг на друга, то оболочка считается короткой.
Если в дифференциальном уравнении (5.32) принять правую часть равной нулю (при отсутствии радиальной нагрузки q), то оно примет вид
.
(5.36)
Уравнение (5.36) представляет собой уравнение балки на упругом основании, в нем принято обозначение
, (5.37)
где k коэффициент постели, связывающий интенсивность реакции основания q с прогибом балки w:
q = -kw.
Вследствие аналогии между уравнениями (5.32) и (5.36) полоску шириной, равной единице, вырезанную из цилиндрического сосуда вдоль образующей, можно рассматривать как балку на упругом основании и использовать все решения, применяемые при расчете такой балки, для расчета цилиндрической оболочки. При этом реакция основания
,
что следует из рис. 93.
Для полоски шириной,
равной единице, центральный угол дуги
,
а сжимающие силы
.
Рис. 93
Поэтому
.
Следовательно,
и коэффициент (5.37), если заменить в его выражении жесткость балки EJ цилиндрической жесткостью D,
представляет собой коэффициент затухания перемещений.