4.7 Температурные напряжения в пластинах
В общем случае температура в какой-либо точке круглой пластины является функцией двух переменных: радиуса х и расстояния z от точки до срединной плоскости. В силу линейности основных уравнений для температурных напряжений напряжения, вызванные радиальным изменением температуры tx2 – tx1 и изменением температуры по толщине t2 – t1 можно вычислить отдельно, а затем алгебраически суммировать. Ниже рассматриваются два случая изменения температуры: 1) температура одинакова для всех точек, расположенных на одинаковом расстоянии z от срединной плоскости, но меняется по толщине пластины по прямолинейному закону; 2) температура постоянна по толщине, не зависит от полярного угла , но меняется в зависимости от расстояния х между точкой и центром пластины.
Случай
1. При одинаковом во всех точках одной
окружности изменении температуры по
толщине пластины
,
подчиняющемся прямолинейному закону
(рис. 70), перемещение этих точек пластины,
связанное с ее расширением или сжатием,
происходит также одинаково по всем
направлениям в плане.
В случае повышения температуры верхняя поверхность пластины получает большее расширение, чем нижняя, и пластина изгибается по шаровой поверхности радиусом выпуклостью вверх. На основании допущения о прямых нормалях можно считать, что относительная деформация (по отношению к срединному слою), происходящая на наружной поверхности в любом направлении,
. (4.43)
Рис. 70
С другой стороны, относительная температурная деформация отрезка длиной l на наружной поверхности по отношению к срединному слою
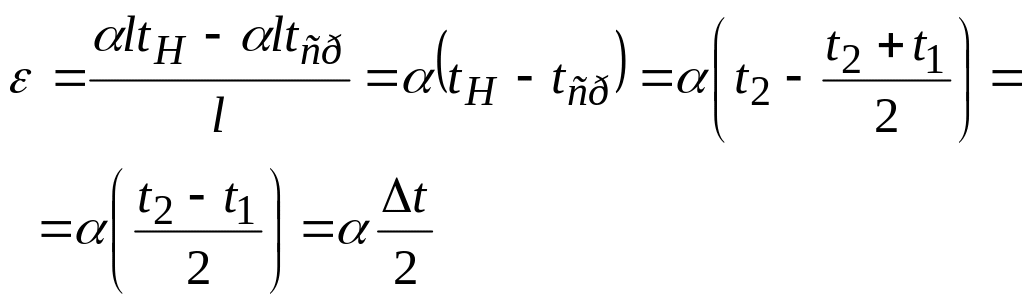. (4.44)
Приравняв выражения (4.43) и (4.44), можно получить формулу для определения кривизны шаровой изогнутой поверхности
.
(4.45)
Если круглая пластина не имеет закреплений или свободно поворачивается на контуре (свободно оперта), то температурное искривление не вызывает дополнительных усилий. Если же пластина защемлена, на контуре возникнут погонные опорные моменты Мr, уничтожающие кривизну, вызванную неравномерным нагревом.
При сферическом изгибе моментами Мr кривизна
.
(4.46)
Приравняв выражения (4.45) и (4.46), получим формулу для определения погонного изгибающего момента
,
а разделив это
выражение на момент сопротивления
и подставив вместо цилиндрической
жесткости D
ее значение из формулы (4.12), определим
наибольшее напряжение:
. (4.47)
Случай 2. Круглая пластина с центральным отверстием радиусом а подвергается действию температуры, имеющей радиальный перепад (рис. 71).
Рис. 71
В дальнейшем t(x) обозначено для краткости t. Напряженное состояние в пластине считаем плоским, т. е. полагаем z = 0. В силу симметрии условий и расчетной схемы перемещения и зависят только от радиуса х, а перемещения v равны нулю. Поэтому относительные деформации
. (4.48)
Если решить первые
два уравнения (4.48) относительно r
и Т
, а в третьем заменить rT
на
,
можно получить
. (4.49)
Подстановка
значений (4.49) в уравнение равновесия
плоской задачи в полярных координатах,
принимающее в данном случае (
= х) вид
,
приводит к следующему дифференциальному уравнению для радиального перемещения:
.
Для интегрирования этого уравнения левая его часть записывается так [см. аналогичное решение уравнения (4.36)]:
.
(4.50)
Первое и второе интегрирование (4.50) дает
. (4.51)
В выражении (4.51) через х1 обозначен переменный радиус, определяющий точки, расположенные между а и х. Если подставить это выражение в формулы (4.49), то получатся следующие выражения для температурных напряжений:
.
(4.52)
Постоянные С1 и С2 определяются из граничных условий на контурах пластины. Если отверстия радиусом а в пластине нет, то интегрирование в формулах (4.52) выполняется в пределах от нуля до х.