2.2 Деформация толстостенного сферического сосуда
При решении некоторых задач, когда многие компоненты напряжений и деформаций отсутствуют, можно не прибегать к общим уравнениям теории упругости (в перемещениях или в напряжениях), которые должны значительно упроститься, а все три необходимые стороны исследования (геометрическую, физическую и статическую) выполнить непосредственно применительно к рассматриваемому частному случаю.
Представим себе шаровой сосуд, подвергающийся действию внутреннего и внешнего равномерных давлений. Пусть а и b обозначают соответственно внутренний и наружный радиусы шара (рис. 21), а рa и рb внутреннее и наружное давления газов.
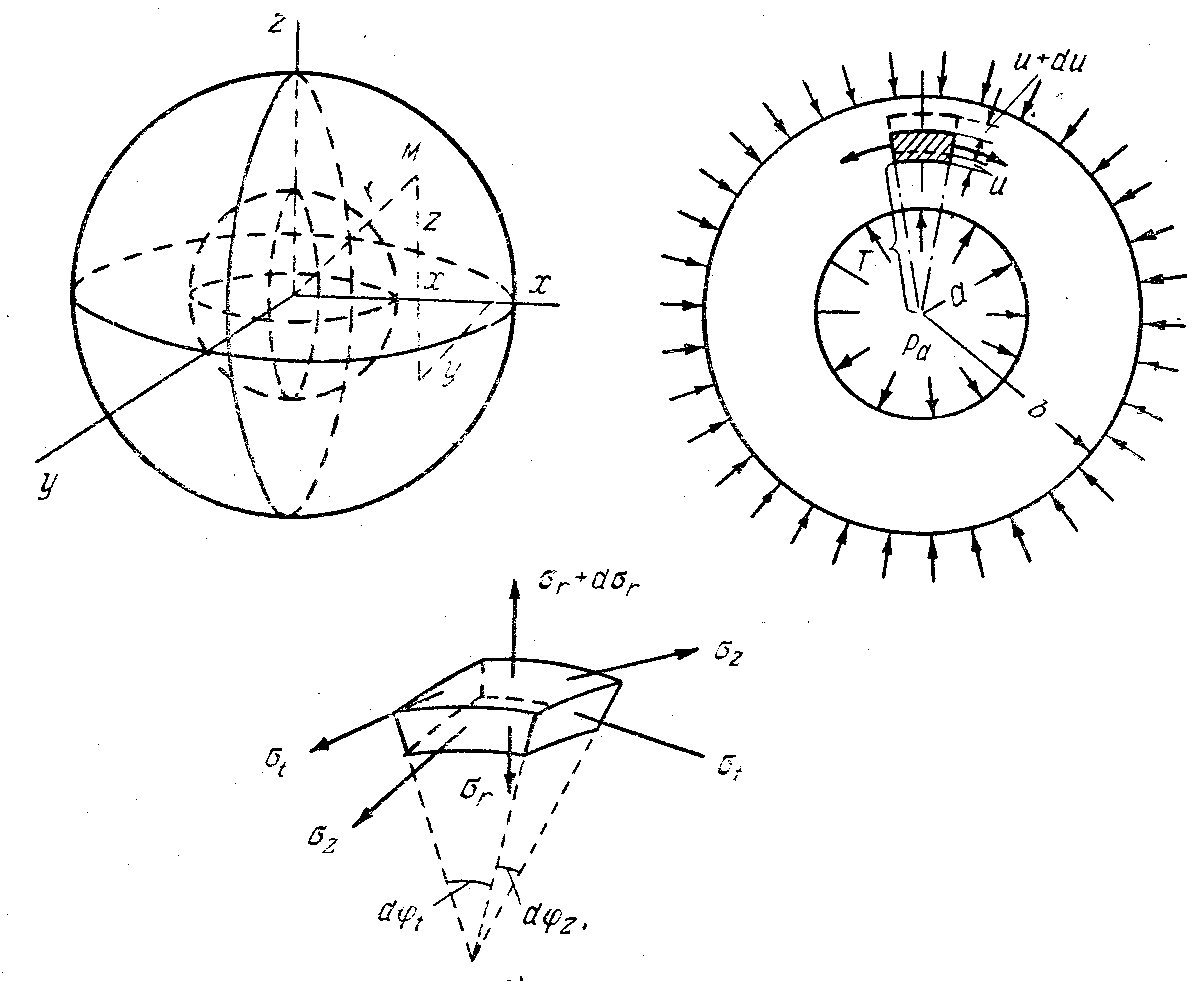
Рис. 21
Начнем со статического
обследования. Вырежем для исследования
бесконечно малый элемент двумя парами
взаимно перпендикулярных меридиональных
сечений и двумя концентрическими
сферическими поверхностями. Действие
отброшенных частей сосуда заменим
тангенциальными (t
, z)
и радиальными (r)
напряжениями. Так как в рассматриваемом
случае напряжения зависят только от
радиуса r,
то напряжения по двум бесконечно близким
друг к другу концентрическим поверхностям
будут отличаться на величину
и не будут зависеть от угла
другого параметра, определяющего
местоположение рассматриваемого
элемента. Проектируя все силы на нормаль
к элементу, имеем уравнение равновесия
в виде:
.
Имея в виду равенство t = z и производя сокращения, получаем уравнение равновесия:
.
(2.27)
Переходим к геометрическому обследованию. Из рассмотрения перемещений и формоизменения элемента заключаем, что относительное тангенциальное удлинение:
, (2.28)
а относительное радиальное удлинение:
.
(2.29)
Выполним физическое обследование. Зависимость напряжений от деформаций в данном случае имеет вид:
Напряжения через деформации выражаются (принимая во внимание равенство t = z и t = z) так:
. (2.30)
Данные геометрического обследования используем для преобразования полученных физических зависимостей, т. е. подставляем (2.28) и (2.29) в (2.30). Имеем выражения для напряжений:
(2.31)
(2.32)
Выражения (2.31) и (3.32) подставляем в уравнение статики (2.27). Тогда после сокращений получаем выражение
, (2.33)
которое представляет собой уравнение, объединяющее в себе все три стороны исследования (геометрическую, физическую и статическую).
Общий интеграл дифференциального уравнения (2.33) имеет вид
.
(2.34)
Дифференцируя (2.34), находим
. (2.35)
Подставляя (2.34) и (2.35) в (2.31) и (2.32), получаем вместо дифференциальной формы выражения для напряжений в алгебраической форме:
(2.36)
. (2.37)
Постоянные интегрирования А и В определим из поверхностных условий:
.
Тогда, в силу (2.37), имеем:
откуда
(2.38)
Подставляя (2.38) в (2.36) и (2.37), окончательно получим:
Для случая одного внутреннего давления рa наибольшее растягивающее тангенциальное напряжение будет на внутренней поверхности сосуда (при r = a):
а минимальное - на наружной поверхности (при r = b):
.
Приведенное здесь решение задачи теории упругости получено применением метода перемещений.