5.6.3. Открытая штамповка круглых в плане поковок с наметкой под прошивку

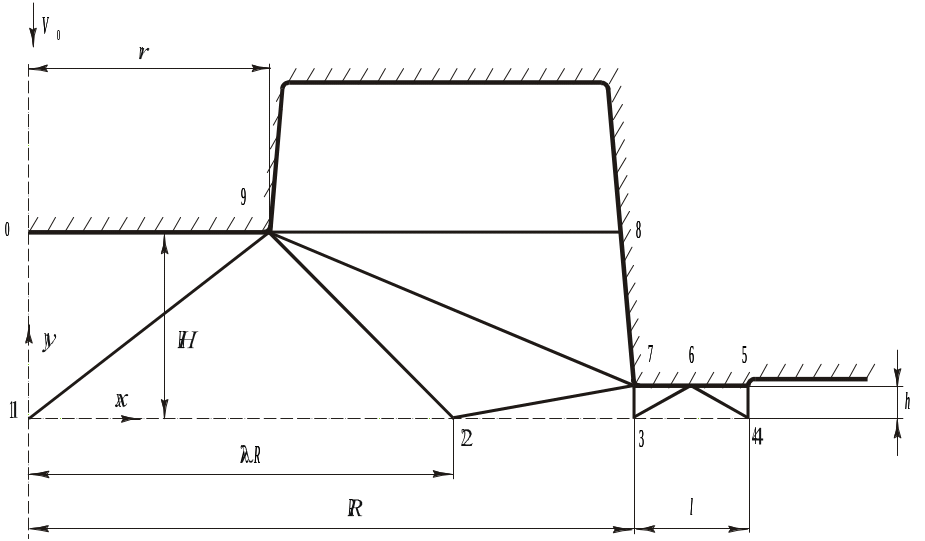
Рис. 5.8.

Здесь рассматривается заключительная стадия штамповки в предположении, что гравюра штампа заполнена и излишек металла выдавливается в заусенечную канавку. Нетрудно показать, что в этом случае на линии 9-8 разрыв скорости отсутствует, треугольник 9-7-8 движется вместе со штампом, а пластическая зона ограничена областью 0-1-2-3-4-5-6-7-9-0. Существенное влияние на решение оказывает координата точки 2, которая для удобства обозначена через , где – варьируемый параметр, 0< <1.

В таблице 5.4 приведены координаты и значения функций тока в узлах разбиения.

Таблица 5.4

№ п.п.	0	1	2	3	4	5	6	7	8	9
Xi	0	0	R	R	R+l	R+l	R+0,5l	R	R	r
Yi	H	0	0	0	0	h	h	h	H	H
Фi	0	0	0	0	0	X5V0	X6V0	RV0	RV0	rV0

Так как на линии 9-8 разрыв скорости равен нулю, то координаты точки 8 не влияют на решение задачи и для простоты будем считать

, .

Воспользовавшись формулами (5.13) и (5.11), а также приведенными в таблице (5.4) узловыми значениями , , найдем коэффициенты , в треугольниках и энерговыделение на всех линиях разрыва скорости. Так как штамповка ведется в горячем состоянии, коэффициенты , характеризующие трение на контакте с инструментом, целесообразно принять равными единице. Приведем значения коэффициентов и для функции тока в треугольнике 2-7-9

, ,

В таблице 5 приводятся формулы для расчета энерговыделения на линиях разрыва скорости и на контакте с инструментом.

Суммируя и, пренебрегая слагаемыми, дающими относительно малый вклад, получим:

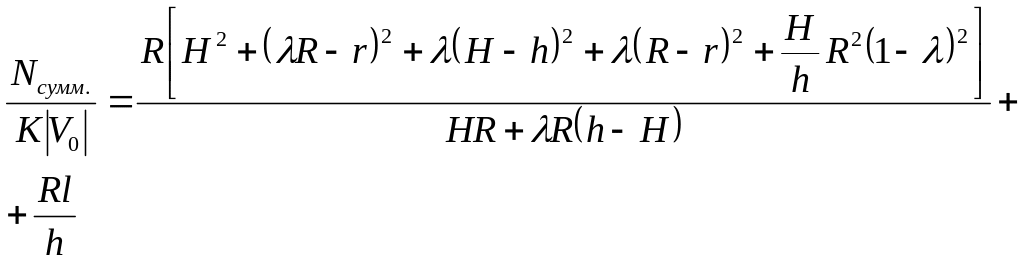(5.27)

Таблица 5.5

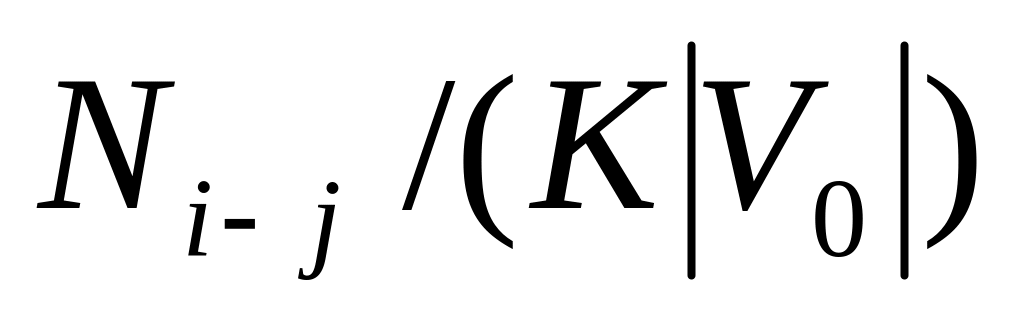
1-9
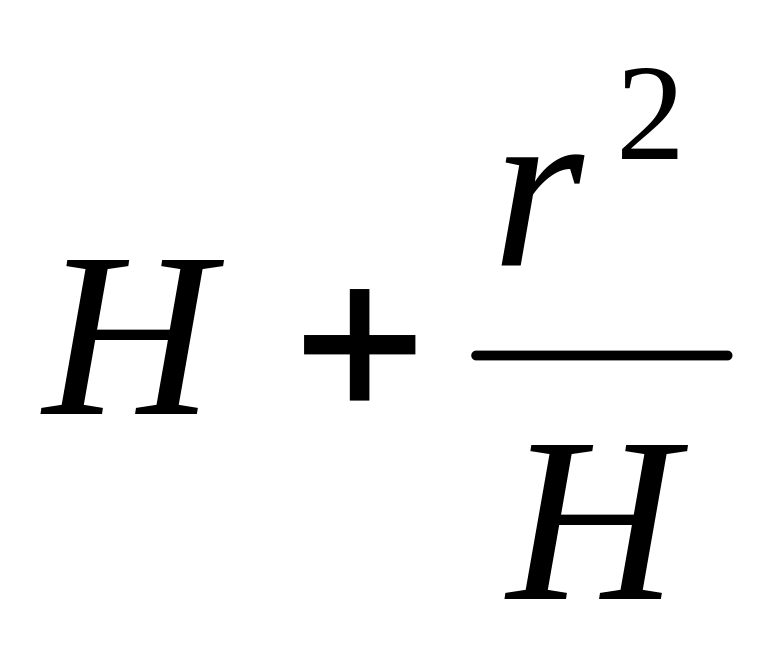
9-2
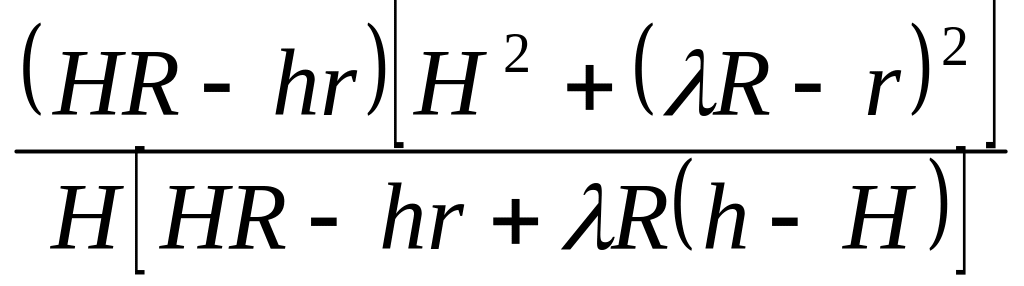
9-7
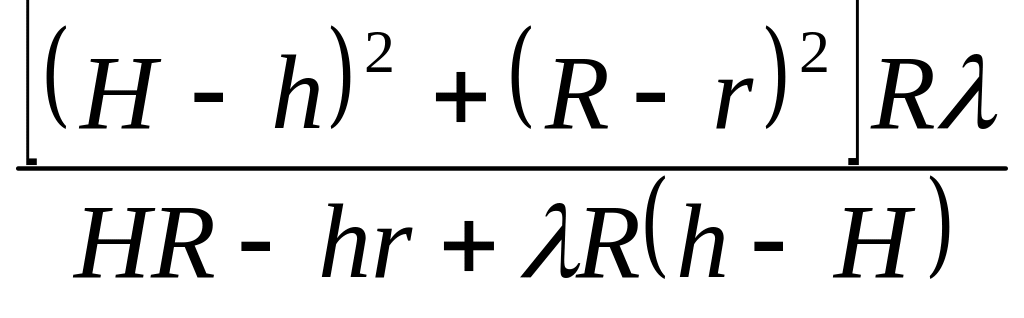
2-7
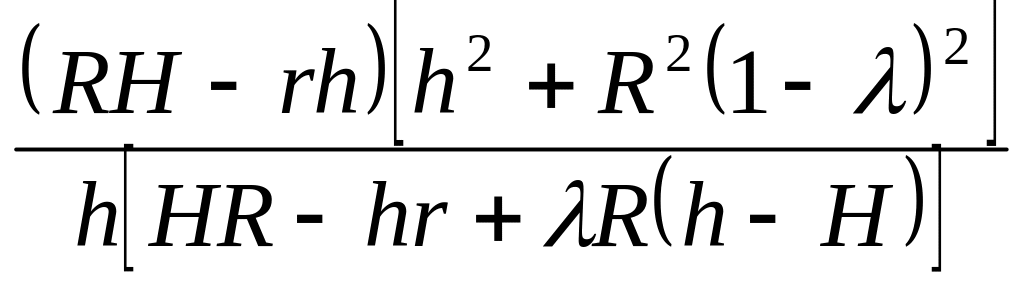
3-7
3-6, 4-6
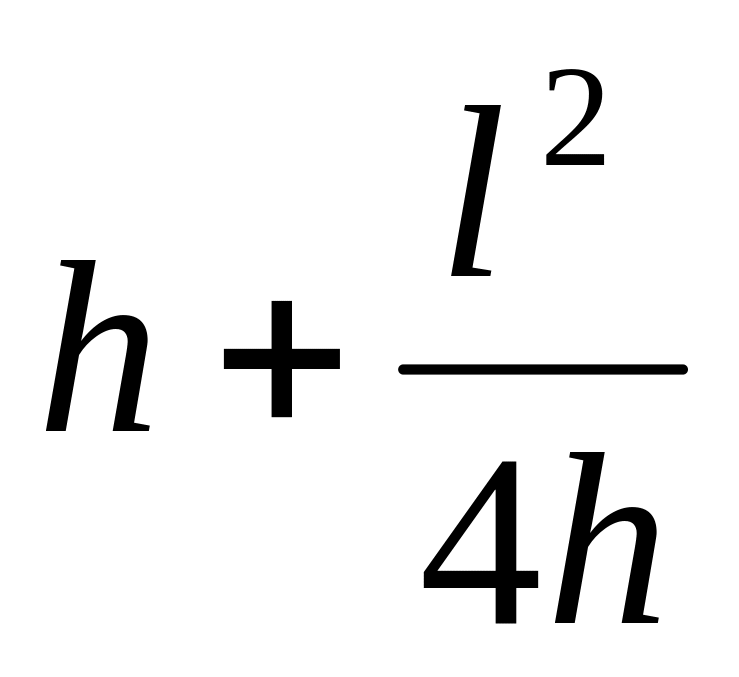
7-6
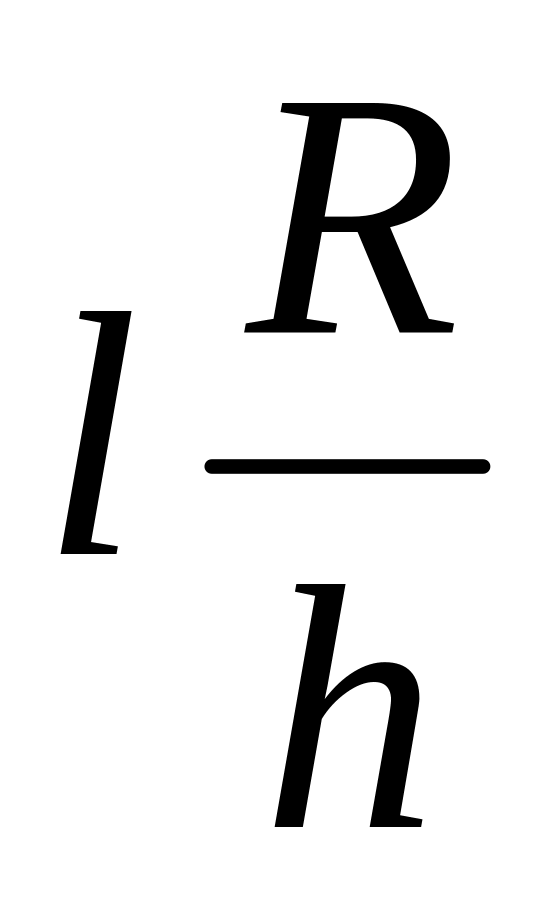
6-5

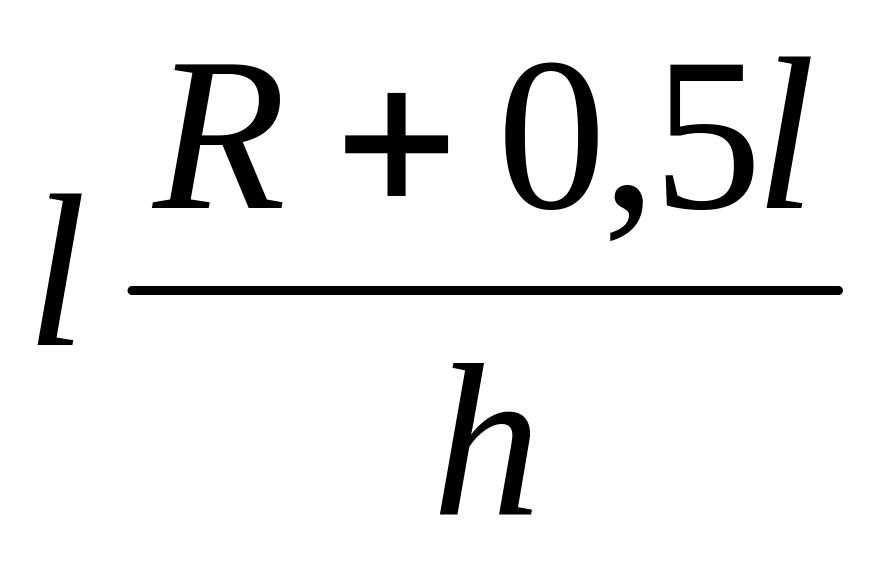
Суммируя и, пренебрегая слагаемыми, дающими относительно малый вклад, получим:

.

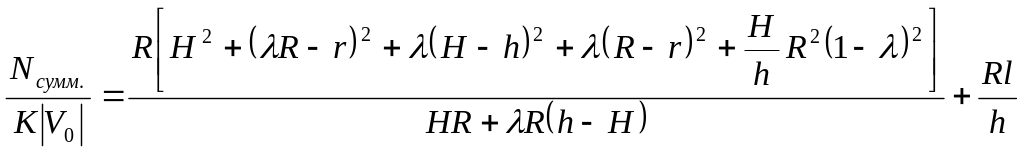Учитывая, что предел текучести и пластическая постоянная связаны соотношением , нетрудно получить формулу для расчета усилия штамповки

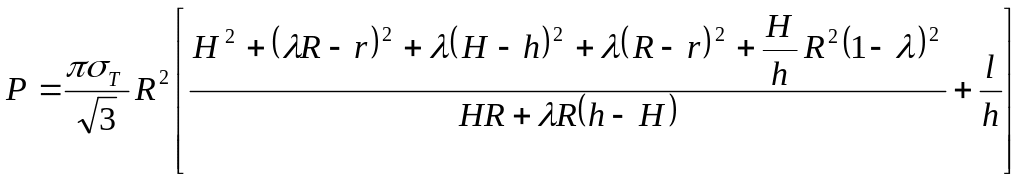(5.28)

Параметр можно определить из вариационного принципа . Не приводя преобразований, запишем окончательный результат

, (5.29)

Где , ,

, .

5.7. Расчет деформированного состояния при плоском пластическом течении

При пересечении материальной точкой линии разрыва скорости элементарный объем претерпевает некоторое изменение формы. Численной характеристикой приращения накопленной деформации является величина [2,3,16]

,

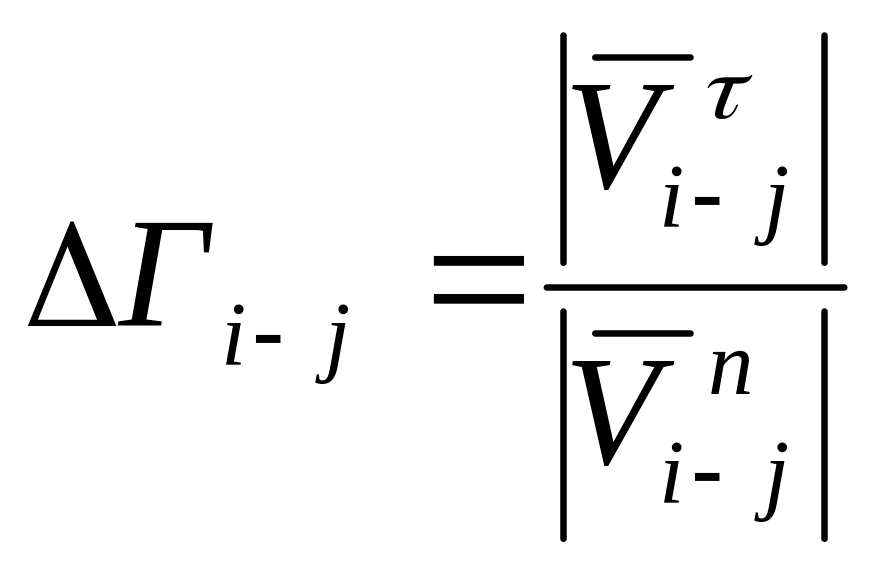где – нормальная к линии компонента вектора скорости на элементе. Отметим, что в силу условия неразрывности при пересечении линии разрыва величина вектора не меняется.

Пусть – составляющие вектора скорости в треугольнике (рис. 1). Через обозначим вектор нормальный к линии и имеющий модуль, равный . Тогда проекции вектора на оси и будут

.(5.30)

Подставляя (5.29) в (5.27), с учетом (5.11), получим

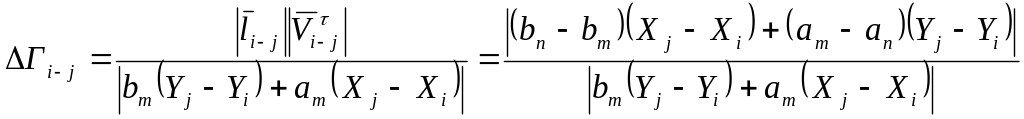.(5.31)

Заметим, что условие

(5.31)

соответствует случаю, когда вектор скорости коллинеарен . Тогда приращение деформации на линии разрыва бесконечно. Однако именно по причине параллельности линия тока не пересечет линии разрыва, а в худшем случае совпадет с ней, как это имеет место на линии тока, совпадающей с линией тока и линией разрыва скорости. Для случая редуцирования, рассмотренного в п.5.6.1

,

,

.

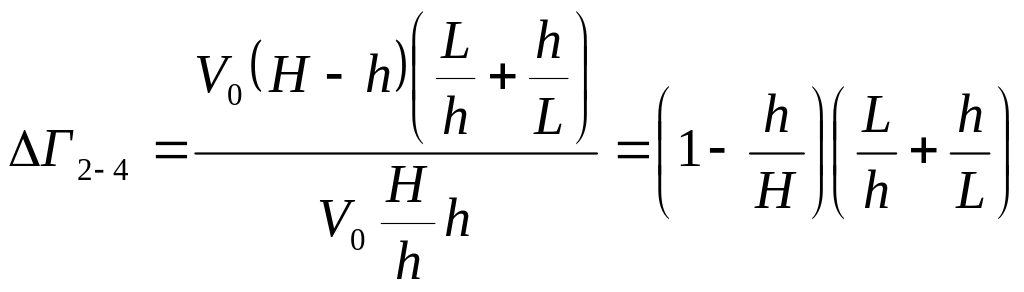Таким образом, суммарная деформация на выходе из пластической области при редуцировании равна

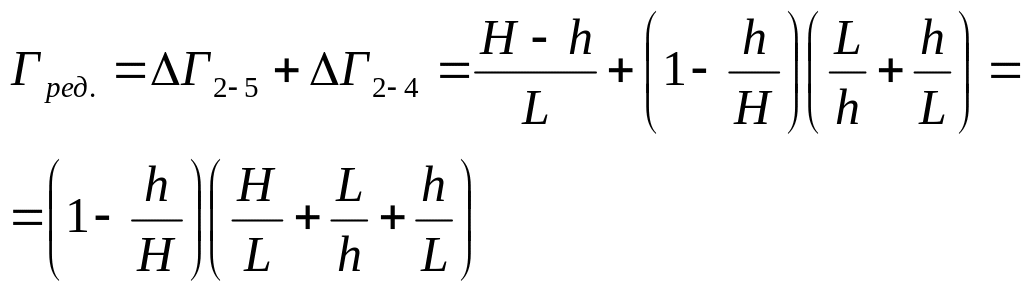(5.32)

Любопытно отметить, что для случая, рассмотренного там же,

,

,

т. е. степень деформации , как правило, численно не совпадает с накопленной деформацией . Полученное значение величины накопленной деформации используется при расчете технологических параметров с учетом деформационного упрочнения и ресурса пластичности.