4.5.1. Алгоритм решения задачи

Последовательность решения задачи можно представить:

1. На первом этапе, предполагая независимость геометрии процесса от изменения механических свойств материала и, полагая последний неупрочняемым, определим усилие деформирования (см. рис. 4.7).

(4.73)

2. Находим объем, охваченный пластической деформацией для принятой расчетной модели (здесь полагаем, что вся поковка пластически деформируется)

(4.74)

С учетом постоянства объема имеем

(4.75)

3. Определяем значение среднеинтегральной величины интенсивности скорости деформации .

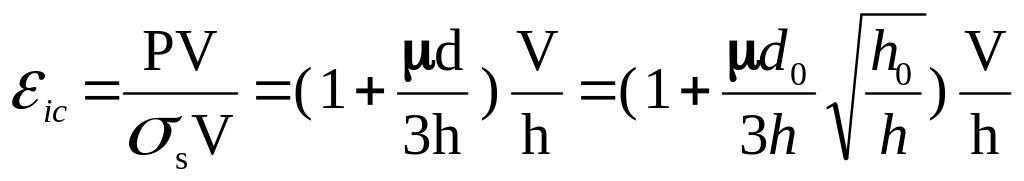; (4.76)

4. Находим величину среднеинтегральной интенсивности конечной деформации .

(4.77)

Производя замену переменной , получаем:

(4.78)

С учетом постоянства объема и равенства (4.74)

(4.79)

Производя интегрирование и преобразование, получим

(4.80)

5. Подставляя полученные выражения и в формулу (4.33) получим значение с учетом деформационного и скоростного упрочнения.

6. Пользуясь скорректированным значением подсчитываются энергосиловые параметры процесса.

Однако не всегда удается в конечном виде проинтегрировать соответствующие выражения для е_i0. В подобных случаях прибегают к следующим упрощениям:

- величины, характеризующие геометрию очага деформации, (в нашем случае это d/h) в подинтегральном выражении на данном отрезке интегрирования (от до ) считают величиной постоянной и равной некоторой величине между и .

-для более грубой оценки можно принять, что

(4.81)

где обычно

Естественно, что рассмотренные упрощения будут давать тем более точные результаты , чем более мелкие отрезки деформирования мы будем применять в расчетах.

5. Метод конечных элементов в обработке металлов давлением

5.1. O методе конечных элементов

Конечные элементы (КЭ) в плоском случае могут быть треугольными, четырехугольными, фигурами более сложной формы, например многоугольниками с криволинейными сторонами. Пробная функция в каждом КЭ определяется по значениям в определённых точках КЭ, называемых узлами. Узловые значения решения либо определяются граничными условиями, либо являются варьируемыми параметрами. Иногда можно также варьировать разбиением области.

Исходная вариационная задача сводится, следовательно, к задаче минимизации функции конечного числа переменных.

Здесь применяется следующая схема МКЭ:

1. пластическая зона разбивается на треугольные конечные элементы;

2. решение задачи в i-ом КЭ ищется в виде полинома первой степени от (x, y) – декартовых координат плоскости т.е. в виде

_{i (x,y)}=a_ix+b_iy+c_i (5.1)

3) коэффициенты a_i, b_i, c_i , по значениям _i(х,у) в узлах. Узлами являются вершины i-го треугольника.

Таким образом, решением задачи методом конечных элементов будет выбор функций вида (5.1), аппроксимирующей решение в каждой подобласти. Так как значения в общих узлах двух соседних элементов берутся одними и теми же, то полученная кусочно-полиномиальная функция будет непрерывной.