5.6. Примеры решения технологических задач обработки давлением [17]

5 .6.1. Редуцирование и волочение полосы в клиновых матрицах (рис. 5.4)

Рис. 5.4

Через и обозначим высоту полосы до и после деформирования. Разобьем предполагаемую пластическую зону на три элемента, как показано на рис. 5.4, и введем декартовую систему координат так, чтобы ось совпадала с осью заготовки. Зададим значения функции тока в узлах разбиения. Точки 1, 2, 3 лежат на оси симметрии, поэтому .

Из свойства б) линий тока имеем

,

отсюда

,

Сторона 5-4 является линией контакта, обтекаемой металлом, поэтому – линия тока. Так как вдоль линии тока , то

.

Составим таблицу координат узлов и значений функций тока в них. Таблица 5.1 позволяет определить энерговыделение на линиях разрыва скорости.

Таблица 5.1

№ узла	1	2	3	4	5
		0			0
	0	0	0
	0	0	0

Заметим, что не на всех сторонах треугольников имеет место разрыв касательной составляющей скорости. Так, на сторонах и .

Таким образом, энерговыделение имеет место лишь на линиях разрыва скорости и , а также на линии пластического контакта , если .

Построим функции тока в треугольниках разбиения.

Согласно зависимости (5.15) в треугольнике 1-2-5:

, , (5.16)

а в треугольнике 2-3-4

, .

Далее, в треугольнике 2-4-5 .

По формулам (5.13) определим составляющие скорости:

, (5.17)

(5.18)

По результатам вычислений составляющей скорости (5.16)-(5.17) строим годограф скоростей (рис. 5.5)

Нетрудно проверить, что годограф скоростей (рис. 5.5) удовлетворяет граничным условиям задачи и соответствует разрывному полю линий скольжения (рис. 5.4). Действительно, вектор скорости в треугольнике 2-4-5 направлен параллельно , т. е. выполняется условие непроницаемости на линии контакта с инструментом, а в условие несжимаемости удовлетворяется тождественно

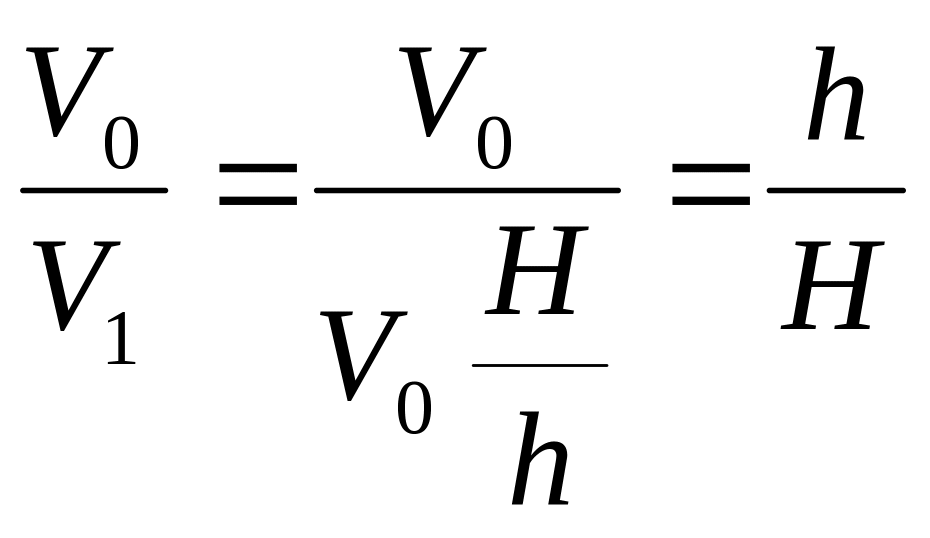
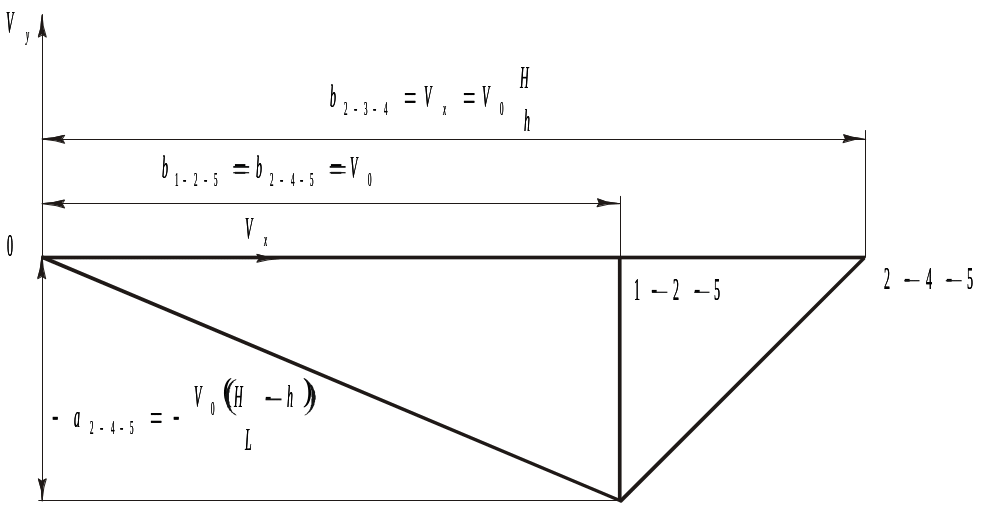
Рис. 5.5

По формуле (5.11) найдем энерговыделение на линиях разрыва скорости:

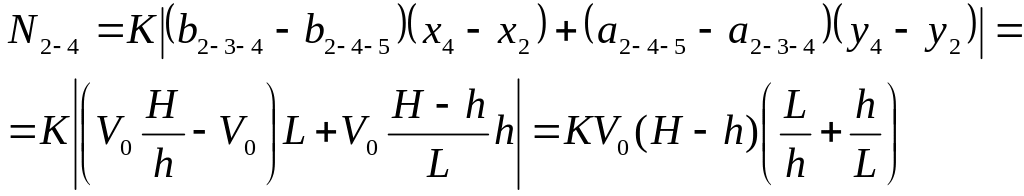(5.19)

На линии

. (5.20)

На линиях 1-5 и 2-4 разрыв скорости отсутствует, следовательно

. (5.21)

Найдем энерговыделение на линии контакта заготовки с инструментом. Для этого введем фиктивный треугольник 5-4-6 (рис. 5.4).

Так как матрица неподвижна, то

, .

Теперь применим формулу (5.9):

(5.22)

Полное энерговыделение процесса равно

. (5.23)

Удельное усилие редуцирования определим по формуле (5.7):

. (5.24)

При волочении деформирование осуществляется протягиванием заготовки через фильеру. В этом случае

, (5.25)

т. е. удельное усилие волочения при тех же параметрах деформирования в больше, чем при редуцировании.

Формулу (5.24) можно уточнить. Если ввести варьируемые параметры, как это делается в методе верхней оценки. Так можно варьировать координатой вершины 2 (рис. 5.4) или увеличить число элементов разбиения, как это показано, например, на рис. 5.6.

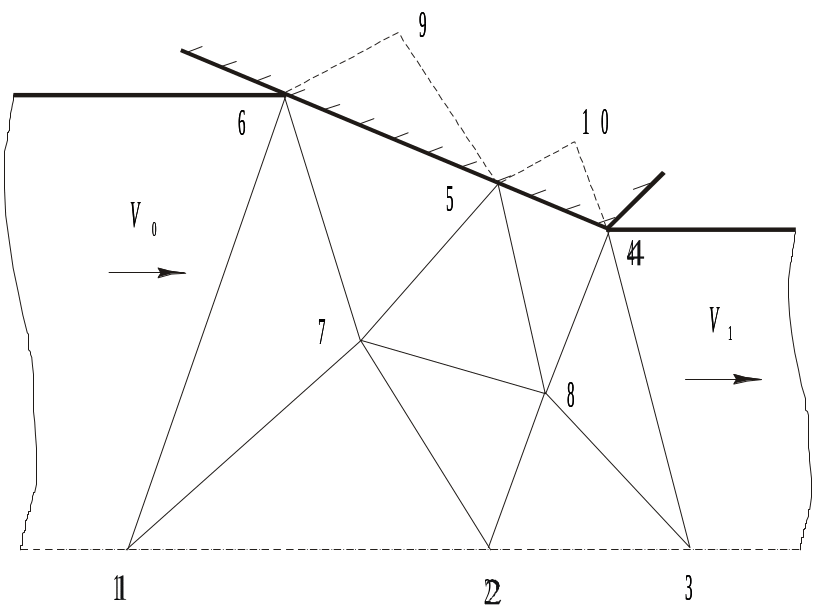
Рис. 5.6

Здесь варьируемыми параметрами могут быть координаты , а также значение функции тока в узле 8 – . Таким образом, задача сводится к поиску минимума функции энерговыделения от шести переменных. Такую задачу лучше решать с помощью ЭВМ.

Пример расчета

Определить полное удельное усилие редуцирования полосы в матрице с углом ската , если начальная высота полосы , конечная высота полосы , ширина полосы .

Предел текучести материала Коэффициент трения .

Определим длину проекции контактной линии на ось (рис. 5.4):

,

.

Из формулы (5.24) имеем

Полное усилие процесса

т кН.

Заметим, что удельное усилие осесимметричного процесса можно приближенно определить по формуле, предложенной А. Д. Томленовым: