4.4. Определение удельного усилия при прямом прессовании

Рассмотрим установившийся процесс плоской деформации неупрочняющегося материала. Сначала допустим, что трение на поверхности контакта между материалом и инструментом отсутствует.

Принятое кинематически возможное поле показано на рис.2 а. Для построения скоростей из точки 0 (рис.2. б) откладываем вектор , а затем из точки 0 и 1 проводим прямые 02 и 12, параллельные линиям скольжения 02 и 12, пересечение которых определяем положением точки 2. Материал в области 3 движется вертикально. Проводя прямую 23, параллельную линии скольжения 23 до пересечения с вертикалью 03 , получим положение точки 3. Вектор 03 будет соответствовать скорости движения выдавливания материала.

Верхняя оценка удельного усилия будет определяться с учетом симметрии по формуле

. (4.59)

где - длина участка скольжения ;

- скорости скольжения на соответствующих участках ;

- скорость движения инструмента.

Выражая все величины через размеры а, в и h и, принимая, получим:

, (4.60)

где в и а - соответствуют половине ширины сечения до и после прессования ;

h - высота принятой зоны пластической деформации.

Исследуя функцию на экстремум по переменной h, получим, что усилие будет минимальным при условии

(4.61)

и составит

^. (4.62)

Заменяя размер a, b через обжатие , окончательно получим

; (4.63)

Если на стенках контейнера имеются силы трения, получим

, (4.64)

которое будет минимальным при условии

(4.65)

и равно

(4.66)

При решении осесимметричных задач удобнее использовать разложение скорости относительного скольжения на компоненты по двум взаимно перпендикулярным направлениям , одно из которых совпадает с осью симметрии. Подобное поле скоростей (рис.3) можно использовать и при решении плоской задачи. Тогда формулу (4.60) можно представить в виде

(4.67)

где скорости U и V (рис.4) определяются из условия сплошности среды:

для плоской задачи

(4.68)

Для осесимметричного прессования

(4.69)

Удельное усилие в последнем случае будет определятся по формуле

(4.70)

которая после исследования на экстремум позволяет определить глубину зоны пластической деформации

(4.71)

и минимальную верхнюю оценку удельного усилия

(4.72)

4.5. Определение величины сопротивления деформированию с учетом деформационного и скоростного упрочнения

Рассматривается задача по осадке цилиндра. При расчете используется аппроксимация кривой упрочнения в виде

Д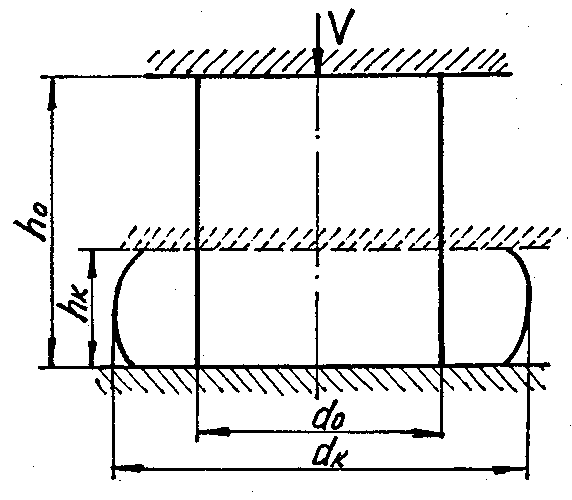 ано:

Рис. 4.7