
- •I. Механика
- •Система отсчета. Радиус-вектор, перемещение, путь, скорость.
- •Ускорение материальной точки (нормальное и тангенциальное). Движение точки по окружности.
- •Равноускоренное прямолинейное движение материальной точки.
- •Инерциальные системы отсчета. Первый закон Ньютона. Принцип относительности Галилея. Закон сложения скоростей.
- •Сила. Второй закон Ньютона. Масса. Третий закон Ньютона.
- •Импульс. Закон сохранения импульса.
- •Работа и мощность. Теорема о кинетической энергии.
- •Потенциальные и непотенциальные силы. Механическая энергия. Закон сохранения и изменения механической энергии.
- •Векторы угловой скорости и углового ускорения. Связь между линейными и угловыми величинами.
- •Момент силы, момент импульса, закон изменения момента импульса. Уравнение моментов.
- •Основной закон динамики вращательного движения твердого тела.
- •Момент инерции. Кинетическая энергия вращения.
- •Гармонические колебания. Смещение, скорость, ускорение при гармонических колебаниях. Дифференциальное уравнение гармонических колебаний.
- •Гармонические колебания груза на пружине. Период колебаний.
- •Превращения энергии при гармонических колебаниях груза на пружине.
- •Затухающие колебания. Логарифмический декремент затухания.
- •Вынужденные колебания. Резонанс.
- •Физический и математический маятник. Период колебаний маятника.
- •Моль вещества, молярная масса. Число Авогадро. Законы идеальных газов (изопроцессы). Уравнение Менделеева-Клапейрона.
- •Распределение Максвелла. Средняя квадратичная скорость молекул.
- •Основное уравнение молекулярно-кинетической теории идеального газа.
- •Внутренняя энергия идеального газа. Закон равномерного распределения энергии по степеням свободы.
- •Работа в термодинамике. Выражения для работы при изопроцессах идеального газа.
- •Первое начало термодинамики. Количество теплоты. Теплоемкость идеального газа. Уравнение Майера.
- •Адиабатический процесс. Уравнение Пуассона.
- •Принцип действия теплового двигателя и его к.П.Д.
- •Цикл Карно и его к.П.Д.
- •Обратимые и необратимые процессы. Энтропия идеального газа. Статистический смысл энтропии.
Гармонические колебания. Смещение, скорость, ускорение при гармонических колебаниях. Дифференциальное уравнение гармонических колебаний.
Простейшим частным случаем периодических колебаний являются гармонические, т. е. такие, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Этот вид колебаний особенно важен по следующим причинам:
1) колебания в природе и технике часто имеют характер, близкий к гармоническому;
2) периодические колебания иной формы (с иной зависимостью от времени) могут быть представлены как наложение нескольких гармонических колебаний.
Примером таких колебаний может служить
изменение проекции радиус-вектора А,
вращающегося с постоянной угловой
скоростью 0 (рис.
7.1). При этом координата x конца
радиус-вектора изменяется по гармоническому
закону: xAcos(0t0),
или xAsin(0t0),
где
А, 0, 0
– постоянные величины. Координату
x в данный момент времени называют
смещением.

Максимальное значение A колеблющейся величины называется амплитудой. Выражение 0t 0 называется фазой колебания и определяет значение величины x в данный момент времени. Величина 0 определяет значение фазы в момент времени t 0 и называется начальной фазой. Смысл фазы в том, что она отражает состояние колебательного процесса. Зная фазу , можно по уравнению x Acos найти значение колеблющейся величины, а также характер ее изменения. Например, если фаза / 3, то это означает, что x A/2, и в данный момент величина x убывает. Таким образом, значения колеблющейся величины и скорости ее изменения вполне определяют состояние колебательного процесса.
Последовательно продифференцировав уравнение гармонических колебаний по времени, получим выражения скорости v и ускорения a материальной точки вдоль оси X:

где v0 А0 и а0 А02. Из приведенных выражений видно, что скорость частицы v также
изменяется по гармоническому закону, причем амплитуда скорости равна А0. Сравнивая выражение скорости с выражением смещения x, находим,
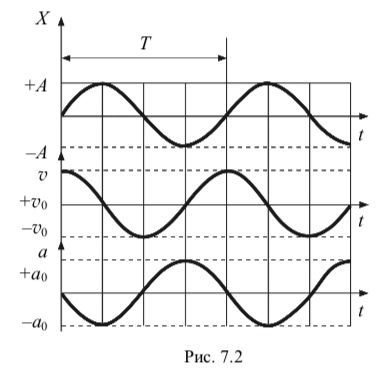
что скорость опережает координату x в данный момент времени по фазе на / 2 (рис. 7.2).
Выражение для a также позволяет сделать вывод, что ускорение из-
меняется по гармоническому закону с амплитудой А02. Отсюда же следует, что ускорение и смещение находятся в противофазе. Это означает, что, когда смещение достигает наибольшего положительного значения, ускорение достигает наибольшего отрицательного значения, и наоборот (рис. 7.2).
Из сказанного следует, что если материальная точка совершает гармонические колебания, то справедливо уравнение а 02 x.
Математически можно показать, что эта
связь ускорения и смещения является
необходимым и достаточным условием
того, чтобы тело совершало гармонические
колебания около положения равновесия.
Следовательно, если при анализе
поставленной задачи будет найдено, что
а Cx,
где С – положительная константа,
то тело будет совершать гармонические
колебания около положения равновесия
с циклической частотой
 .
.
 По
второму закону Ньютона mаXFрез.X,
где F – проекция результирующей всех
сил, действующих на тело, на ось X,
вдоль которой совершаются колебания.
В результате получаем Fрез.X
m2x.
По
второму закону Ньютона mаXFрез.X,
где F – проекция результирующей всех
сил, действующих на тело, на ось X,
вдоль которой совершаются колебания.
В результате получаем Fрез.X
m2x.
Из этого уравнения следует, что равнодействующая всех сил, действующих на тело, совершающее гармонические колебания, прямо пропорциональна смещению и направлена в сторону, противоположную ему. Силы, пропорциональные смещению и направленные в противоположную сторону, т. е. удовлетворяющие условию FX kx, но имеющие иную природу, чем упругие, называются квазиупругими. Гармонические колебания совершаются под действием упругих и квазиупругих сил.
Дифференциальное уравнение
![]()
