8. Потенциальные и непотенциальные силы. Механическая энергия. Закон сохранения и изменения механической энергии.

По характеру совершения работы различают потенциальные и непотенциальные силы. Силы, работа которых не зависит от вида траектории, по которой перемещается тело, а определяется только начальным и конечным его положением, называются потенциальными. В механике к таким силам относят силы тяготения и силы упругости. Силы, работа которых зависит от вида траектории, называются непотенциальными. К таким силам относятся силы трения.

Механической энергией W_мех называется скалярная физическая величина, которая характеризует движение и взаимодействие тел и зависит от их скоростей и взаимного расположения. Количественно механическая энергия определяется максимальной работой, которая может быть совершена вследствие изменения скоростей тел и их взаимодействия, обусловленного взаимным их расположением или частей одного и того же тела относительно друг друга.

Механическая энергия является суммой кинетической и потенциальной энергии.

В общем случае на тела механической системы могут действовать как потенциальные, так и непотенциальные силы, и полная работа, совершаемая при переходе системы из одного состояния в другое, будет равна AA_пA_нп.

В соответствии с теоремой о кинетической энергии эта работа равна AW_кW_к2 W_к1.

Работа же потенциальных сил определяется убылью потенциальной энергии: A W_п W_п1 W_п2.

Таким образом,

AW_п  A_нп,

или

W_к W_п  A_нп.

С учетом того, что W_к  W_{к 2}  W_к1, получаем W_к2 W_к1 W_п1 W_п2 А_нп. Полученное выражение можно записать в виде

(W_к2 W_п2 )(W_к1 W_п1 )А_нп.

Выражения в скобках представляют собой механическую энергию системы тел в начальном W₁ и конечном W₂ состоянии. Таким образом, W₂ W₁  A_нп, т. е. изменение механической энергии системы тел определяется работой непотенциальных сил.

Если в системе тел действуют только потенциальные силы, то A_нп  0, и в этом случае W₂  W₁. Это равенство выражает закон сохранения механической энергии: полная механическая энергия системы тел, в которой действуют потенциальные силы, остается постоянной.

9. Векторы угловой скорости и углового ускорения. Связь между линейными и угловыми величинами.

Движение по окружности является простейшим примером криволинейного движения. Положение материальной точки при этом виде движения (рис. 1.18) задается в любой момент времени t либо длиной дуги s, равной пройденному за промежуток времени t пути, либо углом поворота φ радиус-вектора r, определяющего положение этой точки на траектории относительно центра окружности.

Движение по окружности называется равномерным, если за любые равные промежутки времени точка проходит одинаковый путь.

Линейная скорость v материальной точки, движущейся по окружности, равна отношению пройденного пути (длине дуги) s к промежутку времени t, за который этот путь пройден: .

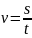Угловой скоростью движения точки по окружности называется отношение угла поворота φ радиус-вектора r точки за промежуток времени t к длительности этого промежутка: .

Угол поворота φ (угловой путь) измеряют в радианах (рад), а угловую скорость  в радианах в секунду (рад/с). Угол поворота можно измерять также числом оборотов N, совершенных точкой за промежуток времени t.

Связь между этими величинами устанавливается соотношением 2N.

С учетом этого выражение угловой скорости принимает следующий вид:

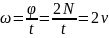, где величина = называется частотой вращения, равно1 числу полных оборотов, совершаемых точкой за единицу времени. Величина, равная промежутку времени, в течение которого точка совершает один полный оборот, называется периодом вращения T: T= .

Период вращения T можно выразить через линейную v и угловую 

скорость следующим образом: T= , где R – радиус окружности, по которой движется материальная точка. Пройденный материальной точкой к моменту времени t путь s и угол поворота φ определяются соотношениями svt, t.

При этом путь s и угол поворота φ связаны между собой равенством sR,

из которого следует связь между линейной и угловой скоростью: vR.

Так как при равномерном движении по окружности вектор линейной скорости v точки изменяется по направлению, оставаясь постоянным по модулю, точка движется с ускорением a_n, модуль которого определяется следующими выражениями:

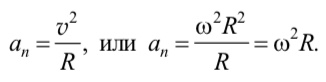
Вектор ускорения a_n направлен к центру окружности, и поэтому ускорение точки, равномерно движущейся по окружности, называют центростремительным, или нормальным.