14. Гармонические колебания груза на пружине. Период колебаний.

Рассмотрим в качестве примера систему, состоящую из шарика массой m, подвешенного на пружине, массой которой можно пренебречь по сравнению с m. В положении равновесия сила тяжести уравновешивается упругой силой (рис. 7.3) mg  kl₀, гдеl₀ –удлинение пружины.

Будем характеризовать смещение шарика из положения равновесия координатой x, причем ось X направим по вертикали вниз, а точку O (начало отсчета) совместим с положением его равновесия.

Если сместить шарик в положение, характеризуемое координатой x, то удлинение пружины станет равным l₀  x, и проекция результирующей силы на ось X примет значение Fmgk(l₀ x).

Учитывая условие mg  kl₀ , получаем F  kx, т. е. результирующая силы тяжести и упругой силы имеет характер квазиупругой силы.

С учетом этого уравнение второго закона Ньютона для шарика примет вид

где означает вторую производную смещения по времени; ₀²  k / m – собственная частота колебаний. Таким образом, в отсутствие сил трения движение под действием квазиупругой силы описывается дифференциальным уравнением

Общее решение этого уравнения имеет вид

x  Acos(₀ t  ₀ ).

Периодом колебания Т называется наименьший промежуток времени, по истечении которого значения всех величин, характеризующих колебательное движение, повторяются. За это время совершается одно полное колебание.

15. Превращения энергии при гармонических колебаниях груза на пружине.

Если колебания тела происходят по закону x  а cos(₀t  ₀ ), то кинетическая энергия этого тела

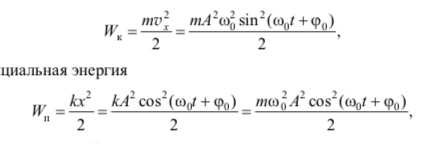
а потенциальная энергия

при этом за нулевой уровень отсчета принимается положение равновесия x = 0.

Сложив кинетическую и потенциальную энергию с учетом соотношения m₀²  k, получим формулу полной энергии гармонического колебания

Из нее следует, что полная энергия гармонического колебания является величиной постоянной.

Действительно, поскольку квазиупругая сила является консервативной, то в отсутствие сил трения полная механическая энергия гармонического колебания должна оставаться постоянной. В процессе колебаний происходит превращение кинетической энергии в потенциальную и обратно, причем в моменты наибольшего отклонения от положения равновесия полная энергия E состоит только из потенциальной, а при прохождении системы через положение равновесия она состоит только из кинетической энергии.

Из приведенных формул следует, что

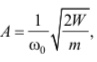
т. е. амплитуда гармонических колебаний определяется энергией, сообщенной системе.

Используя тригонометрическую форму записи формул, можно показать, что W_п и W_к изменяются с частотой 2₀, т. е. с частотой, в два раза превышающей частоту гармонического колебания.

16. Затухающие колебания. Логарифмический декремент затухания.

Во всех реальных случаях помимо квазиупругой силы на тело действует сила сопротивления, которая обычно считается пропорциональной скорости: Fсопр.rv, где r – коэффициент сопротивления. Уравнение второго закона Ньютона при наличии силы сопротивления имеет вид

или

где ₀ – частота собственных колебаний;   r / (2m) – коэффициент затухания.

Решение этого дифференциального уравнения при не слишком сильном затухании имеет вид

xА₀exp(t)cos(t₀), где

Отсюда видно, что амплитуда колебаний не является постоянной величиной, а уменьшается со временем по экспоненциальному закону: А(t)  А₀exp(t), где A₀ – начальная амплитуда колебаний. Следовательно, колебания при наличии силы сопротивления не являются гармоническими. Такие колебания называют затухающими.

Постоянная величина ω называется круговой частотой затухающих колебаний. Величина ₀ является круговой частотой колебаний в отсутствие сопротивления среды (0) и называется собственной частотой колебаний.

Вследствие работы силы сопротивления механическая энергия в процессе колебаний непрерывно уменьшается, переходя во внутреннюю энергию. Соответственно амплитуда колебаний уменьшается, и колебания постепенно затухают (рис. 7.5). Однако смещение x принимает нулевые значения через равные промежутки времени

Поэтому время T, определяемое этой формулой, и частота рассматриваются как условные период и частота затухающих колебаний. Быстроту убывания амплитуды характеризуют величиной, называемой логарифмическим декрементом затухания

где А(t) и А(t  T ) – значения амплитуд, соответствующих моментам времени, отличающимся на период. Воспользовавшись уравнением для A(t), получим

откуда следует   T.