
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf
отрима¹мо також цiкавий резульòàò
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
X |
|
|
|
1 |
|
|
|
|
|
|
|
π2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Це сво¹ю чергою да¹ |
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
= |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
=1,3,5,... |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
∞ |
1 |
|
|
|
X |
|
|
|
|
|
|
1 |
|
|
|
|
|
X |
|
|
|
|
1 |
|
|
|
|
|
π2 |
|
|
|
|
1 |
|
|
∞ |
1 |
|
|||||||||||||||
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|||||||||
çâiäêè |
|
|
n2 |
= |
|
|
|
|
|
|
|
|
n2 |
+ |
n=2,4,... |
n2 |
= |
|
8 |
|
+ |
|
|
4 |
|
n=1 |
n2 |
, |
|||||||||||||||||||||||||||
|
n=1 |
|
|
|
|
n=1,3,5,... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
1 |
|
|
|
|
|
π2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Приклад. Хвильова ункцiячаñòèíêè= |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
n2 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
За означенням, хвильова |
|
|
|
|
|
|
|
|
|
в iмпульсномуψn (x)зображеннiв iмпульсному зображеннi. |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Z a e−ipx/~ |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Z a |
|
−ipx/~ |
|
|
|
|
|
π |
o |
|||||||||||||||||||||
|
C(p) |
|
= |
|
|
|
√ |
|
|
|
|
|
ψn(x) dx = |
√ |
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
sin |
|
a |
nx dx |
||||||||||||||||||||
|
|
|
|
|
|
~ |
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
2π |
|
|
|
|
|
|
|
pa |
|
|
|
π |
|
|
|
πa n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
озподiл за |
|
|
|
|
|
√ |
|
|
|
|
sin |
|
~ |
+ |
2 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
pa |
|
|
|
π |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
iмпульсами ~3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
(πn~)2 − (pa)2 exp |
|
2~ + 2 (n − 1) . |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
= |
|
|
2n |
πa |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
4πa~3n2 |
|
|
|
|
|
|
|
|
2 pa |
|
π |
|
|
|
|
|
|
|
||||||||||||||||||||
Очевидно повинна|C(p)| = |
(π2n2~2 |
|
− p2a2)2 |
sin |
|
|
|
|
+ |
|
n . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
2~ |
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
виконуватись умова |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z∞ |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перевiрмо ¨¨. Зробимо замiну|Cзмiнно¨(p)| dpiнте= 1.рування |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
i знайдемо |
|
|
|
|
|
|
|
|
|
|
|
|
|
x = pa/2~ + πn/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Z∞ |
|
|
|
|
2 |
|
|
|
|
|
π |
|
2 |
Z∞ |
|
|
|
|
sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
182 |
|C(p)| |
|
dp |
= |
|
|
|
n |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
−∞ |
|
x2(πn − x)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

|
|
|
|
π 2 |
Z∞ sin2 x |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||
|
|
= |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
dx |
||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
(äèâ |
|
|
2 |
|||||||||||
Мштейн.:Наука,И.С.1971,ыжикнасторИ.αÌ.=463). Таблицыπn.iIíòå |
|
|
(πn − x) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
2 |
|
|
0 |
|
|
x |
|
|
|
|
|
|
|
|
|
πn + x) |
|
|||||||||||||||||
|
|
|
|
π 2 |
|
|
|
d |
Z∞ sin2 x |
|
1 |
|
|
|
|
1 |
|
||||||||||||||||||||
|
Z∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
= |
|
2 n −dα |
0 Z∞ x2 |
sin |
2α |
− x |
+ |
α + x dx |
|||||||||||||||||||||||||||
тимчасове позначення = |
|
2 |
|
− |
|
d |
α 0 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
dx, |
|
|
|
|
|
||||||||||
πn |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
dα |
|
x2(α2 − x2) |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
теперинтегралов,¹абличнимсумм, рядов.наприклад,произведенийрад-. |
||||||||||||||||||||||||||||||
|
|C(p)| |
2 |
|
|
|
2 |
− |
|
d |
|
π |
|
|
|
2 − |
|
sin 2α |
|
|
|
|||||||||||||||||
|
|
dp = πn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
dα |
4α |
|
|
|
|
α |
|
|
|
|
|
|||||||||||||||||||||||
|
−∞ |
πn |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2α |
|
|
|
|
|
|
|
|
|
|
|
||||||||
îñêiëüêè |
= |
|
|
|
|
1 + cos 2α − |
|
|
|
|
|
|
|
= 1, |
|
|
|
|
|
||||||||||||||||||
2 |
|
α2 |
|
α |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
систему,УкласичнiйŸα21=óíêöiÿ.πn.армонiчниймеханiцiамiльтонгосциляторàрмонiчнимяко¨. Хвильовийосциляторомпiдхiдназивають
|
|
|
|
p2 |
mω2 |
|
|
|
||
озв'язки класичних рiвняньH = |
|
ðóõó+ äîáðåx2 |
.âiäîìi: |
|||||||
|
|
|
|
2m |
2 |
|
|
|
||
|
|
x = x0 sin(ωt + δ), |
|
|
|
|||||
ω iÿ |
|
|
x0 |
|
|
|
|
δ |
|
|
òóò |
|
p = mωx0 cos(ωt + δ), |
|
|
||||||
Åíåð |
частотнабува¹коливань, |
|
|
àìïëiòóäà, |
|
початкова аза. |
||||
|
E |
неперервний ряд значень: |
|
|||||||
|
|
|
|
|
|
mω2 |
|
|
|
|
|
|
E = |
|
x02. |
|
|
183 |
|||
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|

Ó |
|
механiцi iмпóëüñ ò |
к ординату замiню¹мо на опе- |
||||||||||||||||||
раториквантовiй. Т дi гамiльтонiан гармонiчíîãî |
осцилятора |
||||||||||||||||||||
|
|
|
|
|
|
ˆ |
|
|
|
pˆ2 |
mω2 |
2 |
|
|
|
|
|
|
|||
Завдання поляга¹ в знаходженнiH = +ðîçâ'ÿçêóxˆ . рiвняння Шредин ера |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2m |
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
власнi ункцi¨акийвласт |
||||||
нiIншимизначенлянемословами,оператнамбражнеобхiдноHψ =вiдшукатиEψ. |
|||||||||||||||||||||
динатн |
|
|
|
|
ˆ |
|
|
|
(квантоваξ = x/l0 |
|
l0 = p~/mω |
||||||||||
гляд:У коорозг |
|
муспочаткузH.åííiïiäõðiдвняннянаосновiШрединхвильово¨ера ма¹ мехтанiки-. |
|||||||||||||||||||
~2 d2 |
ψ(x) |
|
mω2 |
2 |
|
|
|
|
|
|
|
|
|
|
−∞ < x < ∞. |
||||||
ìî çнерозìiðåíó |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
величинуx ψ(x) = Eψ x), |
|
||||||||||||||||||||
Уведе−2m dx2 |
|
+ |
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
церактернийрiвняння:масштаб довжини |
|
|
|
|
àìïëiòóäà), äå |
. Знерозмiримоха- |
|||||||||||||||
|
|
|
|
|
d2 |
ψ(ξ) |
|
|
|
|
|
|
2E |
|
|
|
|
|
|||
енерЗ iзичнихi¨ при |
|
|
|
íü, áåðó÷è2до уваги |
|
зростання потенцiально¨ |
|||||||||||||||
|
|
|
|
||||||||||||||||||
|
мiркува− |
dξ2 |
|
+ ξ ψ(ξ) = ~ω |
ψ(ξ). |
|
|
|
|||||||||||||
|
|
частинавиплива¹,рiвняннящопряму¹ |
|
ля швидше,.Уцьомунiж |
|||||||||||||||||
лiва:випадку праваx → ±∞ |
|
|
|
|
|
|
|
ψ → 0 |
придонуξ → ±∞ |
||||||||||||
|
|
|
|
|
|
d2ψ(ξ) |
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
наченнÿõ |
ψ(ξ) = 0. |
|
|
|
|
||||||||||
Îòæå, ïðè |
велик чниз−õ |
dξ2 |
|
|
+ ξ |
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
ξ |
ðîçâ'ÿçîê |
рiвняння ψ(ξ) |
|||||||
exp(льова±ξ /óíêöiÿ2). Ç içöié |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
вiдкида¹мо, i хви- |
|||||||
|
|
|
è границiмiркувань, знак + |
||||||||||||||||||
що хвильову ункцiю можнаψзобразити(ξ) exp(−òàê:ξ /2). Звiдси виплива¹, причому невiдома ункцiяψ(ξ) = CH(ξ)e−ξ2/2,
тати швидше, нiж |
H(ξ) на безмежностi е повинна зрос- |
184 |
exp(ξ2/2), C стала нормуваííÿ. |
Пiдстановка цього виразу в рiâíÿння Шредин ера да¹
Запишемо |
|
H′′(ξ) − 2ξH′(ξ) + ~ω − 1 H(ξ) = 0. |
|
|
|
||||||||||||||||||||
|
|
|
|
íåâiäîìó óíêöiþ |
|
|
2E |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
H(ξ) у виглядi ряду |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
k |
|
|
|
|
|
|
||||
i пiдставимо його в рiвняння. Ма¹мо |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
H(ξ) = |
|
|
ak ξ |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k≥0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
k |
|
2 |
|
X |
|
|
|
k |
|
|
|
2E |
|
|
X |
|
k |
|
|||
Ó |
k 2 ak k(k − 1)ξ |
− |
|
− 2 k 0 ak kξ |
|
+ |
~ω |
|
− 1 k 0 akξ |
|
= 0. |
||||||||||||||
|
першо у доданку поклада¹мо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
≥ |
|
|
|
|
|
|
|
≥ |
|
|
|
|
|
|
|
|
|
|
|
|
≥ |
|
|
|
познача¹ìо через |
|
|
|
|
|
|
|
k − 2 = k′, à ïîòiì k′ |
знову пере- |
||||||||||||||||
|
X |
|
k: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2E |
|
|
|
k |
|
|
||||
рiвнянняно,Длящобтогокщобдляжнийневiдомихсумачленстепеневогорядукоедорiвнювавiцi¹нтiвяду дорнулевi.iâíювалаЦе нулевi,да¹рекурентненеобхiд- |
|||||||||||||||||||||||||
|
k |
≥ |
0 (k + 2)(k + 1)ak+2 |
− |
2kak |
+ |
~ω |
− 1 ak ξ |
|
= 0. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ak: |
|
|
|
|
|
|
||||
|
|
|
|
|
значеннях |
|
|
2k + 1 |
|
2E/~ω |
|
|
|
|
|
||||||||||
При великих |
= ak |
|
|
|
|
− |
|
|
|
|
. |
|
|
|
|
||||||||||
ak+2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(k + 2)(k + 1) |
|
|
|
|
||||||||||
бачимо, що для кое iцi¹нтiвk знахпарнимиодимо, значкамищоa |
= 2a /k. Çâiäñè |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k+2 |
|
k |
|
|
|
ÿä äëÿ |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
a2k 1/k!, íàø |
|||||
не буде задовH(ξ) да¹льнятиH(ξ)граничнихexp(ξ ). умовУрезультатi хвильова ункцiя |
|||||||||||||||||||||||||
забезп чення îбрива¹мо |
яд, покладаючиψ → 0, ξ → ±∞. Для ¨х |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an+2 = 0, àëå an 6= 0: |
|||||||
|
Це рiвняння визнача¹2n +ðiâíi1 −åíåð2E/~i¨ω = 0. |
|
|
|
|
|
|
||||||||||||||||||
лятора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E = En гармонiчного осци- |
||||||||||
|
|
|
|
En = ~ω(n + 1/2), |
|
|
|
n = 0, |
1, 2, . . . |
|
|
185 |
|||||||||||||
|
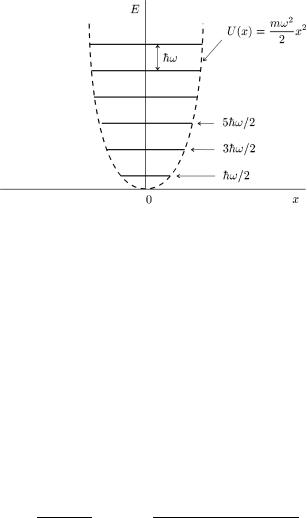
ис. 19. iвнi енер i¨ лiнiйного гармонiчного осцилятора. |
|
|
|||||||||||||||||||
вони, як бачимо, ¹ еквiдистантними (див. рис. 19). При цьому |
||||||||||||||||||||||
êîå iöi¹íòè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
à óíêöiÿ |
|
|
|
ak+2 |
= ak |
|
|
2(k − n) |
, |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
(k + 2)(k + 1) |
|
|
|
|
|
|
|
|||||
|
H(ξ) = Hn(ξ): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
за полiномвжедавньоюЕрмiтдомовленiстю,.Оскiлькисталавибира¹монормуванняk кое iцi¹нтщене привизначена, |
||||||||||||||||||||||
|
|
|
|
|
|
|
Hn(ξ) = |
|
ak ξ |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
k=0 |
|
|
|
|
|
|
|
|
|
|
íèì |
2n, решта знах димо з рекурентних спiввiдношень: |
ξn ðiâ- |
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||
HÄåêiëüêà(ξ) = (2першихξ) |
|
− |
|
(2ξ) |
− |
|
+ |
|
− |
|
− |
|
− |
|
(2ξ) |
|
− |
+. . . |
||||
|
n |
− |
n(n |
|
1) |
|
n |
2 |
|
n(n |
|
1)(n |
|
2)(n |
|
3) |
|
n |
4 |
|
||
n |
|
|
полiномiв мають |
вигляд: |
|
|
|
|
|
|
|
|
||||||||||
|
|
1! |
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
||||
|
H0(ξ) = 1, |
|
|
|
|
H3(ξ) = 8ξ3 − 12ξ, |
|
|
|
|
|
|
|
|||||||||
|
H1(ξ) = 2ξ, |
|
|
|
|
H4(ξ) = 16ξ4 − 48ξ2 + 12, |
|
|
|
|
|
|||||||||||
186 |
H2(ξ) = 4ξ2 − 2, |
|
|
H5(ξ) = 32ξ5 − 160ξ3 + 120ξ. |
|
|
|
|||||||||||||||
Виявля¹ться, що полiноми Ерìiòа можна записати в дуже |
||||||||||||||||
зручнiй ормi: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ2 |
d |
|
n |
ξ2 |
|
|
|
|
||
|
|
|
Hn(ξ) = e |
|
e− |
. |
|
|
|
|||||||
|
|
|
|
−dξ |
|
|
|
|
|
|||||||
нянняСправдi,дляневажкоункцi¨переконатись, що цей вираз задовольня¹ рiв- |
||||||||||||||||
можна |
зобразити |
|
H(ξ) |
ÿêùî åíåð iÿ |
|
E = En. Ïîëiíîì Åðìiòà |
||||||||||
|
|
òàê: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ2 |
d |
|
n |
|
ξ2 |
ξ2/2 |
|
|
d |
n |
ξ2/2 |
|
|||
|
e− |
|
|
e− |
. |
|||||||||||
|
Hn(ξ) = e |
|
−dξ |
|
= e |
|
|
ξ − dξ |
|
|||||||
Отже, хвильовi |
óíêöi¨ ãармонiчного осцилятîðà |
|
|
|
||||||||||||
Ñòàëi |
|
|
ψn(x) = Cne−ξ2/2Hn(ξ). |
|
|
|
|
|||||||||
Cn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нормуваннявважа¹мо.Дляцьогодiйснимипiдраху¹мовеличинамиiнтералiзнаходимо ¨х з умови |
||||||||||||||||||
Z−∞ |
|
|
|
|
|
|
|
|
Z−∞ |
|
|
|
|
|
|
|
||
∞ ψn′(x)ψn(x)dx = r |
|
mω |
Cn′Cn |
|
|
∞ e−ξ2 Hn′(ξ)Hn(ξ)dξ |
|
|||||||||||
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Z−∞ |
|
|
|
|
|
||||
|
|
|
|
|
~ |
|
|
∞ |
|
|
d |
n |
ξ2 |
|
||||
|
|
|
|
|
|
|
|
|
|
e− |
dξ. |
|||||||
Ми використали |
явний= Cn′Cnr mω |
|
|
Hn′(ξ) |
Í−dξ |
|
|
|||||||||||
вигляд пîëiíîìà Åðìiòà. |
åõàé |
|
|
|
||||||||||||||
iíòå ðó¹ìî |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n′ < n i |
||
n разiв частинами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Z−∞ |
|
|
|
|
|
|
|
|
|
|
Z−∞ |
|
|
|
|
|
|
|
∞ |
ралом при |
|
~ |
|
∞ |
ξ2 |
dnHn′(ξ) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
e− |
|
dξ. |
|
|
||||||
Ïîõiäíà ïiäψn′iíòå(x)ψn(x)dx = Cn′Cnr mω |
|
|
dξn |
|
|
|
||||||||||||
частинамите рал аковiж дорiвню¹ нулевin.′ ßêùî< n дорiвню¹ нулевi,розкрива¹моотже, iн
íî ïîëiíîì |
|
n > n′, òî |
ÿâ |
|
|
|
- |
|
зновуункцi¨отриму¹мо, |
iнте ралякi-дорiвкратнеповинною¹iнтебутинулевiрування.Якщо.От187 |
|
же, хвиль |
Hn′(ξ) п ртогональними,водимо ак само n′ |
|
|

мального, тостепеняпохiднi полiномаiд iнте .раломЦей внесокдають дорiвню¹внесок лише вiд макси- |
|||||||||||||||||||||||||||||||||
n = n′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2nn!. З умови |
|||||||
нормування |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Z−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Z−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
∞ |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
2 |
|
|
~ |
|
|
|
|
|||||||
1знаходимо= ψn2 (x)dx = Cn2r |
|
|
|
2nn! |
|
|
|
e−ξ |
|
dξ = Cn2r |
|
2nn!√π |
|||||||||||||||||||||
mω |
|
|
|
mω |
|||||||||||||||||||||||||||||
Отже, остаточно |
Cn = π~ |
|
|
|
√2nn! . |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
mω |
1/4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
ψn(x) = |
mω |
|
1/4 |
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||
причому |
|
|
|
|
|
√ |
|
|
e−ξ |
/2Hn(ξ), |
|||||||||||||||||||||||
π~ |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
2nn! |
|||||||||||||||||||||||||||||
одСтаниВхвильоваос¹невироджовному |
Z−∞ ψn′ψn dx = δn′,n. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ункцстаненими,iя.колидорiвню¹к жному значенню енер i¨ вiдповiда¹ |
|||||||||||||||||||||||||||||||
менше зíачення, але не |
|
|
|
n = 0нулевi:,енер iя осцилятора ма¹ най- |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
E0 |
= |
|
~ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
невизначеностейтак звана енерункцiяайзенбернульвиха:неколиваньможе2 бути.Цеодночаснонаслiдок принципу |
|||||||||||||||||||||||||||||||||
2 |
i = 0 |
Приклади |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hx2i = 0 i |
|||
hp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Хвильова(див. |
|
основногод Ÿ7). стану |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
ψ0(ξ) = |
mω |
1/4 |
|
|
|
ξ2/2 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
e− |
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
π~ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
дженогоЯк бачимо,станувона ¹ безвузловою. Хвильова ункцiя першого збу- |
|||||||||||||||||||||||||||||||||
ÿêà âiäïîâiä๠åíåðψ1i¨(ξ) = π~ |
|
|
|
e−ξ |
/2√2 ξ, |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
mω |
1/4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
188 |
|
E1 = 3~ω/2, ма¹ один вузол (рис. 20). |
|||||||||||||||||||||||||||||||
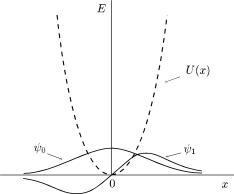
ис. 20. Хвильовi ункцi¨ лiнiйного гармонiчного осцилятора. |
|
Зроб мо уваження. Якщо розг |
задачу про рух час |
межноинкизв'язкиполiсокоюзапотенцiстiнкдорiвнюватильноюприенер i¹юлянутиmω2x2/попереднь2 ÿ x ≥ 0 êöi¨áåç
чц необхiдно врахувати ще |
|
- |
|
даткквантового,обрiзаногонашум ву:му хвильовi омуу ро в |
|||
цилятораглядi |
x = 0 |
|
|
x = 0заповиннепар овiим значенням нуле |
рмонiчногоÿþòü |
||
. Цю умовучисл задоволь, |
|||
Це будуть хвильумови, що ункцi¨ |
àê |
ãà n = 1, 3, 5, .îñ. .-. |
|
раторавласнiПочнемооператорiвŸзначення,22амiльтона.коордизармонiчнийтого,непородженняатинашо¨щоконкретизуючиxйзнову≥iмпульсузадачi,осцилятор0. запишемоперестзнищенняпредстрiвняння. Метоавнiихiднiавлення:спiвоператорiвна иразиiдношеннявласнiдляункцi¨опедля-
|
|
pˆ2 |
|
mω2 |
|
|
|
|
|
|
|
|
|
Hˆ = 2m + |
~ |
xˆ2, |
||||
|
2 |
|||||
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xˆpˆ pˆxˆ = i , |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
189 |
Hψˆ = Eψ. |
|
|
||||

кладамiльтонiанна простi¹ квадратмножíèêèчноюи . Дëÿормою,цього вiâåäåнапрмîшу¹тьсяоператорийого роз-
ˆb = √2 r |
|
xˆ + i √m~ω |
, |
|
~ |
||||
1 |
mω |
|
pˆ |
|
Вiзьмемо добутокˆb = √2 |
r |
|
|
|
|
|
|
|
|
xˆ − i |
√m~ω . |
|
||||||||||||||||||||||
|
|
|
~ |
|
|
|
||||||||||||||||||||||||||||
|
|
+ |
1 |
|
|
|
|
|
|
|
|
mω |
|
|
|
|
|
|
|
|
pˆ |
|
||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
pˆ2 |
|
||||
|
mω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
mω |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
тобто ˆb+ˆb = |
|
|
|
|
xˆ2 + r |
|
|
|
|
|
|
√ |
|
|
i(ˆxpˆ − pˆxˆ) + |
|
, |
|||||||||||||||||
2 |
~ |
|
|
~ |
|
|
|
m~ω |
||||||||||||||||||||||||||
|
|
|
|
|
|
m~ω |
||||||||||||||||||||||||||||
|
|
|
|
ˆ+ˆ |
|
mωxˆ2 |
|
|
|
|
pˆ2 |
|
1 |
|
|
|
|
|||||||||||||||||
Аналогiчно |
|
|
b b = |
|
|
|
|
|
|
+ |
|
|
− |
|
. |
|
||||||||||||||||||
|
|
|
|
2~ |
|
|
|
2m~ω |
2 |
|
||||||||||||||||||||||||
|
|
|
|
ˆˆ+ |
|
mωxˆ2 |
|
|
|
|
pˆ2 |
|
1 |
|
|
|
|
|||||||||||||||||
Так що переставнi спiввiдbb = ношенíÿ+ äëÿ öèõ+ îператорiв:. |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2~ |
|
|
|
|
|
|
|
|
|
2m~ω 2 |
|
||||||||||||||
Очевидно, що |
|
|
|
ˆˆ+ |
|
|
|
|
|
ˆ+ˆ |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
bb |
|
− b |
|
|
b = 1. |
. |
|
|
|
|
|
||||||||||||||||||||
Тому вихiдне рiвняння H = ~ω b |
|
|
|
b + 2 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
íàˆ власнi ˆзначенˆ |
íя та власнi ункцi¨ для |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
||
набира¹ вигляду: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подi¹мо злiва на це рiвнянняˆ ˆ îïåратором |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
~ω b |
+ |
b + 2 |
ψ = Eψ. |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
190 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ+: |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
||||
Використаймо тепер переставнiˆ ˆ ˆ |
|
спiввiдношенняˆ ˆ |
операторiв |
|
|||||||||||||||||
|
~ω b |
+ |
b |
+ |
b + |
1 |
b |
+ |
ψ = Eb |
+ |
ψ. |
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
ˆ+: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b, |
b |
|
~ω ˆb+ˆˆbb+ |
− b+ |
+ |
|
1 |
ˆb+ ψ = Ebˆ+ψ, |
|
||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
2 |
|
||||||||||||||||||
|
~ω ˆb+ˆb − 1 + |
1 |
ˆb+ψ = Ebˆ+ψ, |
|
|||||||||||||||||
|
|
|
|||||||||||||||||||
|
2 |
|
|||||||||||||||||||
значення,Мизновуале |
|
ˆ ˆ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
iльшеноюˆ я нанавласнiˆ ункцi¨ та власнi |
||||||||||||||||||
|
~ω |
b |
+ |
b + |
2 b |
+ |
ψ = (E + ~ω)b |
+ |
ψ. |
|
|||||||||||
|
прийшлизенерi¹ю,дозáðiâíÿí |
|
|
|
|
|
|
||||||||||||||
öi¹þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ω, з х ильовою унк- |
|||||
ˆ+ |
|
|
|
|
|
|
|
|
то хвильовiйb ψ. Отже,ункцi¨якщо хвильовiй ункцi¨ ψ âiäïîâiä๠åíåð iÿ E, |
||||||||
|
|
|
ˆ+ |
ψ åíåð iÿ E + ~ω: |
|
|||
|
|
|
ψ1 = b |
|
|
|||
цюжокПроводячидля |
|
|
ˆ+ˆ |
1 |
|
|
значень¹мотакийенер i¨:лан- |
|
|
аналогiчнiхвильових перетункцiйâореннявiдповiдниха далi, отрим |
|
||||||
|
~ω b b + |
2 |
ψ1 = (E + ~ω)ψ1. |
|
||||
ψ → E, |
|
|
|
|
|
|
|
|
|
ˆ+ |
ψ → E1 = E + ~ω, |
|
|||||
ψ1 = b |
|
|
||||||
|
ˆ+ |
ˆ+ 2 |
|
|
|
|
||
ψ2 = b |
|
ψ1 = (b ) ψ → E2 = E1 + ~ω = E + 2~ω, |
|
|||||
............................................................................... |
|
|||||||
|
теперˆ |
оператором |
|
|
|
|||
Ïîäi¹ìîψn = (b |
+ n |
|
= E + n~ω. |
|
||||
) ψ → En |
|
|||||||
|
|
|
|
|
ˆ |
|
||
|
|
|
|
|
b на наше вихiдне рiвняння |
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
~ωbˆ ˆb+ˆb + |
|
ψ = Ebψ,ˆ |
191 |
||
|
|
|
2 |
|||||
