
Богословская Г.П. Все лекции ТМО
.pdf
Дифференциальное уравнение теплопроводности
Для постоянных свойств среды ,cp, = const
Dt |
|
2 |
|
q |
|
= a |
t + |
v |
|
d |
|
c |
||
|
|
|
||
|
|
|
|
p |
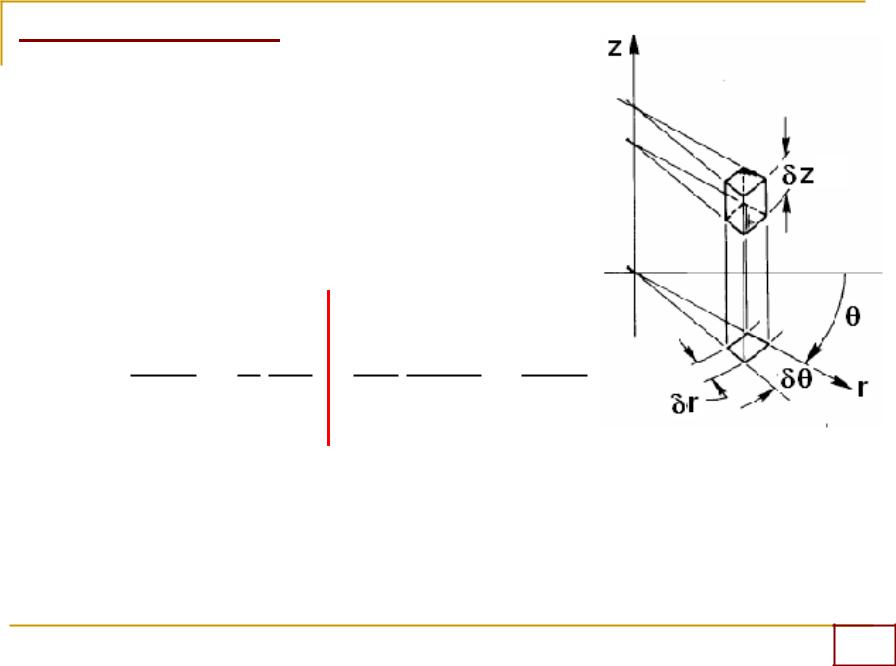
a = 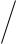 cp
cp
Для твердого тела (неподвижной среды), W=0
t |
|
2 |
|
q |
|
= a |
t + |
v |
|
|
|
c |
||
|
|
|
||
|
|
|
|
p |
При отсутствии внутренних источников тепла
t |
2 |
t |
|
= a |
|
|
|
Для стационарного случая
2t = 0
61

Запись Лапласиана
В декартовых координатах
|
2 |
|
|
2 |
t |
|
|
2 |
t |
|
|
2 |
t |
|||
|
t = |
|
|
+ |
|
|
+ |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
2 |
y |
2 |
z |
2 |
||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
62
Запись Лапласиана
В цилиндрических координатах
2t = |
|
1 |
|
|
t |
|
|
|
|
1 2t |
|
|
|
2t |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
r |
|
|
|
+ |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
r 2 q 2 |
|
z2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
r |
|
r |
|
|
r |
|
|
|
|
|
|
|
|
|
|||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
2 |
t |
|
1 t |
|
|
|
|
1 |
|
2 |
t |
|
|
2 |
t |
|||||||||||||
|
t |
= |
|
|
|
+ |
|
+ |
|
|
+ |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
r |
2 |
|
r r |
r |
2 |
q |
2 |
z |
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
63

Запись Лапласиана
В сферических координатах
2 |
|
|
|
|
1 |
2 |
( rt ) |
|
|
|
|
1 |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
t |
= |
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
r |
|
|
r |
2 |
|
|
|
|
|
r |
2 |
|
|
sin q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
sin q q |
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
2 |
q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
r |
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
2 |
t |
|
|
2 t |
|
|
1 |
|
|
|
2 |
t |
|
1 |
|
2 |
t |
|
1 |
|
t |
|||||||||||
|
|
|
t |
= |
|
|
|
+ |
+ |
|
|
|
|
+ |
|
+ |
ctgq |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
r |
2 |
|
r |
r |
2 |
sin |
2 |
q |
r |
2 |
q |
|
r |
2 |
q |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
||||||||||
64
Условия однозначности
Условия однозначности - замыкающие соотношения, которые выделяют конкретную задачу из общего класса задач
1. Геометрические условия |
форма и размеры среды |
2.Физические условия
3.Временные (начальные)
t = |
f (x, y, z, = 0) |
свойства среды |
,c |
p |
, |
|
|
значения температуры в начальный момент времени
4.Граничные условия
65

Граничные условия
Граничные условия требуют сопряжения температурных полей и тепловых потоков на границах тела с окружающей средой:
I рода – задание на границе распределения температуры:
t = |
f |
1 |
(x, y, z, ) |
|
|
|
в простейшем случае
t |
w |
= const |
|
|
II рода – задание на границе плотности теплового потока:
т.е. задание распределения
q = − |
t |
= f |
|
(x, y,z, ) |
|
n |
2 |
||||
|
|
|
|||
|
|
|
|
градиента температуры на границе
III рода – задание условий теплообмена
коэффициента теплообмена):
q = − nt = (tw −t f )
66

Граничные условия
Г.У. I рода |
Г.У. II рода |
Г.У. III рода |
67
СТАЦИОНАРНЫЕ
ПРОЦЕССЫ
ТЕПЛОПРОВОДНОСТИ
(продолжение)
68

Дифференциальное уравнение теплопроводности
c |
|
|
Dt |
= div( gradt)+ q |
|
|
|
||
p |
|
|
|
|
|||||
|
|
d |
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dt |
2 |
|
q |
|
|
|
|
|
|
|
t + |
|
v |
||
|
|
|
|
d |
= a |
c |
|
|
|
|
|
|
|
|
|
p |
|||
|
|
|
|
|
|
|
|
|
|
a = |
|
|
|
|
|
c |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
||
t |
|
(W grad t ) |
|
|
2 |
|
|
|
|||||
|
|
+ |
= |
a |
t |
+ |
|
v |
|||||
d |
|
c |
|
|
|||||||||
|
|
|
|
|
|
|
|
p |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
изменение |
изменение темп. поля, |
изменение темп. |
интенсивность |
||||||||||
температуры |
|||||||||||||
вызванное движением |
поля |
|
|
|
|||||||||
|
|
|
внутренних |
||||||||||
во времени |
среды |
в пространстве |
|||||||||||
источников тепла |
|||||||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
69

Распределение температуры в пластине
Найти:
стационарное распределение температуры в пластине
без внутреннего тепловыделения при Г.У. 1 рода
t d
0 +
0 |
0 |
|
2 |
|
q |
|
t + |
v |
||
(W grad t )= a |
c |
|
|
|
|
p |
|
стационарная |
неподвижная |
нет внутреннего |
|
задача |
|||
среда |
тепловыделения |
||
|
70
