Задача 2.13

При β-распаде ¹¹²Pd возникает β-активный нуклид ¹¹²Ag. Их периоды полураспада равны соответственно 21 и 3,2 ч. Найти отношение максимальной активности нуклида ¹¹²Ag к первоначальной активности препарата, если в начальный момент препарат содержал только нуклид ¹¹²Pd.

Решение. Будем обозначать индексом «1» величины, относящиеся к ¹¹²Pd, а индексом «2» величины, относящиеся к ¹¹²Ag. Тогда

; .

Искомое отношение

,

(2.13.1)

где N(t_m) – максимальное число атомов нуклида ¹¹²Ag, которое накапливается за время t_m (2.11.7). Используя (2.11.6), получим

.

(2.13.2)

Вычислим, используя (2.11.7),

10,2 ч,

а затем по формуле (2.13.2) рассчитаем

.

Задача 2.14

Радионуклид испытывает превращение по цепочке

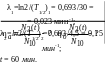( под стрелками указаны соответствующие периоды полураспада). Считая, что в начальный момент t = 0 препарат содержал только ¹¹⁸Cd, найти

а) какая часть ядер превратиться в стабильные ядра через 60 мин;

б) во сколько раз уменьшится активность препарата через 60 мин.

Решение а). Пусть N₁₀ – первоначальное количество ядер, а N₃(t) – количество образовавшихся ядер ¹¹⁸Sn за время t.

В свою очередь, количество образовавшихся ядер ¹¹⁸Sn за время t равно числу распавшихся ядер ¹¹⁸In за этот же промежуток времени:

,

где N₂(t) и λ₂ – зависимость числа ядер ¹¹⁸In от времени и их постоянная распада. Используя формулу (2.11.6), получим

.

Таким образом,

.

Величину η_а вычислить самостоятельно (η_а = 0,7).

б) Активность препарата через время t составит

A(t) = A₁(t) + A₂(t) = λ₁·N₁(t) + λ₂·N₂(t).

Тогда

.

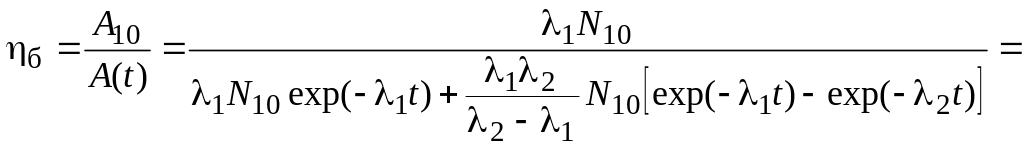
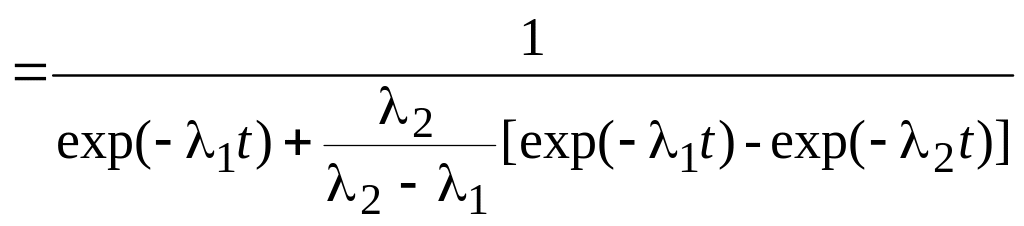Величину η_б вычислить самостоятельно (η_б = 1,85).

З адача 2.15

Определить массу свинца, который образуется из 1,0 кг ²³⁸U за время, равное возрасту горных пород (2,5·10⁹ лет).

Решение. ²⁰⁶Pb является конечным и стабильным элементом в радиоактивном семействе (ряду) урана, родоначальником которого является ²³⁸U. Поскольку суммарный период полураспада всех последующих звеньев семейства много меньше, чем период полураспада ядер ²³⁸U, то с хорошей точностью можно считать, что период полураспада, приводящий к образованию ядер ²⁰⁶Pb, равен периоду полураспада ²³⁸U.

Искомая масса ²⁰⁶Pb будет равна

M(206Pb) = Мат(206Pb)·N(206Pb) = Мат(206Pb)· Np(238U),

(2.15.1)

где N_p(²³⁸U) – количество распавшихся ядер ²³⁸U за время t, которые, в конечном итоге, превратились в равное количество ядер ²⁰⁶Pb. Если первоначальное количество ядер ²³⁸U равнялось

,

то количество распавшихся ядер ²³⁸U за время t составит

Подставив последнее выражение в (2.15.1), получим

M(²⁰⁶Pb) = =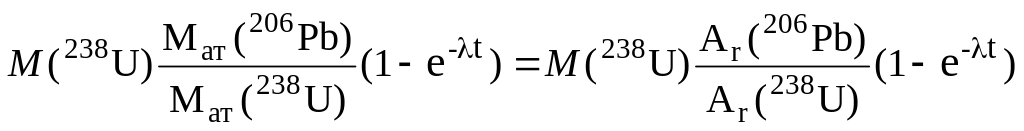 = = 0,27 кг.

З адача 2.16

Радионуклид ²⁷Mg образуется с постоянной скоростью g = 5,0·10¹⁰ ядер в секунду. Определить количество ядер ²⁷Mg, которое накопится в препарате через промежуток времени а) значительно превышающий его период полураспада; б) равный периоду полураспада.

Решение. Рассмотрим изменение dN ядер ²⁷Mg в течение малого промежутка времени dt:

dN = gdt – λNdt,

(2.16.1)

где gdt – количество рождаемых ядер, а λNdt – количество распадающихся ядер за время dt. Интегрируя это уравнение с начальным условием N(t = 0) = 0, получим формулу (2.3):

.

а) Предельный переход в (2.3) при t → ∞ дает

Полученный результат определяет максимальное количество ядер ²⁷Mg, которое может образоваться при заданных условиях.

б) Если t = T_1/2 , то выражение в скобках в (2.3) равно 1/2 и с учетом результата п. а), получим

.