
- •Введение
- •Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТИ
- •§1. Основные правила комбинаторики
- •2. Правило умножения
- •3. Выборки
- •§2. Классическое определение вероятности
- •§3. Операции над событиями
- •§4. Формула полной вероятности. Формула Бейеса
- •2. Локальная теорема Муавра – Лапласа
- •3. Интегральная теорема Муавра – Лапласа
- •4. Теорема Пуассона
- •§7. Важнейшие примеры распределений
- •1. Биномиальное распределение
- •2. Нормальный закон распределения
- •3. Распределение Пуассона
- •4. Равномерное распределение вероятностей
- •5. Геометрическое распределение
- •6. Показательное распределение
- •Индивидуальные задания
- •Глава 2. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- •§ 1. Задачи математической статистики
- •§ 2. Выборка из генеральной совокупности. Вариационный ряд. Гистограмма относительных частот
- •§ 3. Эмпирическая функция распределения
- •§ 4. Числовые характеристики статистического распределения: выборочное среднее, дисперсия
- •§ 5. Статистическая проверка статистических гипотез
- •§ 7. Примеры проверки гипотез о законе распределения выборочных данных
- •§9. Критерий равенства двух дисперсий
- •§ 10. Случайные ошибки. Законы распределения случайных ошибок в измерительных приборах
- •§11. Критерии для отбрасывания резко выделяющихся результатов испытаний
- •Приложение 1
- •Приложение 2
- •Приложение 3
- •Приложение 4
- •Приложение 5
- •Приложение 6
P 1 0,8664 0,1336 .
|
б) P( |
|
x M(Х) |
|
) 2Ф( |
|
) 0,97; |
|
Ф( |
|
) 0,485, |
|
|
2,17 |
|||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
(см. прил. 2),т.к. 2,17 2,17 |
0,2 |
0,434(см). |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
ледовательно, с вероятностью 0,97 можно гарантировать раз- |
||||||||||||||||||||||||||||||||||||||||
|
меры 15 0,434(см). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
3. Распределение Пуассона |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Как |
|
закон Гаусса, |
распределение Пуассона может быть полу- |
|||||||||||||||||||||||||||||||||||||
Счено как ас мптот ческое для биноминального. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
Рассмотр м случай, когда вероятность р положительного исхода |
||||||||||||||||||||||||||||||||||||||||
|
каждого |
спытан |
я в |
|
из п испытаний равна λ/n, где λ – некото- |
||||||||||||||||||||||||||||||||||||
|
рая постоянная вел ч на, |
|
укажем в этом случае новую приближен- |
||||||||||||||||||||||||||||||||||||||
|
ную формулу для |
Pn (к). Пусть в серии из n испытаний вероятность |
|||||||||||||||||||||||||||||||||||||||
|
серии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
появлен я |
|
|
|
я А в каждом испытании равна λ/n. Тогда вероят- |
||||||||||||||||||||||||||||||||||||
|
ность появлен я |
|
|
|
|
я А в этой серии к раз при большом n выража- |
|||||||||||||||||||||||||||||||||||
|
ется приближенной формулой (см. §5) |
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
событ |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
(1.53) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рn (к) |
|
|
к! |
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Пусть теперь Х – дискретная случайная величина, которая мо- |
||||||||||||||||||||||||||||||||||||||||
|
жет принимать целые неотрицательные значения. Если вероятность |
||||||||||||||||||||||||||||||||||||||||
|
равенства Х=к определяетсяАформулой (1.53), то мы говорим, что ве- |
||||||||||||||||||||||||||||||||||||||||
|
личина Х распределена по закону Пуассона. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Запишем закон распределения в виде табл. 1.13. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.13 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|||||||||||||||||||||||
|
хi |
|
0 |
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
к |
|
|
… |
|
|
||||||||
|
pi |
|
е |
-λ |
|
|
е |
|
|
|
|
2 е |
|
|
|
… |
|
|
|
|
к е |
|
… |
|
|
||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к! |
|
|
|
|
|
|||||||||
|
Легко проверить, что |
|
|
|
к |
|
|
|
И |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
рк |
|
|
|
е е |
1. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
к 0 |
|
|
|
|
|
к 0 к! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Для математического ожидания имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
М(Х)=0· е-λ +1· |
|
е +2· |
2 |
|
е +…+к· |
к |
е +…= |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
к! |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
68
=λ е-λ(1+ |
|
+ |
2 |
+…+ |
к 1 |
|
+…). |
1 |
|
(к 1)! |
|||||
|
2! |
|
|
||||
Но, как известно, ряд в скобках представляет разложение функции еλ в ряд Маклорена. Поэтому математическое ожидание равно
e-λ·λ·eλ или |
|
М(Х)= λ. |
(1.54) |
Мы выяснили, таким образом, вероятностный смысл параметра λ, входящего в закон распределения Пуассона: параметр λ равен ма-
темат ческому ож данию случайной величины. |
|
|
водит |
|
|
Нетрудно показать, что дисперсия случайной величины, распре- |
||
Сделенной по закону Пуассона, равна математическому ожиданию. |
||
|
D(X)=λ, |
(1.55) |
т. е. в этом случае д сперсия равна математическому ожиданию. |
||
работу |
|
|
К случайным вел чинам, подчиненным закону Пуассона, при- |
||
большое ч сло задач, относящихся к вопросам массового об- |
||
служиван я. |
|
|
В качестве пр мера укажем |
телефонной станции. Можно |
|
А |
|
|
доказать, что при выполнении некоторых условий вероятность к вы- |
||
зовов за промежуток времени длины t определяется формулой |
|
|
Рк t at к |
е at . |
(1.56) |
к! |
|
|
Если положить at=λ, то из формулы (1.56) следует, что случай- |
||
ная величина Х распределена по закону Пуассона. |
|
|
Задача 4. Среднее число вызовов, поступающих на АТС в одну |
||
минуту, равно двум. Найти вероятности того, что за 5 минут поступит |
||
2 вызова. |
|
|
|
И |
Решение. По условию, а = 24 t = 5; к = 2. Воспользуемся форму- |
||||
лой (1.56) |
|
Д |
||
Р2 |
5 |
2 5 2 |
е 25 |
0,000225. |
|
||||
|
2! |
|
|
|
Это событие практически невозможное.
4. Равномерное распределение вероятностей
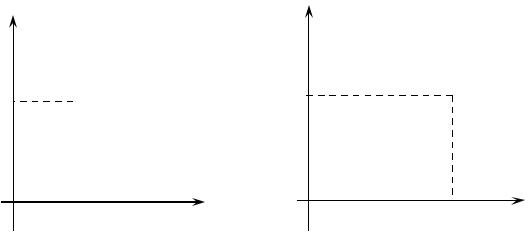
Пусть плотность вероятности равна нулю всюду, кроме интервала (а, b), на котором она постоянна. Если обозначить эту постоянную через А, то в силу свойств плотности распределения получим
69
b
Аdx 1,
a
откуда А = 1/(b–a). Поэтому плотность распределения (дифференциальный закон) равномерного распределения задается формулой
С |
|
|
0 |
при - x a; |
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
f (x) |
|
|
|
при |
a x b; |
(1.57) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
b a |
b x |
|
|
|
|||||||
|
|
|
|
|
|
|
|
0 |
при |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рис |
|
|
|
|
|
|
|
||||||||||||
( . 1.17). В точках х=а и |
х=b функция f(x) разрывна. Для нахожде- |
||||||||||||||||||
ния функц распределения (интегрального закона распределения), |
|||||||||||||||||||
воспользовавш сь формулой F(x) |
x |
|
|
|
|||||||||||||||
f (x)dx, получим [6] |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
f(бАх) |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
при |
- x a, |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(x) |
x а |
при |
a x b, |
(1.58) |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
b a |
при |
b x |
|
|
|
||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 1.18). Эта функция непрерывна всюду. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(х) |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
И |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
b a |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
а |
|
|
b |
|
|
|
|
|
|
|
|
a |
b |
||
Рис. 1.17. График функции плотно- |
Рис. 1.18. График функции распределе- |
||||||||||||||||||
сти распределения |
|
|
|
|
|
|
|
|
ния |
|
|
|
|||||||
|
Пользуясь |
формулой |
|
M Х |
|
математического |
|||||||||||||
|
|
xf (x)dx,для |
|||||||||||||||||
ожидания получим
70
|
|
|
|
b |
|
x |
|
|
|
a b |
|
|
|
|
|
|||||||
|
|
M(x) |
|
|
|
|
dx |
|
|
|
|
|
, |
|
|
|
|
|
(1.59) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
a b a |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
так что математическое ожидание случайной величины, равномерно |
||||||||||||||||||||||
распределенной на интервале (а, b), находится в центре этого интер- |
||||||||||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пользуясь форму- |
||||
вала. Для вычисления дисперсии найдем M (X 2 ), |
||||||||||||||||||||||
лой (1.32) |
|
M Х 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x2 f (x)dx: |
|
|
|
|
|
|||||||||||||||
личины3 |
|
|
|
2 |
|
|
12 |
|
|
|
|
|
||||||||||
|
|
b x2 |
|
|
|
|
b3 a3 |
|
|
а2 ab b2 |
|
|
||||||||||
M(Х 2) a |
|
dx |
|
|
|
|
|
|
|
|
. |
|
(1.60) |
|||||||||
b a |
3 b a |
3 |
|
|
|
|||||||||||||||||
Поэтому д сперс я равномерно распределенной случайной ве- |
||||||||||||||||||||||
по формуле D X M |
X |
2 |
M X 2 |
равна |
|
|
|
|
|
|||||||||||||
образом |
|
|
|
b a 2 |
|
|
||||||||||||||||
|
|
а2 ab b |
2 |
|
|
(a b)2 |
|
|
|
|
|
|||||||||||
D(X) |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
(1.61) |
|||||||
Так м |
, для случайной величины, равномерно распреде- |
|||||||||||||||||||||
|
А |
|
|
|||||||||||||||||||
ленной на нтервале (а, b), среднее квадратическое отклонение равно |
||||||||||||||||||||||
0,288675… длины интервала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пользуясь формулой, для определения вероятности попадания |
||||||||||||||||||||||
непрерывной случайной величины X на участок от до получим |
||||||||||||||||||||||
|
|
P( X ) F( ) F( ). |
|
|
|
|
(1.62) |
|||||||||||||||
|
|
|
|
|
|
|
Д |
|
||||||||||||||
Задача 5. Точка бросается наугад (без прицеливания) на отрезок |
||||||||||||||||||||||
[0,I]. Случайная величина Х–абсцисса точки попадания (считается, |
||||||||||||||||||||||
что бросаемая точка обязательно попадает на отрезок [0, 1]). Найти |
||||||||||||||||||||||
функцию плотности распределения и функцию распределения. Вы- |
||||||||||||||||||||||
числить математическое ожидание и дисперсию указанной случайной |
||||||||||||||||||||||
величины. Найти вероятность того, что точка попадет в интервал |
||||||||||||||||||||||
[0; 0,5]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. В этом случае мы имеем дело с непрерывной случай- |
||||||||||||||||||||||
ной величиной, все значения которой принадлежат отрезку [0, 1]. По- |
||||||||||||||||||||||
этому в выражении для плотности распределения и функции распре- |
||||||||||||||||||||||
деления, а = 0, а b = 1, т. е. |
|
0; |
|
|
|
|
|
|
|
|
И |
|||||||||||
0 |
при - x |
|
|
|
|
|
0 при - x |
0; |
|
|||||||||||||
|
при |
0 x 1; |
|
|
|
|
|
|
х при |
0 x 1; |
|
|||||||||||
f (x) 1 |
|
|
F(x) |
|
||||||||||||||||||
|
при |
1 x ; |
|
|
|
|
|
|
|
|
|
1 x . |
|
|||||||||
0 |
|
|
|
|
1 при |
|
||||||||||||||||
Согласно формулам (1.59), (1.61) и (1.62) М(Х)=1/2, D(X) = 1/12,
P(0 х 0,5) F(0,5) F(0) 0,5 0 0,5.
71
