Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2078.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

2.92 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1914 15 16 17 18 19 > Следующая >>>

§ 7. Примеры проверки гипотез о законе распределения выборочных данных

	Пример 1. В табл. 2.8 приведен вариационный ряд значений ло-
гарифма долговечности образцов диаметром 8 мм из алюминиевого
С
сплава		АВ, испытанных на консольный изгиб с вращением при на-
пряжении σmax=15 кгс/мм2.
1.			остав ть выборочное распределение.
	2. Постро ть г стограмму и график выборочной функции рас-
двинуть
пределен			я.
	3. Найти состоятельные несмещенные оценки для математиче-
ского ож дан я					д сперсии.
	4. Постро ть доверительные интервалы для математического
ожидан я д сперс						с уровнем доверия = 0,95.
	5. На основан					анализа формы построенной гистограммы вы-
			г потезу о законе распределения и								проверить справедли-
вость г потезы по кр терию Пирсона с уровнем значимости 0,05.
												Таблица 2.8

	i	xi lg Ni			i	xi lg Ni		i	xi lg Ni		i	xi lg Ni

	1	5,8669			26	6,3310		51	6,5224		76	6,7275
	2	5,9164			27	6,3688		52	6,5431		77	6,7275
	3	6,0216			28	6,3746		53	Д
	3	6,0216			28	6,3746		53	6,5464		78	6,7392
	4	6,0386			29	6,3811		54	6,5578		79	6,7432
	5	6,0426		бА30 6,3829 55 6,5603 80								6,7538
	6	6,0445			31	6,3829	56		6,5607		81	6,7809
	7	6,0645			32	6,3918	57		6.5654		82	6,7975
	8	6,0799			33	6,3967	58		6.5655		83	6,7975
	9	6,0821			34	6,4076	59		6,5793		84	6,7988
	10	6,1062			35	6,4089	60		6,5823	И
	10	6,1062			35	6,4089	60		6,5823		85	6,8038
	11	6,1082			36	6,4094	61		6,5916		86	6,8142
	12	6,1183			37	6,4216	62		6,5957		87	6,8169
	13	6,1186			38	6,4328	63		6,6096		88	6,8649
	14	6,1238			39	6,4342	64		6,6471		89	6,8717
	15	6,1605			40	6,4620	65		6,6474		90	6,8977
	16	6,1685			41	6,4630	66		6,6739		91	6,9051
	17	6,1746			42	6,4646	67		6,6739		92	6,9109
	18	6,1801			43	6,4704	68		6,6780		93	6,9189
	19	6,1892			44	6,4713	69		6,6896		94	6,9299
	20	6,1951			45	6,4842	70		6,6916		95	6,9545
	21	6,2071			46	6,4975	71		6,7000		96	7,0824
	22	6,2100			47	6,4984	72		6,7086		97	7,1682
	23	6,2297			48	6,5179	73		6,7132		98	7,2603
	24	6,2608			49	6,5201	74		6,7178		99	7,2775
	25	6,3115			50	6,5214	75		6,7197		100	7,4586

162

Решение

1. Сначала построим ранжированный ряд. В табл. 2.8 случайные

	величины уже представлены в виде ранжированного ряда. Ранжиро-
	ванный ряд – это перечень отдельных единиц совокупности в порядке
	возрастания (убывания) изучаемого признака (см. табл. 2.8).
С						2							2
		Для построения интервального вариационного ряда выполняем
	следующие действия:
		1. Дл на част		чного интервала задана и равна 10.
							хi хi 1 i ,
	Очевидно
	где i 0,1, ,n; х			х			; х		n	х				.
			0		min				n		max
		2. Подсч таем ч сло элементов (частот) выборки, попадающих
	в каждый нтервал.							, n1		n2		... nk 100.
		бА
		Стро м нтервальный статистический ряд (табл. 2.9).
														Таблица 2.9
	i	Границы интервалов									Число наблюдений ni
	1	5,825 - 5,97											2
	2	5,975 - 6,12											12
	3	6,125 - 6,27											10
	4	6,275 - 6,42											13
	5	6,425 - 6,57							Д
	5	6,425 - 6,57											21
	6	6,575 - 6,72											17
	7	6,725 - 6,87											14
	8	6,875 - 7,02											6
	9	7,025 - 7,17											2
	10	7,175 - 7,32											2
	11	7,325 - 7,47											1

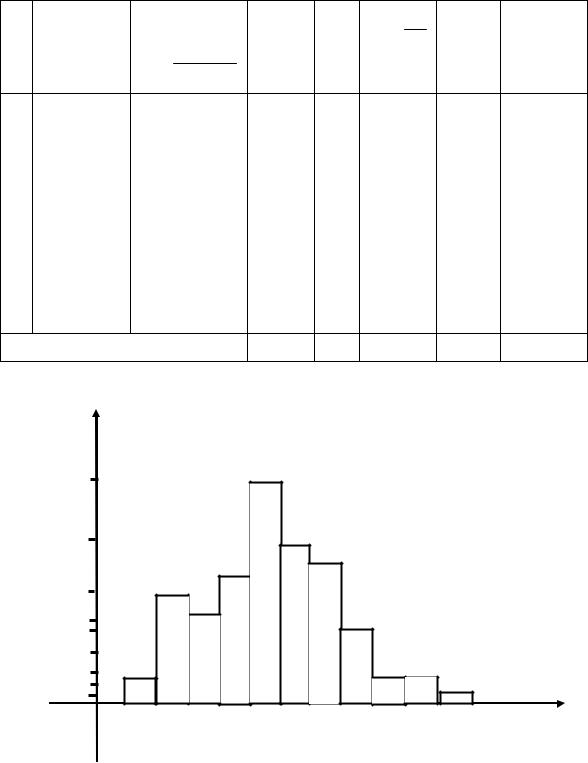
2. Построение гистограммы плотностей относительных час-

тот – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной , а высоты

равны отношению h	pi*		pi*	.	И

i		10

Полученные значения высот вносим в табл. 2.10.

163

																			Таблица 2.10
i	Границы			Середина					Число		p	*			*		*	~		~2
											p			h	*	pi		x	n	x	n
	интервалов			интервала				наблю-			i			h				i	i	i	i
	интервалов			интервала				наблю-						i
	хi; хi 1		~			xi xi 1			дений
			xi			2				ni
						2				ni
1	5,825;5,97				5,90					2	0,02				0,13			11,80		69,6200
2	5,975;6,12				6,05					12	0,12					0,8		72,60		439,2300
3	6,125;6,27				6,20					10	0,10				0,67			62,00		384,4000
4	6,275;6,42				6,35					13	0,13				0,86			82,55		524,1925
5	6,425;6,57				6,50					21	0,21					1,4		136,50		887,2500
6	6,575;6,72				6,65					17	0,17				1,13			113,05		751,7825
С					6,80					14	0,14				1,08			95,20		647,3600
7	6,725;6,87				6,80					14	0,14				1,08			95,20		647,3600
8	6,875;7,02				6,95					6	0,06					0,4		41,70		289,8150
9	7,025;7,17				7,10					2	0,02				0,13			14,20		100,8200
10	7,175;7,32				7,25					2	0,02				0,13			14,50		105,1250
11	7,325;7,47				7,40					1	0,01				0,07			7,40		54,7600
и
	Сумма							100			1,00							651,50		4254,3550
	Строим гистограмму по данным 6-го столбца табл. 2.10.
			hi٭∙100
	1,4	бА
		бА
	1,13									Д
	0,8
	0,67
	0,1
	0,07
			1		2	3	4		5	6	7		8			9	10	11
						3	4		5							И
																					х
		Рис. 2.6. Гистограмма плотностей относительных частот

164

По виду гистограммы (рис. 2.6) подбираем подходящий для данного случая теоретический закон распределения.

равниваем гистограмму с теоретическими кривыми основных законов (нормальный, показательный, равномерный). По виду гистограммы можно выдвинуть гипотезу о нормальном законе распределения случайной величины X.

3. Нахождение состоятельных несмещенных оценок матема-

тического ож дан я

дисперсии. Найдем оценки математического

ожидан я а

д сперс

651,5

Са x

i 1

6,515;

100

)

бА

4254,355

Dв

xв

6,515

100

n i 1

0,09823,

т.е.

1 l

xв

0,09823.

ni 1

Согласно определению исправленной выборочной дисперсией

называется произведение выборочной дисперсии на величину

т.е. исправленная дисперсия равна

n 1

100

0,09823

0,09922 ,

а исправленное

выборочное

среднеквадратическое

отклонение

s 0,315 .

4. Построим доверительный интервал для математического

ожидания по формуле

Ip хв t

;хв

Ввиду большего объема выборки можноИсчитать, что распреде-

ление Стьюдента близко к нормальному закону. По таблице значений

функции Лапласа найдем t

1,96 (см. прил. 2), тогда

0,09922

6,515 1,96

;6,515 1,96

или

165

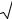
I 6,4955;5,5345 .

Доверительный интервал для дисперсии построим по формуле s2 1 q 2 D s2 1 q 2 при q<1;

0 D s2 1 q 2 при q>1.

Найдем доверительный интервал для D при заданной надежно-

сти = 0,95. По прил. 5 находим q (n = 100; = 0,95) = 0,143. Следо-

вательно, гран цы доверительного интервала:

0,09922(1– 0,143)2 = 0,0729 и 0,09922(1+0,143)2 = 0,1134.

совокупности

Итак, 1,0729 <

D <0,1134 с вероятностью 0,95.

5. В д г стограммы позволяет выдвинуть гипотезу о нормаль-

Сном законе распределен я исследуемой случайной величины Х.

Провер м г потезу о нормальном распределении генеральной

бА

по кр терию Пирсона. В качестве меры расхождения

между теорет ческ м распределением

f (x)и эмпирическим распре-

делением

f (x)

спользуем статистику 2

npi

, где n –

i 1 npi

число опытов;

pi – вероятность попадания возможных значений слу-

чайной величины в i-й разряд статистического ряда; l– число разря-

дов.

Так как выдвинута гипотеза в пользу нормального закона рас-

пределения генеральной совокупности, теоретические вероятности

находим по формуле

i 1

pi P(xi

xi 1) Ф

где

Ф(x)

2 0 e

–

функция Лапласа (см. прил.2);

i 1,2, ,12.

Имеем

в 240,5;

19,8.

хi

Обозначим через

xв

затем

определим

теоретические

вероятности pi

и теоретические частоты ni

pi n, для чего составим

расчетную табл. 2.11.

По условию, объём выборки n =100, значения случайной вели-

чины разбиты на 11 интервалов. Так как частоты

попадания в каж-

166

дый из первого и трех последних интервалов малы (меньше 5), объединяем их соответственно в первый и последний. Вычисление в2 приведено в табл. 2.11. Элементы 5-го столбца определяем по прил.2,

вероятности рi – элементы 6-го столбца –

вычисляются следующим

образом:

Ф 0,3925 0,5 0,0053;

P( X

6,125) Ф 1,24

P(6,125 X 6,275) Ф 0,76 Ф 1,24 0,2764 0,3925 0,1161;

;

0,0734;

P(6.875

X 7,025)

Ф 1,61 Ф 1,14 0,4463 0,3729

P(7,025 X ) Ф Ф 1,61 0,5 0,4463 0,0537.

бА

Таблица 2.11

Границы

Координа-

Значение функ-

Оцен-

npi

n i npi 2

интерва-

ты

границ

ции Лапласа на

ка

ве-

npi

лов хi;хi 1

интервалов

границах интер-

роят-

в долях

вала.

ности

относи-

Ф zi

попа-

тельно

дания

хвыб ,

ин-

xi x

выб

тервал

5,825÷5,975

–∞ ÷ -1,71

5,975÷6,125

–1,71÷-1,24

- 0,5 0,4564

- 0,4564 0,3925

6,125÷6,275

–1,24-÷-0,76

–0,3925÷–0,2764

0,1161

11,61

0,223

6,275÷6,425

–0,76÷–0,29

–0,2764÷-0,1141

0,1623

16,23

0,643

6,425÷6,575

–0,29÷0,19

–0,1141÷0,0753

0,1894

18,94

0,224

6,575÷6,725

0,19÷0,67

0,0753÷0,2486

0,1733

17,33

0,006

6,725÷6,875

0,67÷1,14

0,2486÷0,3729

0,1243

12,43

0,198

6,875÷7,025

1,14÷1,61

0,3729÷0,4463

0,0734

7,34

0,244

7,025÷7,175

1,61÷2,09

0,4463 0,4817

7,175÷7,325

2,09÷2,57

0,0537

5,37

0,025

2 5

0,4817 0,4949

7,325÷7,475

2,57÷∞

0,4949 0,5

Сумма

–

1,000

100

в =2,

547

167

Найдем меру расхождения между теоретическим распределением и эмпирическим распределением по формуле

npi

i 1

Для эгого суммируем элементы 8-го столбца табл. 2.11 и полу-

чим

в2.

2,547 .

npi

i 1

огласно теореме Пирсона при n распределение величины

С2

деления

зав с т от параметра k , который называют числом степеней сво-

боды. k = l – 1 – r, где r – число параметров предполагаемого распре-

свободы

, оцененных по данным выборки; l – число интервалов. Число

степеней

k 8 1 2 5.

Выберем уровень

значимости

0,05

по та л це квантилей

– распределения для числа сте-

пеней свободы k 5

уровня значимости 0,05

(см. прил. 4)

найдем критическое значение

(0,05;5) 11,1; так как наблюденное

кр

значение оказалось меньше та личного значения, то можно сделать
вывод: выдвинутая гипотеза о нормальном законе распределения не
противоречит опытным данным. Следовательно, гипотезу о нормаль-
							Д
ном распределении генеральной совокупности принимаем.
		Пример 2. Для определения надежности металлорежущих стан-
ков на заводе фиксировались значения наработки на отказ (время τ
непрерывной работы до первого отказа). Полученные данные для τ (в
месяцах) приведены в табл. 2.12.									И
											Таблица 2.12
	3,0		3,6	4,4	1,3	2,1		5,0	4,9	6,0	1,1	2,3
	5,9		3,6	1,3	3,7	4,9		5,6	1,3	2,0	4,3	1,9
	4,0		3,7	5,3	4,2	2,5		2,7	3,6	4,8	6,0	1,7
	2,5		4,9	3,2	4,0	4,3		2,8	3,8	1,0	4,2	4,8
	4,9		5,0	1,9	2,6	1,7		6,0	5,7

1.Составить выборочное распределение.

2.Построить гистограмму и график выборочной функции распределения.

3.Найти состоятельные несмещенные оценки для математиче-

168

ского ожидания и дисперсии.

4. Построить доверительные интервалы для математического ожидания и дисперсии с уровнем доверия р = 0,95.

5. На основании анализа формы построенной гистограммы выдвинуть гипотезу о законе распределения и проверить справедливость

Сния ед ц совокупности по возрастающим (чаще) или по убывающим (реже) значен ям признака и подсчет числа единиц с тем или значен ем пр знака. Для этого сначала построим ранжирован-

гипотезы по критерию Пирсона с уровнем значимости 0,05.

Решение

1. Первым этапом статистического изучения вариации явля-

ются построен е вар ационного ряда – упорядоченного распределе-

иным2.13).

ный ряд.

Ранж рованный ряд – это перечень отдельных единиц совокупности в порядке возрастания (у ывания) изучаемого признака (табл.

Таблица 2.13

xi	1,0	1,1	1,3	1,7	1,9	2,0	2,1	2,3	2,5	2,6	2,7	2,8
ni	1	1	3	2	2	1	1	1	2	1	1	1
xi	3,0	3,2	3,6	3,7	3,8	4,0	4,2	4,3	4,4	4,8	4,9	5,0
ni	1	1	3	2	1	2	2	2	1	2	4	2
хi	5,3	5,6	5,7	5,9	6,0
		бА
ni	1	1	1	1	3

Интервальным вариационнымДрядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с соответствующими частотами или частностями попаданий в ка-

ждый из них значений величины.

Для его построения выполняем следующие действия: 1. Найдем размах выборки

R xmax xmin.			И
Имеем R 6,0 1,0 5,0.

2. Определим длину частичного интервала. – шаг разбиения
по формуле Стерджеса:	R	R
			,
	1 3,322lgn
		k

где n – объём выборки; k – число частичных интервалов. Так как

169

n 47, то	k 1 3,322 log 47	7 ;		5	0,7.

			7

хi хi 1 i ,

где i 0,1, ,n;х0

хmin

; хn

хmax

3. Подсчитаем число элементов (частот) выборки, попадающих

в каждый интервал. Очевидно, n1 n2 ... nm 47.

тро м нтервальный статистический ряд (табл. 2.14).

Элементы третьей строки называются относительными часто-

тами

попадан я в

нтервал. Очевидно,

...

бА

Таблица 2.14

хi; хi 1

1,0;1,7

1,7;2,4

2,4;3,1

3,1;3,8

3,8;4,5

4,5;5,2

5,2;6,0

2. Построение гистограммы плотностей относительных час-

тот.

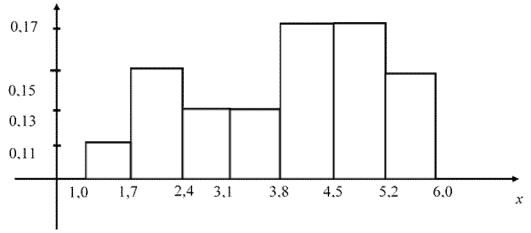
Рис. 2.7. Гистограмма относительных частот

Построим гистограмму относительных частот – ступенчатую

170

фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной 0,7, а высоты равны отноше-

нию h*			p*
				i	. Площадь всей гистограммы должна быть равна
					. Площадь всей гистограммы должна быть равна
	i
1. Гистограмма является оценкой генеральной функции плотности
f(x).
	Полученные значения высот вносим в табл. 2.15.
и																	Таблица 2.15
С
	i						*			*		~	xi xi 1	~				~	2
	i	аi		;ai 1						*		~	xi xi 1	~				~
								pi	*	pi		xi		xi		ni		xi		ni
									*	pi
						ni			hi				2
						ni			hi				2

	1	1,0;1,7				5		5	0,11			1,35		6,75				9,1125
							47
	2	1,7;2,4				7		7	0,15			2,05		14,35				29,4175
							47
	3	2,4;3,1				6		6	0,13			2,75		16,5				45,375
							47
	4	3,1;3,8				6		6	0,13			3,45		20,7				71,415
							47
	5	3,8;4,5				8	8		0,17			4,15		33,20				137,78
												Д
							47					Д
						бА
	6	4,5;5,2				8 8 0,17 4,85								38,8				188,18
								47
	7	5,2;6,0				7	7		0,15		5,6			39,2				219,52
							47
		47				1							И
		47				1								169,02				697,48
	Примечание.					*	плотность относительной частоты;							~	середина час-
	Примечание.					hi	плотность относительной частоты;							xi	середина час-

тичных интервалов;* – определяет эмпирические значения.

По виду гистограммы (рис. 2.7) подбираем подходящий для данного случая теоретический закон распределения. Для этого сравним полученную ступенчатую фигуру с теоретическими кривыми основных законов: нормальным, показательным и равномерным.

По виду гистограммы можно выдвинуть гипотезу о равномерном законе распределения случайной величины X (см. рис. 2.7).

171

Нахождение состоятельных несмещенных оценок матема-

тического ожидания и дисперсии. Найдем оценки математического

ожидания а и дисперсии D.

Основными параметрами генеральной совокупности являются

математическое ожидание (генеральная средняя) М(Х) и среднее

квадратическое отклонение s. Это постоянные величины, которые

можно оценить по выборочным данным. Оценка генерального пара-

метра, выражаемая одн м числом, называется точечной.

Точечной оценкой генеральной средней а является выборочное

Еслиl

среднее. Выборочным средним называется среднее арифметическое

всех значен й вел ч ны, встречающихся в выборке.

выборочное среднее вычисляется по несгруппированным

данным, то для его определения сумму всех значений делят на коли-

бА

чество элементов в вы орке. В данном случае определяем по сгруп-

пированным данным (см. та л. 2.15):

169,2

а xв

i 1

3,6.

)

697,48

i 1

xв

3,6

1,88,

т.е.

n i 1 i

1 l

Dв

xв

1,88.

ni 1

Согласно определению исправленной выборочной дисперсией

называется произведение выборочной дисперсии на величину

Следовательно, исправленнаяДдисперсия равна

1,88 1,92,

т.е. исправленное выборочное

среднеквадратическое

отклоне-

ниеs 1,3856 .

Построим доверительный интервал для математического

ожидания по формуле I

;х

Ввиду большого объема выборки можно считать, что распределение Стьюдента близко к нормальному закону. По таблице значений функции Лапласа найдем (см. прил. 2) t 1,96, тогда

172

			1,4								1,4		или I 3,2;4 .
Ip 3,6 1,96						; 3,6 1,96
Ip 3,6 1,96			6,8			; 3,6 1,96
			6,8									6,8
Доверительный интервал для дисперсии построим по формуле
							n 1 s			2		D			n 1 s2		.
							2					D			2		.
							2								2
						2									1
Для 1 p 1 0,95										0,05 найдем значения 12 и 22 :
P( 2 12) 1								0,975; P( 2								22)			0,25.
P( 2 12) 1								0,975; P( 2								22)			0,25.
						2											2
и
По пр л. 4 найдем
2		0,975;46 16,8;												2	0,025;46 47,0.
С		0,975;46 16,8;												2	0,025;46 47,0.
1														2
Тогда
	n 1 s2				46 1,92								n 1 s2					46 1.92
образом
	2					47,0			1,89,						2		16,8			5,2.
2															1
Так м				, доверительный интервал для дисперсии будет
иметь в д (1,89;5,2).

5. В д г стограммы позволяет выдвинуть гипотезу о равномерном законе распределения исследуемой случайной величины Х.

Найдем выравнивающую кривую. Функция плотности нормального распределения имеет вид (см. 2.10)

x a,b ;

f (x)

А, x a,b .

b a

Поскольку M(X)

a b

(X)

a b 2

D(X)

то оценки параметров a и b – концы интервала, в котором наблюда-

лись возможные значения Х, находим из системы (через a и b

обо-

значены оценки параметров)

b a xB;


b a
		B.

	2 3
	2 3

Решая систему уравнений относительно a и b , получим

;

Тогда теоретическое распределение для данных значений пара-

173

метров примет вид

0,	x a,b
	1
f (x)		, x a,b ,

	a
b

где

3,6

1,3856 1,18;

3,6

1,3856 5,52.

Так м образом, получено теоретическое распределение

совокупности

0, x

l ni

npi 2

1,18;5,52 ;

f (x)

0,23, x 1,18;5,52.

Провер м г потезу о равномерном распределении генеральной

по кр терию Пирсона. В качестве меры расхождения

бА

между теорет ческ м распределением f (x)

и эмпирическим распре-

делением f (x) спользуем

статистику

, где n–

i 1

npi

число опытов; pi – вероятность попадания возможных значений случайной величины в i -й разряд статистического ряда; l– число разрядов.

Теоретические вероятности находим по формуле

				xi				xi					1			Д
pi			x	f (x)dx							b a				dx;
			x	i 1				x	i 1		b a
				i 1					i 1
			х2				1,7										1,181,7 0,1196;
p1			0,23dx 0,23dx 0,23x
p1			0,23dx 0,23dx 0,23x
			а				1,18							2,4
														2,4						2.4 0,161;
p	2	p			p	4	p			p		6		0,23dx 0,23x						2.4 0,161;
	2			3		4	5					6		1,7						1.7
																				1.7

			b				5,52											55,,522 0,0736.
p7					0,23dx					0,23dx 0,23x								55,,522 0,0736.
			xn 1				5.2												ИТаблица 2.16
Вычисления сведем в табл. 2.16.

xi ;xi 1			1.0;1.7					1.7;2.4					2.4;3.1						3.1;3.8	3.8;4.5	4.5;5.2	5.2;6.0
ni			5					7					6						6	8	8	7
pi			0,1196					0,161					0,161						0,161	0,161	0,161	0.0736

174

Окончание табл. 2.16

npi		5.6212	7.567	7.567	7.567	7.567	7.567	3.4592
ni npi		-0.6212	-0.567	-1.567	-1.567	0.433	0.433	3.5408
ni	npi 2	0.38	0.32	2.46	2.46	0.19	0.19	12.53

		выб2			0,38		0,32		2,46				2,46				0,19		0,19			12,53		4,44.
							7,56		7,56
				5,62								7,56				7,56		7,56		3,45
			огласно теореме Пирсона при n распределение величи-
	ны	2 зав с т от параметра										k , который называют числом степеней
	Число
	свободы. k = l – 1 – r, где r – число параметров предполагаемого рас-
Спределен я, оцененных по данным выборки: l – число интервалов.
			степеней сво оды k 7 1 2 4. Выберем уровень значимости
	0,05			табл
				по			це квантилей							2–		распределения для числа степе-
	ней свободы k 4							уровня значимости 0,05 ( см. прил. 4) най-
	дем кр т ческое значение										2	(0,05;4) 9,5; так как наблюденное зна-

	чение оказалось меньше та личного значения, то можно сделать вы-
								А
	вод: выдвинутая гипотеза о равномерном законе распределения не
	противоречит опытным данным. Следовательно, гипотезу о равно-
	мерном распределении генеральной совокупности принимаем.
		Пример 2. Произведен вы ор 100 проволок и проведены испы-
														Д
	тания их на прочность. В табл. 2.17 приведены разрывные усилия
	проволок (Н/мм2), полученные при испытаниях.
		Первоначальную длину интервала при группировке взять рав-
	ной 10 Н/мм2.																							Таблица 2.17

	221		233			175		215		235					260						И
																		201			234		211		237
	200		254			245		207		243					251			210			245		250		223
	223		265			285		239		195					250			245			227		231		256
	244		213			257		243		225					242			254			238		241		261
	248		275			224		273		243					282			235			264		280		248
	251		212			247		198		232					233			236			244		225		234
	240		237			235		258		241					233			232			263		305		243
	223		231			253		201		233					231			220			245		255		219
	262		251			250		215		228					257			229			221		244		284
	252		245			265		232		248					221			242			226		247		239

1.Составить выборочное распределение.

2.Построить гистограмму и график выборочной функции распределения.

175

3.Найти состоятельные несмещенные оценки для математического ожидания и дисперсии.

4.Построить доверительные интервалы для математического

	ожидания и дисперсии с уровнем доверия =0,95.
		5. На основании анализа формы построенной гистограммы вы-
С										проверить справедли-
	двинуть гипотезу о законе распределения и									проверить справедли-
	вость гипотезы по критерию Пирсона с уровнем значимости 0,05.
		Решен е
		1.	начала постро м ранжированный ряд. Ранжированный ряд –
	признака
	это перечень отдельных единиц совокупности в порядке возрастания
	(убыван		я) зучаемого				(табл. 2.18).					Таблица 2.18
												Таблица 2.18
	xi	175		195	бА						211	212	213
	xi	175		195	198	200	201	207	210		211	212	213
	ni	1		1	1	1	1	1	1		1	1	1
	xi	215		219	220	221	223	224	225		226	227	228
	ni	2		1	1	3	3	1	2		1	1	1
	xi	229		230	231	232	233	234	235		237	238	239
	ni	1		1	3	3	4	2	3		3	1	2

	xi	240		241	242	243	Д					247	248
	xi	240		241	242	243	245	247	244	245		247	248
	ni	1		2	2	4	5	2	3	5		2	3
	xi	248		250	251	252	253	254	255	256		257	258
	ni	2		2	1	1	1	2	И
	ni	2		2	1	1	1	2	2	1		1	1
	xi	260		261	262	263	264	265	273	275		280	282
	ni	1		2	1	1	1	2	1	1		1	1
	xi	284		305	–	–	–	–	–		–	–	–

	ni	1		1	–	–	–	–	–		–	–	–

Для построения интервального вариационного ряда выполняем следующие действия:

1. Длина частичного интервала задана и равна 10.

176

хi хi 1 i ,

	где i 0,1, ,n; х0						хmin						;	хn хmax								.
	где i 0,1, ,n; х0						хmin				2		;	хn хmax					2			.
				2. Подсчитаем число элементов (частот) выборки, попадающих
	в каждый интервал. Очевидно, n1 n2																... nk 100.
С
					троим интервальный статистический ряд (табл. 2.19).
																													Таблица 2.19
	хi	;хi 1			180;190		190;200						200;210					210;220								220;230						230;240
	и																															22
	ni				1		2						3					7								14						22
				ni	0,01		0,02						0,03					0,07								0,14						0,22
	i			n
	х	;х			бА* *																					280;290						290;300
	х	;х			240;250		250;260						260;270					270;280								280;290						290;300
	i			i 1									260;270
	ni				22		15					8						2								3						1
				ni	0,22		0,15					0,08						0,02								0,03						0,01
	i			n
				2. Построение гистограммы плотностей относительных час-
	тот –				ступенчатая фигура, состоящая из прямоугольников, основа-
																Д
	ниями которых служат частичные интервалы длиной																											, а высоты
	равны отношению h									pi	pi .
							i					10
				Полученные значения высот вносим в табл. 2.20.																									Таблица 2.20
																													Таблица 2.20

									*						p*					x	i		x		1							2
			аi;ai 1									*				i	~				i			i	1		~		~
	i							p				h					xi						2				x n			x		n
	i							p				h					xi										x n			x		n
						ni		i					i														i	i			i		i
	1		180;190			1		0,01				0,001					185										185		34225
	2		190;200			2		0,02				0,002					195										390		76050
																											И
	3		200;210			3		0,03				0,003					205										615 126075
	4		210;220			7		0,07				0,007					215										1505		323575
	5		220;230			14		0,14				0,014					225										3150			708750
	6		230;240			22		0,22				0,022					235										5170			1214950
	7		240;250			22		0,22				0,022					245										5390			1320550

177

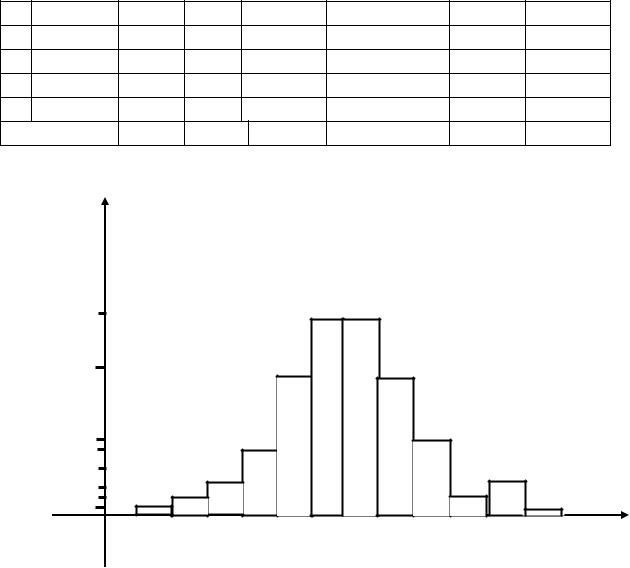
											Окончание табл. 2.20
8	250;260		15		0,15	0,015		255			3825		975375
9	260;270		8		0,08	0,008		265			2120		561800
10	270;280		2		0,02	0,002		275			550		151250
11	280;290		3		0,03	0,003		285			855		243675
12	290;300		1		0,01	0,001		295			295		87025
			100		1						240500		5823300
	тро м г стограмму по данным 5-го столбца табл. 2.20.
				hi٭∙100
С
	2,2
и
	1,5	бА
	1,4
	0,8
	0,7
	0,3
	0,1
													290300
			180	190	200	210	220 230	240	250	260	270	280	290300	х
	Рис. 2.8. Гистограмма плотностей относительных частот
							Д
	По виду гистограммы (рис. 2.8) подбираем подходящий для
данного случая теоретический закон распределения.
	Сравниваем гистограмму с теоретическими кривыми основных
законов (нормальный, показательный, равномерный). По виду гисто-
граммы можно выдвинуть гипотезу о нормальномИзаконе распределе-
ния случайной величины X.
	3. Нахождение состоятельных несмещенных оценок матема-
тического ожидания и дисперсии. Найдем оценки математического
ожидания а и дисперсии D.

178

24050

i 1

240,5;

l ~

100

)

i 1

1 l

5823300

n x

xв

240,5

100

ni 1

i i

392,75, т.е.

n x

xв

392,75.

ni 1 i

исправленная

огласно определению исправленной выборочной дисперсией

называется про зведен е вы орочной дисперсии на величину

n 1

т.е.

бА

сперсия равна

100

392,75 396,7,

а исправленное

вы орочное

среднеквадратическое отклонение

s 19,8173 .

Построим доверительный интервал для математического

ожидания по формуле Ip

хв t

;хв t

Ввиду большего объема выборки можно считать, что распреде-

ление Стьюдента близко к нормальному закону.

По таблице значений

функции Лапласа найдем t

1,96 (см. прил. 2), тогда

19,8

240,5 1,96

;240,5 1,96

или I 236;244 .

Доверительный интервал для дисперсии построим по формуле

s2 1 q 2

D s2 1 q 2

при q<1;

0 D s2 1 q 2

при q>1.

Найдем доверительный интервал для D при заданной надежно-

сти = 0,95. По прил. 5 находим q (n = 100;

И= 0,95) = 0,143. Следо-

вательно, границы доверительного интервала: 396,7(1– 0,143)2

= 293,1

и 396,7(1+0,143) = 518,27.

Итак, 293,1 < D < 518,27 с вероятностью 0,95.

5. Вид гистограммы позволяет выдвинуть гипотезу о нормальном законе распределения исследуемой случайной величины Х.

Проверим гипотезу о нормальном распределении генеральной

179

совокупности по критерию Пирсона. В качестве меры расхождения между теоретическим распределением f (x)и эмпирическим распре-

				2	l	n np		2
делением f		(x) используем статистику				i	i		, где n –

					i 1 npi
число опытов; pi – вероятность попадания возможных значений слу-
чайной величины в i-й разряд статистического ряда;							l– число разря-
дов.
Так как выдв нута гипотеза в пользу нормального закона рас-
пределен я	генеральной совокупности,		теоретические					вероятности

	наход м по формуле
С
С																x				xв					x x					в
		pi P(xi																i 1										i		в

					X xi 1) Ф														в					Ф				в					,
																			в									в
	где Ф(x)			1			t		t2	dt– функция Лапласа (см. прил.2); i 1,2, ,12.
				1			e	2
							e	2
	и
		Имеем		2	0
		Имеем											в 240,5;
												x	в 240,5;								в 19,8.
														хi
		Обозначим через zi												хi					xв	,		затем			определим теоретические
																в
	вероятности pi					и теоретические частоты ni																					pi		n,			для чего составим
	расчетную табл. 2.21.
			бА																															Таблица 2.21
																																		Таблица 2.21

	i	хi;хi 1					ni				zi					Ф zi								рi				ni pi n							n i n 2
																												pi		100						i
																																			ni
																																			ni
																							Д
	1	2			3						4						5						6							7				8
	1	180;190					1										-0,5						0,0053						0,53					0,0047
							2 6																								6,17
	2	190;200					2 6				-2,55				-0,4947								0,0154						1,54		6,17

	3	200;210									-2,04				-0,4793								0,0411
							3																						4,11
	4	210;220			7						-1,54				-0,4382								0,0897						8,97					0,4327
		210;220																								И
	5	220;230			14						-1,03				-0,3485								0,1466						14,66					0,0297
	6	230;240			22						-0,53				-0,2019								0,1899						18,99					0,4502
	7	240;250			22						-0,03				-0,0120								0,1964						19,64					0,2836
	8	250;260			15						0,48					0,1844							0,1521						15,21					0,0029

180

Окончание табл. 2.21

	9	260;270			8		0,98				0,3365				0,0954				9,54				0,2486
	10	270;280			2		1,49				0,4319				0,0448				4,48				0,963
	11	280;290			3 6		1.99				0,4767				0,0171				1,71		6,81

	12	290;300					2,5				0,4938				0,0062
					1														0,62
											0,5
С				100			1													100			в2 1,5487
							1													100			в2 1,5487

	прилвероятности.2, – элементы 6-го столбца –																					вычисляются сле-
		По услов ю, объём выборки n=100, значения случайной

	величины разб ты на 12 интервалов. Так как частоты ni попадания в
	каждый з трех первых и трех последних интервалов малы (меньше
			образом
	5), объед няем				х соответственно в первый и последний. Вычисление
	2	пр ведено в та л. 2.21. Элементы 4-го столбца определяем по
	в
							i
	дующ м				:	А
						А
							190 240,5								240,5
	p1 P( X 190) Ф												Ф
	p1 P( X 190) Ф								19,8				Ф					19,8
									19,8									19,8
	Ф 2.55 Ф 0,4947 0,5 0,0053,
								200 240,5							200 240,5

	p2	P(190 X 200) Ф										Д
									19,8									19,8
	Ф 2.04 Ф 2.55 0,4793 0,4947														0.0154,
										290 240,5						280 240,5
	p11	P(280 X			290) Ф				19,8				Ф						19,8
									19,8										19,8
	Ф 2.5 Ф 1.99 0,4938 0,4767											0,0171.
							240,5							290 240,5
	p12	P(290 X			) Ф							Ф
	p12	P(290 X			) Ф				19,8			Ф			19,8
									19,8						19,8
	Ф Ф 2,5 0,5 0,4938 0,0062.
		Найдем меру расхождения между теоретическим распределени-
	ем и эмпирическим распределением по формулеИ
											2	n	n		np			2	.
														i			i
															npi
												i 1			npi

Вычисления сведем в табл. 2.21. Сложив элементы 8-го столбца, получим

181


2		0,2209		0,2116				1,2321			3,88			0,4356			9,06		5,56
																		19,64
0,53					1,54		4,11			8,97			14,66			18,99
	0,0441		2,37			6,15			0,3741			0,2704			4,5.
			9,54
15,21					4,48		1,71			0,48
С

огласно теореме Пирсона при n распределение величины

2 зависит от параметра k , который называют числом степеней свободы. k = l – 1 – r, где r – число параметров предполагаемого распре-

деления, оцененных по данным выборки, l – число интервалов. Число чение

степеней свободы k 8 1 2 5. Выберем уровень значимости

0,05 по табл це квантилей 2– распределения для числа степеней свободы k 5 уровня значимости 0,05 (см. прил. 4) най-

дем кр т ческое значение кр.2(0,05;5) 11,1; так как наблюденное зна-

оказалось меньше та личного значения, то можно сделать вывод: выдв нутая г потеза о нормальном законе распределения не противореч т опытным данным. Следовательно, гипотезу о нормаль-

ном распределен

генеральной совокупности принимаем.

Индивидуальные задания

1. Измерения скорости света с, произведенные Майкельсоном,

Пизом и Пирсоном, дали результаты, приведенные в табл. 2.22. Для

сокращениябАзаписи в таблице приведены значения (ci – 299 000) км/с.

Получены следующие оценки математического ожидания

и средне-

го квадратического отклонения

, вычисленные по опытным дан-

ным:

=299 733,85 км/с,

=14,7 км/с.

Проверить, используя критерий χ2, согласие опытных данных с

полученным законом распределения при уровне значимости α = 0,05.

Таблица 2.22

Границы

интервала

735

; 740

755

; 760

775 ; 780

795 ; 800

740

; 745

760

; 765

780 ; 785

800 ; 805

745

; 750

765

;770

785 ; 790

805 ; 810

750

;755

770

; 775

790 ; 795

810 ; 815

2. Произведен выбор 200 деталей из текущей продукции прецизионного токарного автомата. Проверяемый размер деталей измерен с

182

точностью до 1 мк. В табл. 2.23 приведены отклонения хi от номинального размера, разбитые на разряды, численности разрядов ni.

Таблица 2.23

	Номер	Границы			Номер	Границы
С		интервала		ni	разряда i	интервала	ni
	разряда i	интервала		ni	разряда i	интервала	ni
		xi ÷ xi+1				xi ÷ xi+1
	1	-20 ; -15		7	6	5 ; 10	41
2		-15 ; -10		11	7	10 ; 15	26
3		-10 ; -5		15	8	15 ; 20	17
измерен				24	9	20 ;25	7
4		-5 ;	0	24	9	20 ;25	7
5		0 ;	5	49	10	25 ; 30	3

Провер ть с помощью критерия соответствия Пирсона гипотезу о

	работанных
нормальном распределении отклонений i от номинального размера.
3.	Имеется 60 деталей, о				на одном станке. Данные
об	ях характерного размера приведены в табл. 2.24.
Провер ть с помощью критерия соответствия Пирсона гипотезу
о нормальном распределении размера х детали.
		А
					Таблица 2.24
	Номер	Размер х,	Номер	Размер х,	Номер	Размер х,
	детали	см	детали	см	детали	см
	1	72,58	21	72,50	41	72,30
	2	72,35	22	72,69	42	72,28
	3	72,33	23	72,54	43	72,51
	4	72,54	24	72,48	44	73,37
	5	72,24	25	72,36	45	72,14
	6	72,42	26	72,50	46	72,42
	7	72,58	27	72,43	И
	7	72,58	27	72,43	47	72,39
	8	72,47	28	Д72,46 48 72,28
	9	72,54	29	72,56	49	72,20
	10	72,24	30	72,48	50	72,4$
	11	72,38	31	72,43	51	72,66
	12	72,70	32	72,56	52	72,64
	13	72,47	33	72,34	53	72,73
	14	72,49	34	72,38	54	72,43
	15	72,28	35	72,56	55	72,28
	16	72,47	36	72,32	56	72,64
	17	71,95	37	72,41	57	72,72
	18	72,18	38	72,14	58	72,34
	19	72,66	39	72,89	59	72,60
	20	72,35	40	72,81	60	72,46

183

4. В табл. 2.25 приведены отклонения диаметров валиков, обработанных на станке, от заданного размера.

Таблица 2.25

0 ; 5

5 ; 10

10 ; 15

15 ; 20

20 ; 25

Границы интервала,

мк

Численность разряда

100

распределении

Провер ть с помощью критерия соответствия Пирсона гипотезу о

нормальном

полученных отклонений.

5. Образовано 250 чисел х, каждое из которых представляет со-

бА

бой сумму ц фр пяти случайных однозначных чисел. Полученные

суммы разб ты на 15

нтервалов в соответствии с табл. 2.26.

Таблица 2.26

Границы

интервала

0 ; 3

15 ; 18

30 ; 33

3 ; 6

18 ; 21

33 ; 36

6 ; 9

21 ; 24

36 ; 39

9 ; 12

24 ; 27

39 ; 42

12 ; 15

27 ; 30

42 ; 45

Суммы, кратные трем, условно отнесены к обоим граничащим интервалам, к каждому из которых отнесена половина числа этих сумм.

Установить, используя критерий χ2, согласуетсяИли приведенное статистическое распределение с законом нормального распределения, за параметры которого приняты оценки математического ожидания и дисперсии, определенные по наблюденным данным, при уровне значимости α =0,05.

6. Результаты наблюдения за среднесуточной температурой воздуха в течение 320 суток приведены в табл. 2.27.

184

		Таблица 2.27

xi°С	ni	xi°С	ni
-40 ÷ 30	5	10 ÷ 20	81
-30 ÷ 20	11	20 ÷ 30	36
-20 ÷ -10	25	30 ÷ 40	20
-10 ÷ 0	42	40 ÷ 50	8
0 ÷ 10	88	50 ÷ 60	4

С
	Провер ть с помощью критерия соответствия Пирсона гипотезу
измерен						Таблица 2.28
о нормальном распределении данных наблюдений при уровне значи-
мости α =0,05.
	7. Имеется 60 деталей, о ра отанных на одном станке. Данные
об		ях характерного размера х приведены в табл. 2.28.
		б
	Провер ть с помощью критерия соответствия Пирсона гипотезу
о нормальном распределении размера х детали.
		Номер	Размер х,	Номер де-	Размер	Номер де-	Размер х,
		детали	см	тали	х,	тали	см
					см
		1	72,50	21	72,35	41	72,31
		2	72,35	22	72,16	42	72,46
		3	72,69	23	72,51	43	72,36
		4	72,60	24	Д
		4	72,60	24	72,50	44	72,39
		5	72,54	А25 72,50 45			72,30
		6	72,42	26	72,48	46	72,30
		7	72,68	27	72,53	47	72,38
		8	72,54	28	72,25	48	72,55
		9	72,55	29	72,48	49	72,36
		10	72,33	30	72,36	50	72,24
		11	72,56	31	72,53	51	72,23
		12	72,86	32	72,23	52	72,16
		13	72,36	33	72,55	53	72,17
		14	72,15	34	72,51	54	72,37
		15	72,48	35	72,25	55	72,38
		16	72,46	36	72,11	И56 72,46
		17	72,36	37	72,44	57	72,12
		18	72,38	38	72,51	58	72,28
		19	72,40	39	72,55	59	72,23
		20	72,38	40	72,24	60	72,38

8. Проверяется партия небольших внешне одинаковых электри-

185

ческих предохранителей для определения тока, при котором происходит их перегорание. Полученные результаты представлены в табл. 2.29.

Проверить с помощью критерия соответствия Пирсона гипотезу о нормальном распределении тока, вызывающего перегорание предохранителей.

Таблица 2.29

	Ток, вызывающ й					92		93	94	95			96	97	98			99			100	101
	перегоран е предо-
	Число
	хран теля, мА
С
		предохран -				3		44	9	10			13	10	8			8			2	2
		телей				3		44	9	10			13	10	8			8			2	2
9.				бА
9.			По данным каталога Воронцова-Вельяминова, распределение
	расстоян й до планетарных туманностей представлено в табл. 2.30,
	где хi – расстоян е (в к							лопарсеках) до туманности, a ni – число слу-
	чаев (ч		сленность разряда).														Таблица 2.30
			xi		ni			xi	ni			xi		ni			xi				ni
		0	; 0,5		9		3,0 ; 3,5		12		6,0 ; 6,5			3		9,0 ; 9,5				2
		0,5 ; 1,0			11		3,5 ; 4,0		7		Д									0
		0,5 ; 1,0			11		3,5 ; 4,0		7		6,5 ; 7,0			2	9.5; 10,0					0
		1,0 ; 1,5			8		4,0 ; 4,5		10		7,0 ; 7,5			1	10,0 ; 10,5					0
		1,5 ; 2,0			12		4,5 ; 5,0		8		7,5 ; 8,0			0
		2,0 ; 2,5			13		5,0 ; 5,5		5		8,0 ; 8,5			0
		2,5 ; 3,0			16		5,5 ; 6,0		0		8,5 ; 9,0			0			21
														И
																n	ni		119
																		i 1

Проверить с помощью критерия соответствия Пирсона гипотезу о нормальном распределении данных наблюдений при уровне значи-

мости α = 0,05.

10. В табл. 2.31 приведены результаты измерения некоторой величины X.

186

																					Таблица 2.31

		Границы ин-					mn			Границы интер-								Границы ин-
		тервала xi							i		вала xi				ni				тервала xi				ni

		75 ÷ 77						2			85 ÷ 87				32				95 ÷ 97				8
С								4			87 ÷ 89				24				97 ÷ 99				3
77 ÷ 79								4			87 ÷ 89				24				97 ÷ 99				3
79 ÷ 81								12			89 ÷ 91				23				99 ÷ 101				1
81 ÷ 83								24			91 ÷ 93				22
83 ÷ 85								25			93 ÷ 95				20				13			200
	значимости																		n ni			200
	значимости																			i 1
																				i 1

		Провер ть,				спользуя критерий χ2, согласие опытных данных с
	законом нормального распределения, параметры которого следует
		бор
	определ ть		основании результатов измерений. Принять уровень
		α =0,05.
		11. Пр			для сортировки электронно-лучевых трубок прове-
	ряется путем многократного пропускания через нeгo одной и той же
									А
	трубки, полученные результаты приведены в табл. 2.32.																						Таблица 2.32
	Отсчет, см			28,8						31,3				33,8					36,3			38,8		41,3
	Число отсче-					2					6			22					38			57		44
		тов											Д
		тов
	Отсчет, см			43,8						46,3				48,8					51,3			53,8			–
	Число отсче-			19							10			0					0			2			–
		тов
		Проверить с помощью критерия соответствия Пирсона гипотезу
																		И
	о нормальном распределении полученных отсчетов при уровне зна-
	чимости α = 0,05.
		12. В табл. 2.33 даны результаты 228 измерений чувствительно-
	сти Х телевизора (в микровольтах).															Таблица 2.33
																Таблица 2.33
								xk		nk		xk		nk				xk		nk
						200				1		450		33			700			13
						250				2		500		34			750			8
						300				11		550		31			800			3
						350				20		600		25				–		–
						400				28		650		19				–		–

187

Проверить, используя критерий χ2, согласование результатов измерения с законом нормального распределения. Принять уровень значимости α =0,05.

13. В табл. 2.34 приведена сгруппированная выборка значений

случайной величины Х объема п = 300.
С					Таблица 2.34
					Таблица 2.34

	Границы	ni	Границы	ni	Границы	ni
	нтервала		интерва-		интерва-
			ла		ла
и				56	150 ; 160	16
50 ; 60		1	100 ; 110	56	150 ; 160	16
60 ; 70		2	110 ; 120	61	160 ; 170	4
70 ; 80		9	120 ; 130	49	170 ; 180	2
80 ; 90		23	130 ; 140	25	–	–
90 ; 100		33	140 ; 150	19	–	–

Провер ть, спользуя критерий χ2 при уровне значимости α = 0,05, соглас е опытных данных с законом нормального распределения.

14. Измерен я скорости света с, произведенные Майкельсоном, Пизом и Пирсоном, дали результаты, приведенные в табл. 2.35. Для сокращения записи в та лице приведены значения (ci – 299 000), км/с.

Таблица 2.35


Границы	ni	Границы	ni	Д			ni
Границы	ni	Границы	ni	Границы	ni	Границы	ni
интервала		бАинтервала интервала				интервала
735 ; 740	3	755 ; 760	17	775 ; 780	40	795 ; 800	5
740 ; 745	7	760 ; 765	23	780 ; 785	17	800 ; 805	2
745 ; 750	4	765 ; 770	29	785 ; 790	16	805 ; 810	3
750 ; 755	8	770 ; 775	45	790 ; 795	10	810 ; 815	4

Проверить, используя критерий χ2, согласие опытных данных с законом нормального распределения при уровне значимости α = 0,05.

15. В табл. 2.36 приведены наблюденные на опыте сроки устра-
нения отказов электронной аппаратуры в часах с точностью до 1 ми-
нуты.	И

Проверить, используя критерий χ2, согласие наблюденных данных с законом логарифмически нормального распределения, при котором x=lgy подчиняется закону нормального распределения, приняв за уровень значимости α = 0,05.

188

																				Таблица 2.36

		Номер			Границы			Численность						Номер		Границы				Численность
	интерва-				интервала			разряда						интерва-		интервала				разряда ni
		ла			yi ; yi+1				ni					ла i		yi ; yi+1
		i
С							3/60		2					8		1,8 ;	3,2			10
1				1/60 ;			3/60		2					8		1,8 ;	3,2			10
2				3/60 ;			6/60		5					9		3,2 ;	5,6			7
3				6/60 ;		10/60			7					10		5,6 ;	10			4
4				10/60 ; 18/60					11					11		10 ;	18			2
5				18/60 ;			35/60		15					12		18 ;	30			1
цизионногоПровер ть с помощью критерия														соответствия Пирсона гипотезу
6				35/60 ;			1,04		21					13		более 30			0
7				1,04 ;			1,8		15
		16. Про зведен вы ор 300 деталей из текущей продукции пре-
					токарного автомата. Проверяемый размер деталей изме-
					бА3 0 ÷ 10 80 7 40 ÷ 50														8
рен с точностью до 1 мк. В та л. 2.37 приведены отклонения хi от но-
минального размера, раз итые на разряды, численности разрядов ni.
о нормальном распределении размера х детали.
																Таблица 2.37
				Номер			Границы						Номер		Границы
			разряда i				интервала			ni		разряда i			интервала					ni
							xi ; xi+1									xi ÷ xi+1
				1			-20 ÷ -10			20		5			20 ÷ 30				40
				2			-10 ÷	0		47		6			30 ÷ 40				16
				4			10 ÷	20		89				–
				4			10 ÷	20		89				–	7
																n ni 300
																i 1
															И
		17. Взяли 120 деталей, обработанных на одном станке, и рас-
смотрели у них отклонения характерногоДразмера от заданного. Про-
веряемый размер деталей измерен с точностью до 1 мк. В табл. 2.38
приведены отклонения хi от номинального размера, разбитые на раз-
ряды, численности разрядов ni.																		Таблица 2.38
																		Таблица 2.38

		Номер			Границы интервала							Номер			Границы интервала
		разряда i			xi ÷ xi+1				ni		разряда i					xi ÷ xi+1					ni
		1			-20 ÷ -15				8		5				0 ÷ 5						35
		2			-15 ÷ -10				16		6				5 ÷ 10						6
		3			-10 ÷ -5				7		7				10 ÷ 15						5
		4			-5 ÷ 0				15		8				15 ÷ 20						8

189

Проверить с помощью критерия соответствия Пирсона гипотезу о нормальном распределении размера х детали.

18. Результаты испытания крепости в граммах нитей приведены далее. При первоначальной группировке длину интервала выбрать равной 20 г.

325 341 285 302 275 284 281 295 220 303 330 286 248 288 261 304 337

305 318 270 285 317 247 301 277 281 247 347 263 280 333 359 325 318

280 271 318 324 287 272 307 286 278 337 348 305 265 287 328 317 282
распределении
255 308 275 285 319 270 301 317 325 305 333 268 319 274 339 324 355
С299 293 291 350 307 290 308 259 315 273 308 330 315 273 310 331 293
272 292 321 291 297 380 312 325 296 263 305 328 307 295 271
		бА
Провер ть			помощью критерия соответствия Пирсона гипотезу
о нормальном					крепости х нитей.
19. Имеется 50 пружин, изготовленных в одинаковых условиях.
Данные об змерен ях жесткости пружин х приведены в табл. 2.39.
Проверить с помощью критерия соответствия Пирсона гипотезу о
нормальном распределении жесткости пружин.
							Таблица 2.39

		Номер	Жест-	Номер		Жест-	Номер	Жест-
	пружи-		кость х,	пружи-		Д
	пружи-		кость х,	пружи-		кость х,	пружи-	кость х,
	ны		кН/м	ны		кН/м	ны	кН/м
	1		32,140	18		32,203	35	32,231
	2		32,152	19		32,207	36	32,244
	3		32,163	20		32,212	37	32,247
	4		32,173	21		32,173	38	32,250
	5		32,169	22		32,216	И
	5		32,169	22		32,216	39	32,240
	6		32,178	23		32,231	40	32,264
	7		32,212	24		32,236	41	32,231
	8		32,216	25		32,212	42	32,236
	9		32,189	26		32,240	43	32,271
	10		32,192	27		32,252	44	32,240
	11		32,198	28		32,255	45	32,264
	12		32,199	29		32,236	46	32,274
	13		32,203	30		32,260	47	32,278
	14		32,195	31		32,264	48	32,293
	15		32,220	32		32,293	49	32,302
	16		32,223	33		32,278	50	32,330
	17		32,226	34		32,286	–	–

190

20. Ниже приведены данные обследования 100 предприятий области по росту выработки на одного рабочего (в % к предыдущему году). Длину интервала взять 10%.

80 100 91 102 103 115 122 118 119 120 104 82 107 111 102 112 115 116

114 115 106 92 109 117 99 98 118 108 107 112 108 102 108 101 103 105

101 106 106 115 109 106 104 107 106 114 116 119 114 123 101 108 105

107 91 104 102 94 103 130 105 109 106 93 105 102 106 108 96 109 108

102 101 95 102 101 100 107 98 108 109 103 111 96 103 104 105 95 99 104 107 104 100 91 115 106 116 101 102 103 2.20.

	Провер ть с помощью критерия соответствия Пирсона гипотезу
С					роста выработки х.
	о нормальном				роста выработки х.
	21. Получено следующее распределение 100 рабочих цеха по вы-
	работке в отчетном году (в процентах к предыдущему году).
	распределении							Таблица 2.40
	распределении
	Выработка в от- 94-104			104-114		114-124	124-134	134-144	∑
	четном году (в % к
	предыдущему)
	Количество		о- 6	20		45	24	5	100
	чих	раб
	чих

распределении случайной величины х – выработки рабочих – с помо-

А На уровне значимости α=0,05Дпроверить гипотезу о нормальном

щью критерия χ2 Пирсона.

22. Произведен выбор 100 проволок и проведены испытания их на прочность. Результаты испытаний приведены в табл. 2.41

		И
			Таблица 2.41
Разрывное	Количество	Разрывное	Количество
усилие	проволок ni	усилие	проволок ni
38 ÷ 40	0	48 ÷ 50	26
40 ÷ 42	1	50 ÷ 52	18
42 ÷ 44	5	52 ÷ 54	2
44 ÷ 46	16	54 ÷ 56	3
46 ÷ 48	28	56 ÷ 58	1

Проверить с помощью критерия соответствия Пирсона гипотезу о нормальном распределении разрывного усилия проверенных проволок.

191

23. Из партии резисторов взяли 50 образцов и произвели замер их сопротивлений. Данные об их отклонениях от номинального значения сопротивления 1 кОм приведены в табл. 2.42.

					Таблица 2.42
	Номер	Откло-	Номер	Отклоне-	Номер	Откло-
	резистора	нение хi,	резистора	ние хi,	резистора	нение хi,
		Ом		Ом		Ом
	1	0.5	18	0.5	35	-1,5
	2	-14,1	19	-5,5	36	8,5
	3	1.0	20	2,0	37	12
	4	-3,0	21	4,0	38	13
	5	1.5	22	-1,0	39	12
С6		2,0	23	5,0	40	-17,0
7		-8,0	24	6,0	41	14
8		2,5	25	-10,5	42	17,0
9		5,0	26	7,0	43	19,0
10		4,5	27	7,5	44	-4,0
и11 3,5			28	0,0	45	21
12		-11,5	29	8,5	46	18,0
13		4,0	30	9,5	47	23,5
14		6,5	31	-20,0	48	19,5
15		7,0	32	10,5	49	-9,0
16		-6,5	33	10,0	50	14,5
	17	7,5	34	11	–	–

					Д
Оценить с помощью критерия χ2							гипотезу о нормальном распре-
делении отклоненийбАхi от номинального сопротивления при уровне
значимости α = 0,05.
24. Проверяется партия небольших внешне одинаковых элек-
трических предохранителей для определения тока, при котором про-
									И
исходит их перегорание. Полученные результаты представлены в
табл. 2.43. Проверить с помощью критерия соответствия Пирсона ги-
потезу о нормальном распределении тока, вызывающего перегорание
предохранителей.												Таблица 2.43
												Таблица 2.43

Ток,	вызываю-	92	93	94		95		96	97	98	99		100	101
щий перегорание
предохранителя,
мА
Число	предохра-
нителей		3	44	9		10		13	10	8	8		2	2

192

25. Результаты обследования роста студентов приведены далее. Первоначально длину интервала при группировке взять равной 4 см.

151 168 170 188 158 170 148 162 166 180 176 176 182 162 173 181

164 166 183 172 174 166 154 167 158 166 173 166 162 169 165 178 164

167 176 153 167 173 165 170 174 168 171 162 177 169 153 169 166 175

172 189 163 160 173 185 170 178 171 172 158 162 170 160 175 166 157

167 153 164 174 180 168 173 181 171 155 173 179 165 184 172 170 175

170 162 159 164 172 193 169 173 174 169 171 168 170 168 177 169

Провер ть с помощью критерия соответствия Пирсона гипотезу

о нормальном	роста х студентов.
С
распределении
§8. Кр тер й равенства двух средних значений

Кр тер й χ2 пр меняется в том случае, когда рассматриваются целые ч сла. Кр тер й t Стьюдента позволяет использовать процен-

ты, дробные ч сла	т. п. Этот критерий применяется для проверки
гипотез различного рода, но мы рассмотрим гипотезу, которая нахо-
дит наиболее широкое применение в инженерной практике: «Средние
двух выборок относятся к одной и той же совокупности». Можно
привести следующие примеры применения этой гипотезы:
«10 резисторов	Д
	из коробки	имеют среднее сопротивление,
равное 12,4бАкОм, а 10 резисторов из коробки В имеют среднее сопро-
тивление 11,9 кОм. В обеих коробках находятся резисторы с одинако-

вым номинальным сопротивлением». «Измерение расхода горючего на трассе протяженностью 100 км, производимое через каждый километр пути, показало, что автомобиль А потребляетИв среднем 0,122 л/км, а автомобиль В – 0,128 л/км. Имеется ли различие в расходе горючего между автомобилями А и В?»

Когда проверяется различие между двумя средними в предположении, что неизвестные генеральные дисперсии равны между со-

бой, формула для критерия t имеет вид

tнабл		x1			x2				.	(2.11)

			1
	sсум		1			1

				n			n	2
			1					2

Величина sсум определяется из выражения

193

sсум2	n 1 s2 n		2	1 s2
	1	1			2	.	(2.12)
		n1 n2 2

Таким образом, для того чтобы при заданном уровне значимости
α проверить нулевую гипотезу Н0: a1= a2					о равенстве математических
ожиданий (генеральных средних) двух нормальных совокупностей с
неизвестными, но одинаковыми дисперсиями при конкурирующей

СстепенейЕслисвободы k = п1 +n2 – 2 найти критическую точку tдвуст. кр(α; k). Велич ну довер тельной вероятности Р=1 – α выбирают в пределах

гипотезе Н1: a1≠ a2, надо вычислить наблюдаемое значение критерия по формуле (2.11) по таблице критических точек распределения тьюдента (см. пр л. 3) по заданному уровню значимости α и числу

0,90–0,99.

|t | < tдвуст. кр(α; k) – нет оснований отвергнуть нулевую гипотезу. Если |tна л|> tдвуст. кр(α; k) – нулевую гипотезу отвергают.

Пр мер 1. Из партии етона, замешанной 25 мая, взяты восемь проб подвергнуты спытаниям на сжатие. Получены следующие данные о прочности на сжатие: 305,6; 270,8; 298,0; 218,6; 273,3; 270,8;

229,4 и 265,8 кг/см2. Из партии етона, замешанной 4 июня, взято 17

проб, и посленаблиспытаний получены следующие результаты: 298,0; 263,4; 288,2; 300,7; 327,9; 303,1; 278,2; 296,0; 316,3; 290,7; 318,0;

270,8; 305,6; 320,5; 293,2;А285,5; 316,3 кг/см2. Насколько известно, со-

став бетона и методика испытаний не менялись. Определите, относятся ли эти две группы данных к одной и той же совокупности, т. е. на уровне значимости, например, α = 0,05 проверить гипотезу о равенстве их средних.

Решение. В этом случае применим критерий t. ля упрощения расчетов составим расчетную табл. 66.

										2132,3						2
										2132,3						2
				Для первой выборки х1							Д= 266,7 кг/см , а для второй
				Для первой выборки х1							Д= 266,7 кг/см , а для второй
				5072,4						8
		2			= 298,1 кг/см2. Используя таблицу результатов (2.44), по
	х
	х
			17
формуле (2.11) вычислим сводную дисперсию для обеих выборок.
						2		6275,79 5218,52						И
						sсум						45,97.
									8 17 2
				При вычислении s2				и s2		воспользовались тем фактом, что
							1	1
				s2	8		2			17						2 17 1 .
				s2	x x		2	8 1 , а s2 x					j	x	2	2 17 1 .
			1		i	1				2	j 1		j		2
					i 1						j 1

194

			Откуда s			45,97					7,1 кг/см2.
																			Таблица 2.44

	xi, кг/см2			xi						2		xj, кг/см2			xj			2
	xi, кг/см2			xi				x1		2		xj, кг/см2			xj		x2	2
	305,6			1513,21								298,0			0,16
С				16,81								263,4			1225,00
270,8				16,81								263,4			1225,00
298,0				979,69								288,2			104,04
270,8				2313,61								300,7			5,29
229,4				43,56								327,9			870,25
265,8				16,81								303,1			20,25
		и										278,2			408,04
229,4				1391,29								278,2			408,04
265,8				0,81								296,0			5,76
	–			–								316,3			320,41
	–			–								290,7			52,29
	–		бА												384,16
	–			–								318,0			384,16
	–			–								270,8			761,76
	–			–								305,6			51,84
	–			–								320,5			488,41
	–			–								293,2			27,04
	–			–								285,5			166,41
	–			–								316,3			320,41
8				8								17				17
	xi		2132,3		xi				x1 2 =6275,79			xj	5072,4			xi			x1	2 =5218,52
	i 1			i 1								j 1				j 1
			Это среднее квадратическое отклонение для двух выборок, рас-
	сматриваемых совместно. Заметим, что для майского замеса характе-
	рен значительно больший разброс данных, чем для июньского. Нахо-
	дим t по формуле (2.12):												И
													И
					t						298,4 266,7		31,7	10,5.
					t						298,4 266,7			10,5.
							набл				7,1 1 8Д117 3,03

Число степеней свободы равно (n1 + n2 - 2) = (8+17-2) = 23. Теперь с помощью таблицы прил. 3 находим, что tдвуст. кр(0,05;23) = 2,07. Так как |tнабл| > tдвуст. кр , нулевую гипотезу о равенстве двух средних отвергаем. Другими словами, справедливость гипотезы, согласно которой обе партии бетона и методика исследований одинаковы, весьма сомнительна.

Пример 2. Рассмотрим эксперимент для оценки четырёх различных приборов для измерения скоростей вращения вала двигателя: стробоскопического тахометра, небольшого визуального устройства «Визутак», механического счетчика оборотов и ручного тахометра.

195

Таблица 2.45

							Группа 1
	Измерительные при-				Тахо-	«Визутак»,		Стробоско-		Счет-	Осцил-
		боры			метр,		об/мин	пический		чик,	лограф,
С					об/мин			тахометр,		об/мин	об/мин
					об/мин			тахометр,		об/мин	об/мин
								об/мин
		1		2			3	4		5		6
				1080			1094	1070		1094	1092
				1073			1080	1069		1088	1089
	ист						1078	1070		1083	1092
	корость вращен я			1079			1078	1070		1083	1092
		вала дв гателя		1079			1075	1070		1088	1086
				1078			1075	1070		1082	1086
		реднее значен е		1078			1080	1070		1087	1089
			бА							2		–
	Отклонен е среднего			11			9	19		2		–
	от	нного значе-
		н я
		Размах		7			19	1		14		6
							Группа 2
		1			2		3	4		5		6
					909		910	905		916		902
					909		900	902		910		914
	Скорость вращения				909		908	901		914		914
		вала двигателя			910		898	902		916		916
					909		902	901		908		916

		Среднее значение			909		904	902		913		912
	Отклонение среднего				3		8	10		-1		–
	от истинного значе-								И
		ния							И
		ния						Д
		Размах			1		12	4 8				14
							Группа 3
					848		810	840		856		855
					847		820	840		848		855
	Скорость вращения				848		820	840		849		855
		вала двигателя			852		820	840		844		855
					844		817	841		850		855
		Среднее значение			849		817	840		850		855
	Отклонение среднего				6		38	15		5		–
	от истинного значе-
		ния

196

Окончание табл.2.45

	Размах		4	10		1	12	0
			729	735		728	736	734
			728	735		727	730	734
	корость вращения		728	725		725	728	734
	вала двигателя		729	720		725	728	734
			729	724		724	726	734
	реднее значение		729	728		726	730	734
	Отклонен е среднего		5	6		8	4	–
	от ист нного значен я
	Размах		1	15		4	8	0
	Испытан я проводятся следующим образом. Устанавливается
С
	перестраивается
	определенная скорость вращения вала, и на экране осциллографа по-
	лучают определенную картину фигур Лиссажу. После этого с четырех
	боров
	различных пр	сн маются данные о скорости вращения об/мин.
	Если карт на на экране осциллографа медленно перемещается, то ге-
	нератор с гналов				и для каждого из четырех приборов

провод тся вторая сер я измерений. При каждой заданной скорости вращен я сн мается пять отсчетов в произвольном порядке чередования скоростей. Лучший план эксперимента состоит в том, что при определенной скорости вращения снимают показания для всего ком-

плекта приборов, затем											ерут другую скорость, а потом снова воз-
вращаются к первоначальной скорости.
В результате описанного выше эксперимента получены данные
о скорости вращенияАвала, которые представлены в табл. 2.45.
																	Таблица 2.46
Тахометр	x										2	7	-1	-1	0	5		2
Тахометр	x						x				2	7	-1	-1	0	5		2
			i					1
			i					1								х1 xi
	x								2		4	49	1	1	0
									2
				x												i 1		=55
		i						1								i 1		=55
«Визутак»											14	0						2
																		2
	xi			x2									Д-2 -5 -5
	xi			x2												5
	x									2	196	0	4	25	25	х2		xi
	x	i			x			2		2	196	0	4	25	25	х2		xi
		i						2								i 1		=250
Стробоскопи-	x										0	-1	0	0	0	5		2
Стробоскопи-	x		i			x					0	-1	0	0	0	5		2
								3
ческий тахо-								3								х3 xi
	x								2		0	1	0	0	0
									2
метр				x												i 1		=1
метр		i						3										=1
														И
																		2
Счетчик	xi			x4							7	1	-4	1	-5	5		2
Счетчик	xi			x4							7	1	-4	1	-5	5
																х4 xi
	x									2	49	1	16	1	25
	x	i			x			4		2	49	1	16	1	25
		i						4								i 1		=92
Осциллограф	x										3	0	3	-3	-3	5		2
Осциллограф	x		i			x					3	0	3	-3	-3	5		2
								5
								5								х5 xi
	x								2		9	0	9	9	9
				x					2
		i		x				5								i 1		=36
		i						5								i 1		=36

197

Проведем анализ полученных статистических данных с целью проверки соответствия показаний осциллографа и остальных четырех приборов. В этом случае применим критерий Стьюдента t. Для первой группы данных результаты вычислений сведем в табл. 2.46.

помощью этих данных вычислим критерий χ2 для каждого из приборов и сравним полученные данные с показаниями осциллографа. Рассматр вая вначале показания тахометра, проверим следующую нулевую г потезу: «Показания тахометра и осциллографа имеют одно то же выборочное среднее» при конкурирующей гипотезе: «Показа-

ния тахометра

осц ллографа имеют различные выборочные сред-

». Используя та л цу результатов и формулу (2.11), вычислим

сводную д сперс ю для о еих вы орок:

Sсум2

n 1 s2 n

1 s2

55 36

11,56

n2 2

ние

При выч слен

s2 и s2 воспользовались тем фактом, что

x x 2

5 1 , а s2

x 2

5 1 .

j 1

i 1

Откуда Sсум 3,4.

По формуле (2.12) вычислим критерий t:

tнабл

1089

1078

5,1.

3,4

0,4

3,4

1 5 1 5

бА

Число степеней свободы равно (n1

- 2) = (5 + 5 -2) = 8. Те-

перь с помощью таблицы прил. 3 находим, что если гипотеза спра-

ведлива, то вероятность появления этого или большего значения t со-

ставляет около 0,001 (tдвуст. кр(0,001;8) = 5,4).

ля уровня значимости α

= 0,05 – tдвуст. кр(0,05;8) = 2,31. ТакДкак |tнабл| > tдвуст. кр – нулевую гипо-

тезу о равенстве двух средних отвергаем. Таким образом, следует от-

клонить данную гипотезу и считать средние значения показаний та-

хометра и осциллографа различными, хотя разница между ними со-

ставляет всего 11 об/мин.

Другими словами, если каждое показание

будет сниматься 100 или даже 1000 раз, все равно следует ожидать

различия в средних.

Такие же вычисления можно выполнить для каждого из осталь-

ных приборов и для остальных трех групп данных. Полученные вероятности сведены в табл. 2.47. Каждое значение Р связано с проверкой гипотезы, согласно которой данный прибор при данной скорости

198

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1914 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20212.9 Mб212072.pdf
#
07.01.20212.9 Mб362073.pdf
#
07.01.20212.9 Mб232074.pdf
#
07.01.20212.91 Mб542075.pdf
#
07.01.20212.92 Mб132076.pdf
#
07.01.20212.92 Mб602078.pdf
#
07.01.20212.93 Mб232079.pdf
#
07.01.2021348.55 Кб17208.pdf
#
07.01.20212.95 Mб422080.pdf
#
07.01.20212.95 Mб22081.pdf
#
07.01.20212.96 Mб142082.pdf