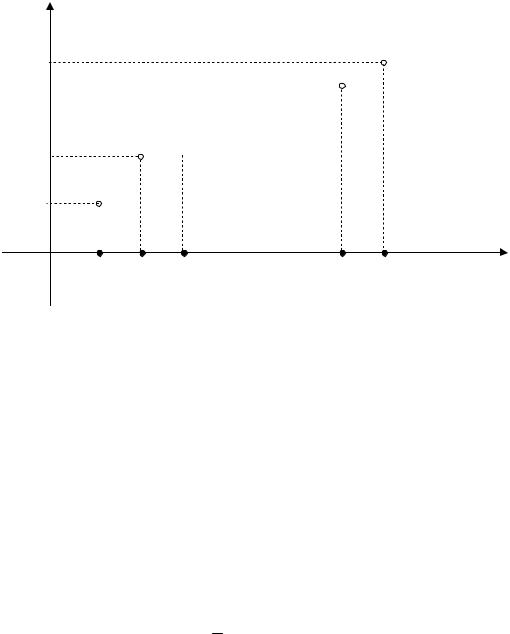
n – объем выборки. Из определения эмпирической функции распределения видно, что ее свойства совпадают со свойствами F(x), а именно:

Можно доказать, что при достаточно большом объеме выборки и при достаточно мелком делении интервалов с практической достоверностью близка к истинной функции распределенияИF (x).

§ 4. Числовые характеристики статистического распределения: выборочное среднее, дисперсия

Параметры распределения

Одна из задач математической статистики: по имеющейся выборке оценить значения числовых характеристик исследуемой случайной величины. Основными числовыми характеристиками выборки являются выборочное среднее хв и выборочная дисперсияDв .

Определение. Выборочным средним называется среднее ариф-

146

метическое значений случайной величины, принимаемых в выборке:

борочное среднеебА, вы орочную дисперсию и т.д.), нужно убедиться, что они в достаточной степени служат приближением соответствующих характеристик генеральной совокупности. Определим требования, которые должны при этом выполняться.

Получив статистические оценки параметров распределения (вы-

1. Если математическое ожидание Ине равно оцениваемому параметру, мы будем получать при вычислении оценок систематиче-

ские ошибки одного знака (с избытком, если М ( ) 0, и с недос-

татком, если М( ) 0). Следовательно, необходимым условием от-

сутствия систематических ошибок является требование М ( ) 0.

Оценка называется несмещенной, если ее математическое

147

ожидание совпадает с истинным значением параметра :M .

2. Определение. Оценка называется эффективной, если она несмещенная и при этом имеет наименьшую дисперсию (наименьший разброс относительно ) по сравнению с другими несмещенными оценками параметра .

3. Определение. Оценка называется состоятельной, если при неогран ченном увел чении объема выборки сходится по вероят-

n 1

её применение теряет смысл.

Пример 1. Оптический пирометр установлен на светящуюся нить накала, различными операторами было произведено несколько измерений температуры. Получены следующие результаты (табл. 2.4).

148

Интервальные оценки математического ожидания и среднего квадратического отклонения

При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, что приводит к грубым ошибкам. Поэтому в таком случае лучше пользоваться интервальны-

149

ми оценками, то есть указывать интервал, в который с заданной вероятностью попадает истинное значение оцениваемого параметра. Разумеется, чем меньше длина этого интервала, тем точнее оценка параметра.

Поэтому, если для оценки θ* некоторого параметра θ справед- Сливо неравенство | θ* – θ | < δ, число δ > 0 характеризует точность

оценки (чем меньше δ, тем точнее оценка). Но статистические методы позволяют говор ть только о том, что это неравенство выполняется с

некоторой вероятностью.

истинноеОпределен е. Доверительным интервалом называется интервал θ* – δ < θ < θ* + δ, в котором с заданной вероятностью заключено значен е не звестного параметра θ. Величина называется доверительной вероятностью или надежностью. Из определения до-

Если бАизвестно, что исследуемая случайная величина Х распределена по нормальному закону Дс неизвестным средним квадратическим отклонением, то для поиска доверительного интервала для ее

верительной вероятности следует, что

=Р ( θ* – δ < θ < θ* + δ ).

На практ ке о ычно ерут =0,95 или =0,99.

Рассмотр м построение доверительных интервалов для математического ож дан я среднего квадратического отклонения нормально распределенной случайной величины.

1. Доверительный интервал для оценки математического ожи-

дания нормального распределения при неизвестной дисперсии.

математического ожидания а построим новую случайную величину

T xв a 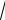n, s

150

Число t к называется критерием Стьюдента для уровня значи-

мости α и числа степеней свободы k = n – 1. Его определяем по табли-

Пример 2. По 25 деталям выборочные характеристики прочности Х составили: хв = 3; s = 1,5. Найти доверительный интервал для математического ожидания нормально распределенной случайной величины Х и точность оценки при = 0,99.

Решение. Из таблицы распределения Стьюдента (см. прил. 3)

находим, что t (n = 25; к=25–1; α = 1– =1–0,99=0,01) = 2,80.

или 2,16< a < 3,84 – доверительный интервал, в который попадает а с вероятностью 0,99. Точность оценки = 0,84.

2. Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения.

Пусть по выборке объёма n получено исправленное среднее

оценкой среднего квадратического отклонения σ случайной величины Х. Будем искать для s нормально распределенной случайной величи-

151

ны доверительный интервал вида s ;s , где s – исправленное выборочное среднее квадратическое отклонение. По определению, доверительный интервал с заданной надежностью Р( |σ – s| < ) = имеет вид s s .

Решение. Точность прибора – это среднее квадратическое отклонение σ случайных ошибок измерений. По условию задачи, n = 20; s =1,3. Найдем доверительный интервал для σ при заданной надежности = 0,95. По прил. 5 находим q (n = 20; = 0,95 ) = 0,37.

с вероятностью 0,95. И

3. Доверительные интервалы для оценки дисперсии.

Считаем, что математическое ожидание неизвестно, а известна

только точечная несмещенная оценка дисперсииs2 . Тогда доверительный интервал для дисперсии, соответствующий доверительной вероятности 1 , имеет вид

152