Белозеров В.И. Учебное пособие по курсу Техническая термодинамика (исправлено)

Åñëè w <<w , òî

12

Как видно из этого уравнения, скорость истечения газа из сопла

w тем больше, чем меньше величина отношений давлений.

2

Расход газа через сопло G вычисляется следующим образом. Объем газа V, вытекающий из сопла в единицу времени, равен

V v2G,

где v – удельный объем в выходном сечении сопла.

2

С другой стороны, величина V может быть определена как

V Sw2 ,

где S – площадь выходного сечения сопла, откуда получаем

G Sw2 .

(12.4.4)

v2

Заменяя в этом соотношении v с помощью уравнения адиабаты,

2

представленного в виде

1

1 §¨ P2 ·¸k 1 , v2 © P1 ¹ v1

получаем

Подставляя сюда значение w из уравнения (12.4.3), имеем

2

161

(12.4.6) на максимум. Величина G достигает максимума тогда, когда достигает максимального значения разность, заключенная в квадратных скобках. Дифференцируя эту разность по \ и приравнивая к нулю, получаем

Чтобы получить из (12.4.3) выражение для скорости истечения газа из сопла при максимальном расходе, нужно подставить в уравнение (12.4.3), найденное по уравнению (12.4.7), значение \ :

Соответственно выражение для величины максимального расхода через сопло получим из (12.4.6) с учетом (12.4.7):

Приступая к расчету истечения идеального газа из сопла при заданных значениях P и P , нужно сначала сравнить отношение

1C

Р /Р с величиной \ , определяемой уравнением (12.4.7). Если

Ñ 1 êð

по уравнениям (12.4.8) и (12.4.9).

163

Расчет скорости истечения реальных газов, как было отмечено ранее, проводится по уравнениям (12.1.7) или (12.1.8) с помощью hS-

диаграмм или P-, v-, T-данных. Площадь выходного сечения сопла подсчитывается по уравнению (12.4.4), которое справедливо для течения любых сред.

12.5. Адиабатное течение с трением

Рассмотрим истечение газа с учетом трения о стенки канала. Процесс течения считаем адиабатным. Вместе с тем очевидно, что

этот процесс необратим – при течении выделяется тепло трения (q )

òð

и энтропия потока увеличивается:

dq

T

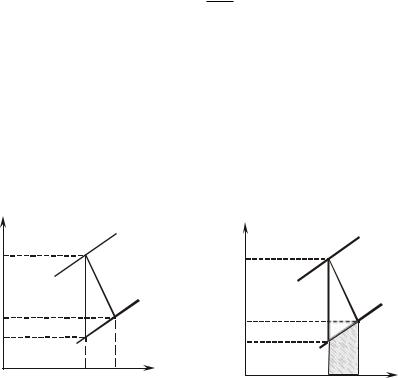
Рассмотрим, как изображается процесс истечения с трением на

hS- и TS-диаграммах (рис. 12.5.1, 12.5.2).

Если бы истечение было обратимым, без трения, то процесс изоб-

ражался бы на hS- и TS-диаграммах отрезком изоэнтропы S = S =

1 2

= const, заключенным между изобарами P и P (между точками 1 и

1 2

2), а скорость на выходе из сопла w определялась бы как (h – h ). Вследствие необратимых потерь при трении энтропия газа в процессе истечения возрастает и действительная адиабата отклоняется от изоэнтропы вправо (рис. 12.5.1). Далее, поскольку расширение газа в потоке с трением и без трения происходит до одного и того же

164

давления на выходе из сопла p , то очевидно, что точка действитель-

2

ного процесса будет лежать на той же изобаре, но правее точки 2

(точка 2д относится к истечению с трением), поскольку S > S .

2ä 2

Поскольку изобары на hS-диаграмме имеют положительный наклон, то

h > h ,

2ä 2

следовательно, и скорость истечения с трением будет меньшей, чем

при течении без трения. Поскольку w < w, то можно записать

ä

ãäå Μ – так называемый скоростной коэффициент, величина которого меньше единицы. Величина Μ лежит в пределах 0,95–0,98.

Потеря энергии потока на преодоление трения (обозначим ее E )

òð

может быть выражена как уменьшение кинетической энергии потока на выходе из сопла при истечении с трением по сравнению с истечением без трения:

Hаконец, из (12.5.5) получаем

165

Приравнивая между собой правые части уравнений (12.5.7) и (12.5.8), имеем

Коэффициенты M и [ для реальных каналов, конечно, не могут быть найдены (определены) термодинамическим путем.

12.6. Общие закономерности течения.

Закон обращения воздействий

Рассмотрим теперь уравнение, описывающее наиболее общий случай течения:

Анализ этого уравнения позволяет сделать интересные заключе- ния о возможных способах ускорения потока.

Значение dP может быть выражено следующим образом:

à

166

С учетом этого соотношения находим из (12.6.1)

Входящий в (12.6.5) дифференциал dv выразим из уравнения не-

T

С учетом (12.6.6)–(12.6.8) получаем из (12.6.5)

Подставляя это соотношение для vdP в исходное уравнение (*) и группируя члены, содержащие dw, в левой части уравнения, получим

167

Проанализируем полученное соотношение. В случае, когда

q= 0, l = 0, dz = 0, уравнение (12.6.11) превращается в уже изве-

âíåø òð

стное нам уравнение

Для случая течения в трубе постоянного сечения (df = 0) при

l= 0, l = 0 и dz = 0, но при наличии подвода (или отвода) тепла к

òåõí òð

потоку получаем из (12.6.11)

водит к ускорению потока (dw > 0), отвод тепла – к его торможению. При подводе тепла газ в потоке расширяется, и его скорость увеличивается. Любопытно отметить, что дозвуковой поток жидко-

§ wv ·

сти, у которой ¨ ¸ < 0 (вода при t < 4°С), будет замедляться при

© wT ¹P

подводе к нему тепла.

Соответственно в сверхзвуковом потоке (М > 1) подвод тепла, как видно из (12.6.12), приводит к торможению потока, а отвод тепла – к

168

ка, к нему нужно подводить тепло. После того, как скорость потока станет звуковой, дальнейшее ускорение потока достигается за счет отвода тепла от сверхзвукового потока.

Тепло к потоку может подводиться (или отводиться) не только через стенки трубы, но и за счет тепла химической реакции, проис-

ходящей в потоке газа.

Рассмотрим процесс течения в негоризонтальной (dz z 0) трубе

Из соотношения следует, что дозвуковой (М < 1) поток газа, движущийся вверх (dz > 0), ускоряется (dw > 0), а сверхзвуковой (М > 1) поток, движущийся вверх, замедляется (dw < 0).

Эти выводы представляют интерес для анализа процессов исте- чения природного газа из скважин (сечение которых постоянно по высоте).

В случае адиабатного потока в трубе постоянного сечения при

dl = 0 и dz = 0, но при наличии потерь энергии на трение получим

òåõí

Из (12.6.14) следует, что при М<1 поток с трением ускоряется (dw > 0) до звуковой скорости, но перейти через скорость звука он не сможет, поскольку для этого нужно было бы отводить тепло от потока, а тепло трения всегда подводится к потоку. Hевозможность в

169

рассматриваемых условиях перехода через скорость звука носит название кризиса течения.

Упомянем еще об одном типе сопла – о так называемом расходном сопле, принцип действия которого состоит в следующем. Если ввести представление о плотности потока в канале как о величи- не расхода газа через единицу площади поперечного сечения канала

f

то из рассмотрения обычного сопла Лаваля следует, что в дозвуковой (сужающейся) части сопла j растет (df < 0 при G = const), достигает максимума в критическом сечении сопла и затем в сверхзвуковой (расширяющейся) части сопла уменьшается (df > 0 при

G= const).

Âтрубе постоянного сечения ( f = const) этого же эффекта можно добиться изменением расхода газа G путем вдувания или отсоса этого газа через отверстия в боковой поверхности трубы (так называемое расходное сопло, рис. 12.6.2).

Если увеличивать расход, вдувая газ, то плотность потока увели- чивается, что эквивалентно сужению геометрического сопла. Если после того, как скорость газа достигнет звуковой, осуществить отвод части газа через боковую поверхность трубы, то j будет уменьшаться и поток будет продолжать ускоряться, ибо это эквивалентно расширению геометрического сопла.

Уравнение (12.6.11), позволяющее установить знак воздействия в зависимости от величины М, носит название закона обращения

воздействий.

170