Глава 1. Линейные уравнения

Линейные уравнения – первые уравнения, с которыми мы встречаемся в школе и пройти мимо которых нам не удастся ни в одном разделе высшей математики.

§ 1.1. Уравнения с одной неизвестной

( 2 − 5 · + 6) = 2 2 − 3 − 2.

Найти решение относительно неизвестной величины .

Решение:

1) Коэффициент при равен нулю, если 2 − 5 + 6 = 0.

Корни квадратного трехчлена: 1 = 2, 2 = 3. 1.1) = 2 0 · = 0. Множество решений – . 1.2) = 3 0 · = 7. Множество решений – .

2) При ( ̸= 2)&( ̸= 3) уравнение имеет единственное решение:

Ответ:

1) при = 2.

2) при = 3.

3) = 2 +1 при ( ̸= 2)&( ̸= 3).

−3

Задачи к параграфу на с. 188, п. 1.

§ 1.2. Уравнения с двумя неизвестными

19 28 Линейное уравнение с двумя неизвестными в общем виде: + = . Поскольку уравнение связывает две неизвестные величины, решениями его будет множество пар ( ; ), которое можно интерпретировать как геометрическое место точек плоскости. Если коэффициенты при ине равны одновременно нулю, такому уравнению соответствует прямая на плоскости. Многим более привычна запись уравнения прямой в виде = + · , где – отрезок, отсекаемый прямой на оси , а – угловой коэффициент прямой, т. е. тангенс угла наклона прямой по отношению к оси .

Такое уравнение также является линейным, но «не в общем виде», поскольку не может задать прямую, параллельную оси . Исследуем уравнение.

1) ( = 0)&( = 0).

1.1) = 0. Уравнение принимает вид 0 · + 0 · = 0. Его решением будет множество всех пар вещественных чисел:

{( ; )}, где , . Иначе множество решений можно записать в виде ( ; ). Это множество всех точек плоскости. 1.2) ̸= 0. Уравнение принимает вид 0 · + 0 · = . Множество решений – .

2) ( ̸= 0)&( = 0). Задача сводится к решению линейного уравнения с одной неизвестной · = . Решением будет множеств пар

Этому множеству соответствует прямая, параллельная оси

и пересекающая ось в точке (рис. 1б).

3) ( = 0)&( ̸= 0). Решением будет множество пар

Этому множеству соответствует прямая, параллельная оси

и пересекающая ось в точке (рис. 1а).

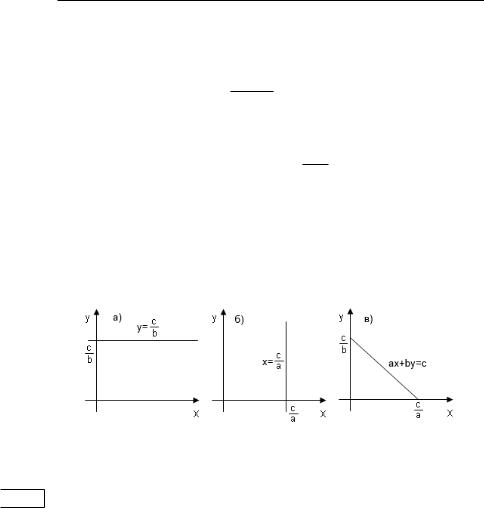
22 ГЛАВА 1. ЛИНЕЙНЫЕ УРАВНЕНИЯ

4) ( ̸= 0)&( ̸= 0). Решение можно записать в виде

{ ( ) }

; − | .

Ему соответствует прямая на плоскости, непараллельная ни одной из координатных осей: = (рис. 1в).

Если коэффициенты уравнения и свободный член являются функциями некоторой переменной, например , то говорят об однопараметрическом семействе линейных уравнений или об однопараметрическом семействе прямых.

Рис. 1. Прямые на плоскости

188 Пример 1. Исследовать уравнение

( 2 + 3 + 2) + ( 2 − 2 − 3) = 2 − 4.

Решение. Здесь мы имеем дело с однопараметрическим семейством линейных уравнений. Разложив соответствующие квадратные трехчлены на множители, получим:

( + 1)( + 2) + ( + 1)( − 3) = ( − 2)( + 2).

1) Коэффициенты при и одновременно равны нулю толь-

ко при = −1. В этом случае уравнение примет вид

0 · + 0 · = −3. Множество решений – .

2) При ̸= −1 можно рассмотреть два случая. 2.1) Если = 3, то 20 = 5 = 14 .

2.2) Если ̸= 3, решение можно записать в виде

Таким образом, если вас попросят указать решения уравнения 2 + 3 = 6, вы смело можете сказать, что это все пары вещественных чисел ( , ), удовлетворяющие отношению 2 + 3 = 6, или записать множество решений в виде

{( , )|2 + 3 = 6; , }.

Пример 2. Леша и Гоша подрядились на работу. Требова- 188

лось напечатать тексты, разложить их по конвертам, подписать и заклеить конверты. Известно, что Леша печатает текст за 5 минут, а работа с конвертом занимает у него всего

1 минуту. Гоше для печатания текста требуется 10 минут, а конверт он оформляет за 5 минут. Очевидно, Леша за час может выполнить 10 единиц работы, а Гоша только 4. Работая отдельно, они в сумме выполнят за час 14 единиц работы, иначе говоря, производительность команды составит 14 единиц продукции в час. Вопрос: можно ли распределить работу так, чтобы общая производительность команды увеличилась? Иногда с ходу предлагают поручить Леше, как самому расторопному, более трудоемкую операцию с текстами, а Гоше оставить работу с конвертами. Но тогда Леша за час напечатает 12 текстов, а Гоша за это время справится с 12 конвертами. Еще хуже! Найдем оптимальное решение.

Решение. Поскольку Леша набирает 5 текстов в час, производительность его труда по текстам равна 12 единиц в час. Это производительность по конкретной производственной операции. Соответственно, его производительность по конвертам – 60 ед./ч. Производительность труда Гоши по текстам – 6, по конвертам – 12 ед./ч. Нам предстоит ответить на вопрос: какую долю времени каждый из них должен тратить на тексты, а какую на конверты? Обозначим долю времени, отведенную работе с текстом, для Леши через , а для Гоши через . Тогда они вместе за час должны набрать

12 + 6 текстов. Доли времени, отведенные на конверты для Леши и Гоши, составят соответственно 1− и 1− , т. е.

все время, свободное от работы с текстами. За это время они оформят 60(1 − ) + 12(1 − ) конвертов. Количество напечатанных текстов должно равняться количеству конвертов:

12 +6 = 60(1− )+12(1− ). Приведя подобные и сократив левую и правую части полученного уравнения на 18, получим 4 + = 4. Распределение времени для Леши и Гоши однозначно определяется парой ( ; ), которую можно считать координатами некоторой точки на плоскости. Чтобы количество текстов совпало с количеством конвертов, эта точка должна лежать на прямой : 4 + = 4 (рис. 2). Кроме того, по смыслу задачи на величины и накладываются ограничения , [0; 1]. Тогда все допустимые пары ( ; )

Рис. 2. Точка соответствует оптимальному плану

должны лежать на отрезке AC. Количество единиц конечно-

го продукта равно количеству текстов: = 12 + 6 . В част-

(прямая 1 на рис. 2). Эта прямая пересекается с отрезком

в точке (1; 0). Если теперь мы начнем увеличивать значение параметра , прямая 12 + 6 = будет смещаться вверх параллельно самой себе. Когда прямая займет положение 2, она пересечет отрезок в точке , соответствующей случаю, когда Леша и Гоша работали по отдельности

= 56 ; = 46 , т. е. когда команда производила 12 + 6 = 14

единиц конечного продукта. Итак, со смещением прямой 1

вверх параллельно самой себе производительность команды растет. К сожалению, двигать прямую вверх без конца мы не можем. Действуют ограничения. Самое верхнее допустимое положение 1 – это 3, когда прямая пересекает отрезок в точке (34 ; 1). В этом случае 12 + 6 = 15.

Ответ: команда достигнет максимальной производительности труда – 15 единиц конечного продукта в час, если Леша три четверти часа будет заниматься текстами и четверть часа конвертами, а Гоша только текстами.

Немного теории. Если функция = ( ) определена и дифференцируема на всей вещественной оси или некотором ее интервале, в любой точке ее области определения существует касательная. Уравнение прямой, касающейся графика функции в точке с координатами ( , ( )), можно представить в виде = ( ) + ′( ) ·( − ). Когда принимает значения из области определения ( ), касательная принимает