Ответ:

(10 −5)2(10 −4)(10 −6)−72 = (100 2−100 +33)(10 −8)(10 −2).

§ 3.3. Неравенства

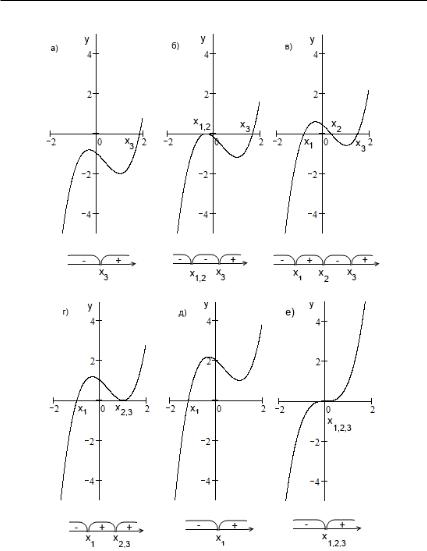
107 132 Рассмотрим многочлен третьей степени с одной неизвестной, графиком которого является кубическая парабола (рис. 21). В общем виде уравнение кубической параболы выглядит так:

3( ) = 3 + 2 + + .

Кубический многочлен имеет один или три вещественных корня, при этом допускаются кратные корни, т. е. совпадающие. Совпадать могут два корня, либо все три, в последнем случае многочлен представляется в виде ( − )3. Функция = 3( ) может иметь один локальный максимум и один локальный минимум, которые находятся из условия равенства нулю производной 3′( ) = 3 2 + 2 + .

126 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА

Рис. 21. Кубическая парабола

Если старший коэффициент > 0,

lim ( ) = −∞ и lim ( ) = +∞.

На рис. 21а изображен график кубической параболы

3( ) = 3 − 2 − − 1. Уравнение 3( ) = 0 имеет един-

ственное решение, соответствующее точке пересечения гра-

фика с осью . Формула Кардано (с. 149) дает значение

√

3 = 98+15 33 . Теперь начнем увеличивать свободный член

9

до тех пор, пока график не коснется оси в точке локального максимума (см. рис. 21б). Это произойдет, когда свободный член достигнет значения = −275 и уравнение примет вид 3 − 2 − − 275 = 0. Теперь многочлен имеет кратный корень 1,2 = −13 , соответствующий точке касания

√

3 = 1+23 3 . Поднимем график еще выше, так, чтобы он касался оси в точке локального минимума (см. рис. 21г). Свободный член = 1, и 3( ) = 3 − 2 − + 1. Многочлен легко раскладывается на множители ( − 1)2( + 1) и

имеет три корня: 1 = −1 и кратный корень 2,3 = 1. Еще раз поднимем кубическую параболу вверх, увеличив на 1

(см. рис. 21д). Многочлен примет вид 3( ) = 3 − 2 − + 2

и теперь имеет один вещественный корень, который можно

128 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА

Уже само аналитическое представление корня объясняет, почему мы не спешим предъявить соответствующую формулу. На рис. 21е также изображена кубическая парабола

3( ) = 3, имеющая корень третьей кратности = 0. Как видно на графиках (см. рис. 21а–21д), если корень имеет единичную кратность, многочлен в соответствующей точке пересекает ось и меняет знак на противоположный. Корни единичной кратности называют простыми. Если встречается корень второй кратности, в этой точке график только касается оси , но многочлен не меняет знак. Многочлен на рис. 21е в точке = 0 имеет корень третьей кратности и в этой точке меняет знак на противоположный. Под каждым графиком помещена схема промежутков знакопостоянства, на основании которой можно сразу записывать ответы к соответствующим неравенствам.

200 Пример 1. Решить неравенство 3( ) > 0 (см. рис. 21а).

Ответ: ( 3; +∞).

200 Пример 2. Решить неравенство 3( ) < 0 (см. рис. 21б).

Ответ: (−∞; 1) ( 1; 3).

200 Пример 3. Решить неравенство 3( ) ≥ 0 (см. рис. 21в).

Ответ: [ 1; 2] [ 3; +∞).

Пример 4. Решить неравенство 3( ) ≤ 0 (см. рис. 21г). 200

Ответ: (−∞; 1] { 2}.

Теперь немного теории. До сих пор мы не определили понятие кратности корня. По теореме на с. 110, если число является корнем многочлена ( ), многочлен делится на

( − ) без остатка. Иначе говоря, ( ) = ( − ) −1( ). Если имеет место равенство

( ) = ( − ) − ( ),

но ( ) не делится без остатка на ( − ) +1, то является k-кратным корнем многочлена. Линейный член ( − )

сохраняет знак при переходе через точку , если – четное число (см. рис. 21б и 21г), и меняет знак на противоположный в противном случае (см. рис. 21е). Одновременно при этом меняется и знак всего многочлена. Примем без доказательства тот факт, что любой многочлен с вещественными коэффициентами раскладывается в произведение линейных членов, соответствующих вещественным корням, и квадратных трехчленов c отрицательным дискриминантом. Теперь можно сформулировать алгоритм решения неравенств с многочленом в левой части:

1) разложить многочлен на степени линейных множителей, соответствующие их кратности, и квадратные трехчлены с отрицательным дискриминантом;

Рис. 22. Промежутки знакопостоянства из примера 5

Решение. Многочлен в левой части неравенства обращается в ноль в точках −3, −2, 1, 2, 3. Отметим их на схеме (рис. 23) жирными точками, поскольку они войдут в решение. Все корни простые, т. е. единичной кратности, а значит, делят вещественную ось на шесть промежутков знакопостоянства. Подставив в многочлен = 0, найдем знак на интервале (−2; 1). На этом интервале будет знак «−». Опять по принципу чередования расставим знаки в остальных интервалах, как показано на рис. 23.

Ответ: (−∞; −3] [−2; 1] [2; 3].

Рис. 23. Промежутки знакопостоянства из примера 6

( 2 + + 1)( − 1)2( − 3)(2 − )( − 4)3 ≤ 0.

Решение. Многочлен в левой части неравенства обращается в ноль в точках 1, 3, 4. Мы отметим их, как решения, жир-