Мы пришли к следующей эквивалентной исходной системе:

17 2 − 58 − 40 2 = 0;

3 2 − 2 = 160.

Разделим первое уравнение на 2 и обозначим = . Найдем

дискриминант уравнения 17 2 − 58 − 40 = 0:

√

= 582 − 4 · 17 · (−40) = 6084 > 0. 6084 = 78. Корни

уравнения: 1,2 = 5834±78 1 = −1017 ; 2 = 4.

1) = −1017 = −1017 10 = −17 . Умножим второе уравнение на 10 и подставим (−17 ) вместо 10 :

64 2 = 1600 = ±5 = 172 .

2) = 4 = 4 . Подставим = 4 во второе уравнение системы: 40 2 = 160 2 = 4 = ±2 = ±8.

§ 2.6. Уравнения с тремя неизвестными

94 102 Уравнения второго порядка с тремя неизвестными в задачах средней школы встречаются нечасто. Общий вид уравнения:

11 2 + 22 2 + 33 2 + 2 12 + 2 13 + 2 23 +

+ 1 + 2 + 3 + 0 = 0.

За исключением вырожденных случаев, каждому такому уравнению соответствует поверхность в трехмерном пространстве. Несмотря на большое количество членов уравнения, соответствующих типов поверхностей не так уж много. Просто существует континиум способов расположения поверхности в системе координат. Как и в случае уравнений второго порядка, в некоторой системе координат запись уравнений имеет канонический вид. Прежде всего заметим, что каждой кривой второго порядка плоскости

в пространстве соответствует цилиндрическая поверхность. Это эллиптический (рис. 19а), гиперболический (рис. 19б) и параболический (рис. 19в) цилиндры. Действительно, каж-

Рис. 19. Цилиндрические поверхности

дой точке плоскости с координатами ( 0; 0) соответствует в пространстве прямая, т. е. множество точек с координатами

( 0; 0; ), где . Если прямую перемещать параллельно самой себе вдоль некоторой плоской кривой, она опишет в пространстве цилиндрическую поверхность. Однако класс

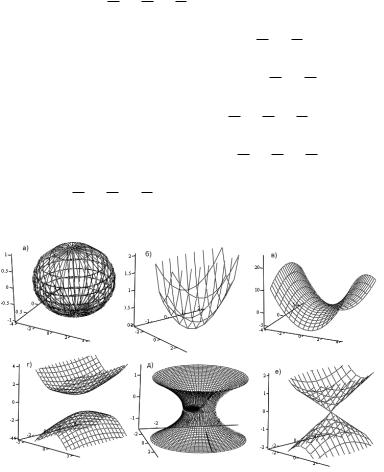
поверхностей второго порядка несколько шире (рис. 20):

1.Эллипсоид: 22 + 22 + 22 = 1 (20а).

2.Эллиптический параболоид: = 22 + 22 (20б).

3.Гиперболический параболоид: = 22 − 22 (20в).

4.Двуполостный гиперболоид: 22 + 22 − 22 = −1 (20г).

5.Однополостный гиперболоид: 22 + 22 − 22 = 1 (20д).

6.Конус: 22 + 22 − 22 = 0 (20е).

Рис. 20. Основные типы поверхностей второго порядка

Cечение любой поверхности второго порядка плоскостью –

кривая второго порядка.