
Ankilov
.pdf

2. Будем искать зависимость в виде
y (x, a,b, c) ax2 bx c.
Для нахождения параметров a, b, c составим нормальную систему
|
|
|
|
|
|
|
n |
|
|
|
n |
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
yi xi2 |
a xi4 |
b xi3 c xi2 0, |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
i 1 |
|
i 1 |
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
yi xi |
a xi3 |
b xi2 c xi 0, |
|
|
|
|
||||||
|
|
|
|
|
|
|
i 1 |
|
|
|
i 1 |
|
i 1 |
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
n |
|
|
|
|
|
||
|
|
|
|
|
|
|
yi a xi2 |
b xi c n 0. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
i 1 |
|
i 1 |
|
i 1 |
|
|
|
|
|
|||
|
|
Определим коэффициенты системы: |
|
|
|
|
|
|
Таблица 7.21 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Определение коэффициентов нормальной системы уравнений |
|
||||||||||||||
|
i |
|
x |
y |
i |
|
x2 |
|
|
|
|
x3 |
|
x |
x y |
i |
x2 y |
i |
|
|
|
|
i |
|
|
|
i |
|
|
|
|
i |
|
i |
i |
i |
|||
|
1 |
|
0,1 |
1,25 |
|
0,01 |
|
|
|
0,001 |
|
0,0001 |
0,125 |
0,0125 |
|||||
|
2 |
|
0,2 |
1,38 |
|
0,04 |
|
|
|
0,008 |
|
0,0016 |
0,276 |
0,0552 |
|||||
|
3 |
|
0,3 |
1,56 |
|
0,09 |
|
|
|
0,027 |
|
0,0081 |
0,468 |
0,1404 |
|||||
|
4 |
|
0,4 |
1,78 |
|
0,16 |
|
|
|
0,064 |
|
0,0256 |
0,712 |
0,2848 |
|||||
|
5 |
|
0,5 |
1,95 |
|
0,25 |
|
|
|
0,125 |
|
0,0625 |
0,975 |
0,4875 |
|||||
|
6 |
|
0,6 |
2,31 |
|
0,36 |
|
|
|
0,216 |
|
0,1296 |
1,386 |
0,8316 |
|||||
|
7 |
|
0,7 |
2,52 |
|
0,49 |
|
|
|
0,343 |
|
0,2401 |
1,764 |
1,2348 |
|||||
|
8 |
|
0,8 |
2,81 |
|
0,64 |
|
|
|
0,512 |
|
0,4096 |
2,248 |
1,7984 |
|||||
|
9 |
|
0,9 |
3,14 |
|
0,81 |
|
|
|
0,729 |
|
0,6561 |
2,826 |
2,5434 |
|||||
|
10 |
|
1,0 |
3,52 |
|
1,00 |
|
|
|
1,000 |
|
1,0000 |
3,520 |
3,5200 |
|||||
|
11 |
|
1,1 |
4,12 |
|
1,21 |
|
|
|
1,331 |
|
1,4641 |
4,532 |
4,9852 |
|||||
|
12 |
|
1,2 |
5,01 |
|
1,44 |
|
|
|
1,728 |
|
2,0736 |
6,012 |
7,2144 |
|||||
|
|
|
7,8 |
31,35 |
|
6,50 |
|
|
|
6,084 |
|
6,071 |
24,844 |
23,1082 |
|||||
|
|
Нормальная система имеет вид |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
a 6,071 b 6,084 c 6,50 |
23,1082, |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24,8440, |
|
|
|
|
|
|
|
|
|
|
|
a 6,084 b 6,500 c 7.80 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 6,500 b 7,800 c 12 31,3500. |
|
|
|
|
||||||||
Решив систему методом Гаусса (см. лабораторную работу №1), получим |
|
|
|
||||||||||||||||
|
|
|
|
|
a 2,401349; |
|
b 0,001673; |
c 1,310682, |
|
|
|
||||||||
следовательно, функция имеет вид |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
y 2,401349x2 |
0,001673x 1,310682. |
|
|
|
|
|||||||
Найдем невязку |
|
|
yi 2,401349xi2 0,001673xi |
1,310682 2 |
|
|
|
|
|||||||||||
|
|
|
|
|
12 |
|
|
|
|
||||||||||
|
|
|
|
|
|
0,395. |
|
|
|||||||||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Построим график функции y(x) и экспериментальные точки (рис. 7.24).
262
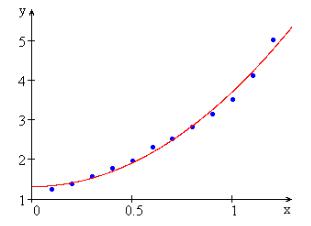
Рис. 7.24.
4. Продолжаем выполнение работы в компьютерном классе. Запускаем программу Mathcad. Открываем файл Lab5.mcd. Вводим таблицу значений:
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
1.1 |
1.2 |
C : |
|
|
|
|
|
|
|
|
|
|
|
|
1.38 |
1.56 |
1.78 |
1.95 |
2.31 |
2.52 |
2.81 |
3.14 |
3.52 |
4.12 |
|
1.25 |
5.01 |
5. Вычисляем коэффициенты аппроксимации многочленами третьего и четвертого порядков. Для этого поочередно вводим в программу k : 3 и k : 4 .
Для первого случая компьютер выведет вектор коэффициентов a0 , a1,..., ak функции
y a |
0 |
a x a |
2 |
x2 |
... a |
k |
xk : |
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
aТ (0.906061 3.128965 |
3.378954 2.964258) , |
||
и выписываем аппроксимирующий многочлен третьего порядка и его невязку
y 0,906061 3,128965 x 3,378954 x2 2,964258 x3 , |
0,233. |
Для второго случая компьютер выведет вектор коэффициентов
aТ (1.334242 1.739054 11.962267 14.876651 6.861888) ,
и выписываем аппроксимирующий многочлен четвертого порядка и его невязку
y 1,334242 1,739054 x 11,962267 x2 14,876651x3 6,861888 x4 , |
0,101. |
6. Далее проводим аппроксимацию эксперимента линейной комбинацией четырех функций x, ex , sin(x),1 . В файле Lab5.mcd запрограммировано нахождение коэффициентов
этой комбинаций, как с помощью решения нормальной системы уравнений, так и с использованием стандартной функции системы Mathcad linfit (см. п. 7.6.2). Для этого вводится векторнозначная функция
|
x |
|
|
ex |
|
F(x) : |
|
. |
sin(x) |
|
|
|
1 |
|
Автоматически получаем вектор коэффициентов комбинации
44.940186
7.813314 V 34.251373
8.790875
и невязку
0,2982 .
Следовательно, аппроксимирующий закон имеет вид
263


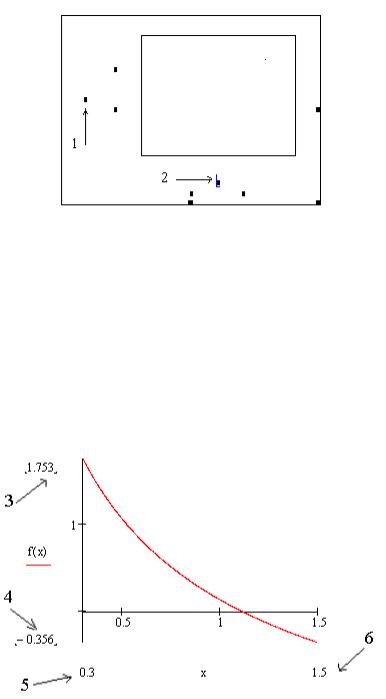
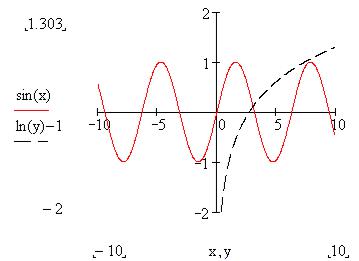
Рис. 7.27.
Если два раза щелкнуть мышью в поле графика, то во всплывающем окне «Formatting Currently Selected X-Y Plot» можно установить параметры отображения осей и линий графика. В первой закладке «X-Y Axes» («Оси X-Y») можно выбрать вид координатных осей, наложить сеть и установить ее размер, откорректировать масштаб. Во второй закладке «Traces» («След») можно установить параметры всех отображаемых линий (trace 1, trace2 и т. д.): наименование, цвет, толщину, тип (непрерывный, пунктир или точками для дискретных функций). В третьей закладке «Labels» («Метки») можно ввести названия графика и координатных осей.
7.6.6. Программные блоки
Для решения многих задач в системе Mathcad используются программные блоки. В начале любого блока обязательно должно присутствовать служебное слово Given, далее идет тело блока и в конце стандартная функция, закрывающая блок. В процессе программирования лабораторных работ были использованы четыре программных блока.
В файле Lab1.mcd, в качестве дополнительной информации, показан способ получения общих решений систем линейных алгебраических уравнений и частных решений нелинейных систем с помощью программного блока «Given – Find». Например,
Given |
|
|
|
|
a 2b 3c 1 |
|
|
|
|
4a 5b 6c 2 |
|
|
|
. |
7a 8b 9c 3 |
|
|
|
|
|
c |
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2c |
|
2 |
|
Find (a,b,c) |
|
|||
|
c |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь телом блока является система уравнений, а с помощью функции Find(x,y,….) получаем искомое решение, где x, y,... есть скалярные переменные, значения которых ищутся в блоке решения уравнений.
В файлах Lab2.mcd и Lab3.mcd для нахождения максимального и минимального значений функции в некоторой области использованы программные блоки «Given –
270
