
99-105
.docx99. Определенный интеграл
Интегральной
суммой функции f(x)
на отрезке [a; b]
называется сумма 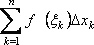 ,где
,где ![]() , причем
, причем![]() .
.
Если
существует не зависящий от способа
разбиения отрезка [a; b]
на частичные отрезки ![]() и
выбора промежуточных точек
и
выбора промежуточных точек ![]() предел
интегральной суммы при
предел
интегральной суммы при ![]() ,
то функция f(x) называется
интегрируемой на этом отрезке, а сам
предел – определенным интегралом от
функцииf(x) на
отрезке [a; b]
и обозначается
,
то функция f(x) называется
интегрируемой на этом отрезке, а сам
предел – определенным интегралом от
функцииf(x) на
отрезке [a; b]
и обозначается  .
Таким образом,
.
Таким образом,
 . (60)
. (60)
Если F(x ) – одна из первообразных непрерывной на [a; b] функции f(x), то справедлива формула Ньютона – Лейбница
 . (61)
. (61)
Если
функции ![]() и
и ![]() непрерывны
вместе со своими производными на [a; b],
то имеет место формула интегрирования
по частям
непрерывны
вместе со своими производными на [a; b],
то имеет место формула интегрирования
по частям
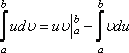 . (62)
. (62)
Если
функция f(x) непрерывна
на [a; b],
а функция ![]() непрерывно
дифференцируема и строго возрастает
на
непрерывно
дифференцируема и строго возрастает
на ![]() ,
, ![]() ,
то справедлива формула
,
то справедлива формула
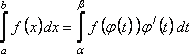 , (63)
, (63)
называемая формулой замены переменной в определенном интеграле.
Приложения
определенного интеграла![]()
Площадь
криволинейной трапеции, ограниченной
графиком функции ![]() ,
прямыми х
= а, х = b и
осью Ох,
вычисляется по формуле
,
прямыми х
= а, х = b и
осью Ох,
вычисляется по формуле
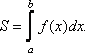 (64)
(64)
Если ![]() ,
то
,
то 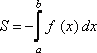 .
.
Пусть ![]() и
и ![]() –
непрерывные на
–
непрерывные на ![]() функции
и
функции
и ![]() при
любом
при
любом ![]() .
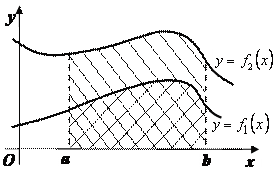
Тогда площадь фигуры, ограниченной
графиками функций
.
Тогда площадь фигуры, ограниченной
графиками функций ![]() ,
вычисляется по формуле
,
вычисляется по формуле
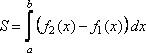 . (65)
. (65)
Действительно,
если функции ![]() ,
то данная формула является очевидным
следствием того, что площадь фигуры
равна разности площадей криволинейных
трапеций (рис. 14)
,
то данная формула является очевидным
следствием того, что площадь фигуры
равна разности площадей криволинейных
трапеций (рис. 14)
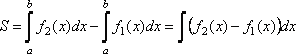 .
.
Если
графики функций ![]() и
и ![]() полностью
или частично расположены ниже оси
полностью
или частично расположены ниже оси ![]() ,
то существует константа
,
то существует константа ![]() ,
такая, что
,
такая, что ![]() и
и ![]() .
.
Сделаем
замену ![]() (рис.
15). Тогда очевидно, что
(рис.
15). Тогда очевидно, что
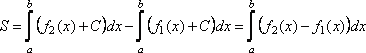 .
.

100. С геометрической точки зрения для неотрицательной функции y = f(x) на отрезке [a; b] точное значение определенного интеграла представляет собой площадь криволинейной трапеции, а приближенное значение по методу прямоугольников – площадь ступенчатой фигуры.

Перейдем
к оценке абсолютной погрешности метода
прямоугольников. Сначала оценим
погрешность на элементарном интервале.
Погрешность метода прямоугольников в
целом будет равна сумме абсолютных
погрешностей на каждом элементарном
интервале.
На каждом отрезке ![]() имеем
приближенное равенство
имеем
приближенное равенство 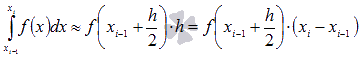 .
Абсолютную погрешность метода
прямоугольников
.
Абсолютную погрешность метода
прямоугольников ![]() на i-ом
отрезке вычисляем как разность между
точным и приближенным значением
определенного интеграла
на i-ом
отрезке вычисляем как разность между
точным и приближенным значением
определенного интеграла  .
Так как
.
Так как 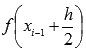 есть
некоторое число и
есть
некоторое число и  ,
то выражение
,
то выражение  в
силу четвертого свойства
определенного интеграла можно
записать как
в
силу четвертого свойства
определенного интеграла можно
записать как  .
Тогда абсолютная погрешность формулы
прямоугольников на i-ом
элементарном отрезке будет иметь
следующий вид
.
Тогда абсолютная погрешность формулы
прямоугольников на i-ом
элементарном отрезке будет иметь
следующий вид
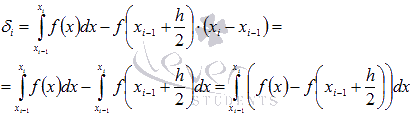 Если
считать, что функция y
= f(x) имеет
в точке
Если
считать, что функция y
= f(x) имеет
в точке ![]() и
некоторой ее окрестности производные
до второго порядка включительно, то
функцию y
= f(x) можно
разложить в ряд
Тейлора по
степеням
и
некоторой ее окрестности производные
до второго порядка включительно, то
функцию y
= f(x) можно
разложить в ряд
Тейлора по
степеням 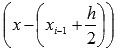 с
остаточным членом в форме Лагранжа:
с
остаточным членом в форме Лагранжа:
 По
свойствам определенного интеграла
равенства можно интегрировать
почленно:
По
свойствам определенного интеграла
равенства можно интегрировать
почленно:
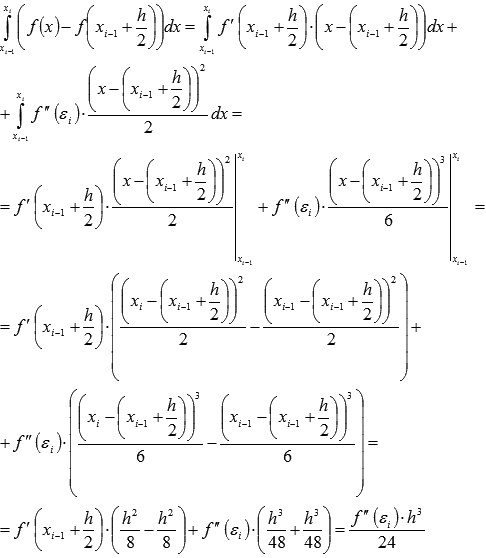 где
где ![]() .
Таким
образом,
.
Таким
образом, 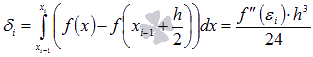 и
и  .
Абсолютная
погрешность формулы прямоугольников
на отрезке [a;
b] равна
сумме погрешностей на каждом элементарном
интервале, поэтому
.
Абсолютная
погрешность формулы прямоугольников
на отрезке [a;
b] равна
сумме погрешностей на каждом элементарном
интервале, поэтому
 и
и 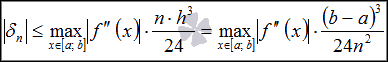 .
Полученное
неравенство представляет собой оценку
абсолютной погрешности метода
прямоугольников.
Перейдем
к модификациям метода прямоугольников.
.
Полученное
неравенство представляет собой оценку
абсолютной погрешности метода
прямоугольников.
Перейдем
к модификациям метода прямоугольников.
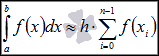 -
это формула
метода левых прямоугольников.
-
это формула
метода левых прямоугольников.
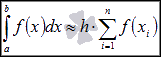 -
это формула
метода правых прямоугольников.
-
это формула
метода правых прямоугольников.

Отличие
от метода средних прямоугольников
заключается в выборе точек ![]() не
в середине, а на левой и правой границах
элементарных отрезков соответственно.
Абсолютная
погрешность методов левых и правых
прямоугольников оценивается как
не
в середине, а на левой и правой границах
элементарных отрезков соответственно.
Абсолютная
погрешность методов левых и правых
прямоугольников оценивается как  .
.
101-103. Дифференциальное уравнение (ДУ) – это уравнение, в которое входит неизвестная функция под знаком производной или дифференциала. Если неизвестная функция является функцией одной переменной, то дифференциальное уравнение называют обыкновенным (сокращенно ОДУ – обыкновенное дифференциальное уравнение). Если же неизвестная функция есть функция многих переменных, то дифференциальное уравнение называют уравнением в частных производных.
Решение дифференциального уравнения - это неявно заданная функция Ф(x, y) = 0 (в некоторых случаях функцию y можно выразить через аргумент x явно), которая обращает дифференциальное уравнение в тождество.
Общим решением ДУ, называют такое решение, которое содержит произвольную постоянную.
Частным решением ДУ называется решение, полученное при определенных начальных условиях.
Порядком ДУ- называется порядок его старшей производной.
Общее
решение дифференциальных уравнений
вида ![]() на
заданном интервале X можно
отыскать, проинтегрировав обе части
этого равенства. Получим
на
заданном интервале X можно
отыскать, проинтегрировав обе части
этого равенства. Получим ![]() .
Если обратиться ксвойствам
неопределенного интеграла,
то придем к искомому общему решению y
= F(x) + C,
где F(x) –
одна из первообразных функции f(x) на
промежутке X,
а С –
произвольная постоянная.
Заметим,
что во многих задачах интервал X не
указывается. В этом случае подразумевается,
что решение следует искать для всех x,
при которых и искомая функция y,
и исходное уравнение имеют смысл.
Если
требуется найти частное решение
дифференциального уравнения
.
Если обратиться ксвойствам
неопределенного интеграла,
то придем к искомому общему решению y
= F(x) + C,
где F(x) –
одна из первообразных функции f(x) на
промежутке X,
а С –
произвольная постоянная.
Заметим,
что во многих задачах интервал X не
указывается. В этом случае подразумевается,
что решение следует искать для всех x,
при которых и искомая функция y,
и исходное уравнение имеют смысл.
Если
требуется найти частное решение
дифференциального уравнения ![]() ,
удовлетворяющее начальному условию y(x0)
= y0,
то после нахождения общего интеграла y
= F(x) + C,
еще нужно вычислить значение постоянной C
= C0,
используя начальное условие. То есть,
константа C
= C0определяется
из уравнения F(x0)
+ C = y0,
и искомое частное решение дифференциального
уравнения будет иметь вид y
= F(x) + C0.
Рассмотрим пример.
Пример.
Найдите
общее решение дифференциального
уравнения
,
удовлетворяющее начальному условию y(x0)
= y0,
то после нахождения общего интеграла y
= F(x) + C,
еще нужно вычислить значение постоянной C
= C0,
используя начальное условие. То есть,
константа C
= C0определяется
из уравнения F(x0)
+ C = y0,
и искомое частное решение дифференциального
уравнения будет иметь вид y
= F(x) + C0.
Рассмотрим пример.
Пример.
Найдите
общее решение дифференциального
уравнения ![]() ,
проверьте правильность результата.
Найдите частное решение этого уравнения,
удовлетворяющее начальному
условию
,
проверьте правильность результата.
Найдите частное решение этого уравнения,
удовлетворяющее начальному
условию  .
Решение.
Проинтегрировав
исходное дифференциальное уравнение,
получим
.
Решение.
Проинтегрировав
исходное дифференциальное уравнение,
получим ![]() .
Этот интеграл возьмем методом интегрирования
по частям:
.
Этот интеграл возьмем методом интегрирования
по частям:
 Таким
образом,
Таким
образом,  -
общее решение дифференциального
уравнения.
-
общее решение дифференциального
уравнения.
-
. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
 .
ЛОДУ
с постоянными коэффициентами является
очень распространенным видом
дифференциальных уравнений. Их решение
не представляет особой сложности.
Сначала отыскиваются корни
характеристического уравнения
.
ЛОДУ
с постоянными коэффициентами является
очень распространенным видом
дифференциальных уравнений. Их решение
не представляет особой сложности.
Сначала отыскиваются корни
характеристического уравнения  .
При различных p и qвозможны
три случая: корни характеристического
уравнения могут быть действительными
и различающимися
.
При различных p и qвозможны
три случая: корни характеристического
уравнения могут быть действительными
и различающимися 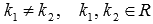 ,
действительными и совпадающими
,
действительными и совпадающими 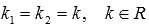 или
комплексно сопряженными
или
комплексно сопряженными 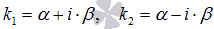 .
В зависимости от значений корней
характеристического уравнения,
записывается общее решение дифференциального
уравнения как
.
В зависимости от значений корней
характеристического уравнения,
записывается общее решение дифференциального
уравнения как  ,
или
,
или 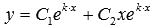 ,
или
,
или 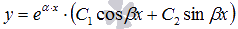 соответственно.
Для
примера рассмотрим линейное однородное
дифференциальное уравнение второго
порядка с постоянными коэффициентами
соответственно.
Для
примера рассмотрим линейное однородное
дифференциальное уравнение второго
порядка с постоянными коэффициентами  .
Корнями его характеристического
уравнения
.
Корнями его характеристического
уравнения 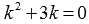 являются k 1 =
-3 и k 2 =
0.
Корни действительные и различные,
следовательно, общее решение ЛОДУ с
постоянными коэффициентами имеет
вид
являются k 1 =
-3 и k 2 =
0.
Корни действительные и различные,
следовательно, общее решение ЛОДУ с
постоянными коэффициентами имеет
вид
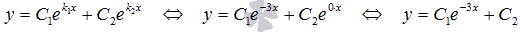
-
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
 .
Общее
решение ЛНДУ второго порядка с постоянными
коэффициентами y ищется
в виде суммы
.
Общее
решение ЛНДУ второго порядка с постоянными
коэффициентами y ищется
в виде суммы  общего
решения соответствующего ЛОДУ
общего
решения соответствующего ЛОДУ 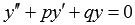 и
частного решения
и
частного решения исходного
неоднородного уравнения, то есть,
исходного
неоднородного уравнения, то есть, 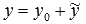 .
Нахождению общего решения однородного
дифференциального уравнения с постоянными
коэффициентами
.
Нахождению общего решения однородного
дифференциального уравнения с постоянными
коэффициентами  ,
посвящен предыдущий пункт. А частное
решение
,
посвящен предыдущий пункт. А частное
решение 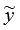 определяется
либо методом неопределенных коэффициентов
при определенном виде функции f(x),
стоящей в правой части исходного
уравнения, либо методом вариации
произвольных постоянных.
В
качестве примеров ЛНДУ второго порядка
с постоянными коэффициентами
приведем
определяется
либо методом неопределенных коэффициентов
при определенном виде функции f(x),
стоящей в правой части исходного
уравнения, либо методом вариации
произвольных постоянных.
В
качестве примеров ЛНДУ второго порядка
с постоянными коэффициентами
приведем
 Линейные
однородные дифференциальные уравнения
(ЛОДУ)
Линейные
однородные дифференциальные уравнения
(ЛОДУ)  и
линейные неоднородные дифференциальные
уравнения (ЛНДУ) второго порядка
и
линейные неоднородные дифференциальные
уравнения (ЛНДУ) второго порядка 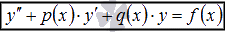 .
.
104.
КОШИ ЗАДАЧА
-
одна из основных задач теории
дифференциальных уравнений (обыкновенных
и с частными производными); состоит в
отыскании решения (интеграла)
дифференциального уравнения,
удовлетворяющего так наз. начальным
условиям (начальным данным). К. з. обычно
возникает при анализе процессов,
определяемых дифференциальным законом
и начальным состоянием, математич.
выражением к-рых и являются уравнение
и начальное условие (откуда терминология
и выбор обозначений: начальные данные
задаются при (=0, а решение отыскивается
при ![]() ).
От краевых задач К. з. отличается тем,
что область, в к-рой должно быть определено
искомое решение, здесь заранее не
указывается. Тем не менее и К. з. можно
рассматривать как одну из краевых задач.
).
От краевых задач К. з. отличается тем,
что область, в к-рой должно быть определено
искомое решение, здесь заранее не
указывается. Тем не менее и К. з. можно
рассматривать как одну из краевых задач.
Основные вопросы, к-рые связаны с К. з., таковы.
1) Существует ли (хотя бы локально) решение К. з.?
2) Если решение существует, то какому пространству оно принадлежит, в частности, какова область его существования?
3) Является ли решение единственным?
4) Если решение единственно, то будет ли оно корректным, т. е. непрерывным (в каком-либо смысле) относительно начальных данных?
Простейшая
К. з. состоит в том, что требуется найти
определенную на полупрямой ![]() функцию
и(х), к-рая
удовлетворяет обыкновенному
дифференциальному уравнению 1-го порядка
функцию
и(х), к-рая
удовлетворяет обыкновенному
дифференциальному уравнению 1-го порядка
![]()
(а - данная функция) и при х=х 0 принимает значение и 0:
![]()
Геометрически это означает, что в семействе интегральных кривых уравнения (1) на плоскости ( х, и).разыскивается кривая, преходящая через точку ( х 0, u0).
Первое утверждение о существовании такой функции (при условии непрерывности f для всех хи непрерывной дифференцнруемости ее по и).доказано О. Коши (A.Cauchy, 1820-30) и обобщено Э. Пикаром (Е. Picard, 1891-96) (заменившим дифференцируемость условием Липшица по и). При этом решение К. з. оказывается единственным и непрерывно зависящим от начальных данных. Современные представления о К. з. - по существу далеко идущее обобщение этой задачи.
То, что вопросы 1) - 4) глубоко затрагивают суть дела, т. е. для утвердительного ответа на них требуются определенные условия, иллюстрируется уже теорией обыкновенных дифференциальных уравнений. Так, решение К. з. для уравнения (1) с условием (2), где f задана на открытом множестве G и лишь непрерывна, существует на нек-ром интервале, зависящем от Gи (х 0, u0) (см.Пеана теорема), но может быть неединственным. Решение может существовать не во всех точках, где определено f.
Дословно так же формулируется К. з. для систем обыкновенных дифференциальных уравнений, т. е. для обыкновенного дифференциального уравнения вида (1) с начальным условием (2), где и=и (х).- функция со значением в конечномерном векторном пространстве
![]() -
функция, определенная в
-
функция, определенная в ![]() Для
существования, единственности и
корректности решения К. з. и здесь
достаточны условия Пикара.
Для
существования, единственности и
корректности решения К. з. и здесь
достаточны условия Пикара.
Для обыкновенных дифференциальных уравнений высших порядков
![]()
К. з ., в начальных данных к-рой участвуют, помимо самой функции, и ее производные
![]()
стандартным приемом сводится к соответствующей задаче вида (1), (2).
В случае обыкновенных дифференциальных уравнений 1-го порядка, не разрешимых относительно производной искомой функции, постановка К. з.- та же, разве что в большей степени опирается на ее геометрич. трактовку, но исследование может осложняться невозможностью (даже локальной) редукции уравнения к нормальной форме (1).
Если для обыкновенного дифференциального уравнения постановка и исследование К. з. не содержит принципиальных затруднений, то в случае дифференциальных уравнений с частными производными положение (и, в частности, ответы на вопросы 1) - 4)) существенно усложняется, даже если рассматриваемые функции достаточно регулярны. Это в значительной мере обусловлено многомерностъю пространства независимых переменных и вытекающими из этого (алгебраическими) вопросами разрешимости. Так, условие разрешимости К. з. (в нек-ром смысле промежуточной между "обыкновенностью" и "частностью") для системы уравнений в полных дифференциалах

состоящей в отыскании ( п-k )-мерной интегральной поверхности, проходящей через данную точку, имеет вид
![]()
(в
окрестности этой точки; здесь d,![]() - символы
внешнего дифференциала и внешнего
произведения соответственно) (см.Фробениуса
теорема).
- символы
внешнего дифференциала и внешнего
произведения соответственно) (см.Фробениуса
теорема).
Для линейных дифференциальных уравнений с частными производными

К. з. ставится следующим образом. В нек-рой области Gпеременных х=( х 1,. . . , х п). найти решение, удовлетворяющее начальным условиям, т, е, принимающее вместе со своими производными до (та-1)-го порядка включительно заданные значения на нек-рой расположенной в G (n-1)-мерной гиперповерхности S(носители начальных условий). Начальные условия можно задавать в виде производных от ипо направлению единичной нормали v к S:

где ![]() -
известные функции (данные К о ш и).
Аналогичным образом ставится К. з. и для
нелинейных дифференциальных уравнений.
С К. з. связано понятие нехарактеристич.
поверхности. Если неособое преобразование
переменных
-
известные функции (данные К о ш и).
Аналогичным образом ставится К. з. и для
нелинейных дифференциальных уравнений.
С К. з. связано понятие нехарактеристич.
поверхности. Если неособое преобразование
переменных ![]() "
выпрямляет" поверхность Sв окрестности
точки х 0, переводя
ее в участок гиперплоскости
"
выпрямляет" поверхность Sв окрестности
точки х 0, переводя
ее в участок гиперплоскости ![]() то
в преобразованном уравнении (3) коэффициент
при
то
в преобразованном уравнении (3) коэффициент
при ![]() пропорционален
величине
пропорционален
величине

Поверхность Sназ. нехарактеристической в точке х 0, если
![]()
В этом случае вблизи точки х 0 уравнений (3) можно записать в так наз. нормальной форме

К.
з. обычно рассматривается, когда носителем
начальных данных является характеристич.
поверхность, т. е.
когда условие (5) выполнено для всех ![]()
В
теории К. з. важное место занимает Коши
- Ковалевской теорема:если S
- аналитич.
поверхность в окрестности своей
точки х 0,функции ![]() аналитичны
в этой окрестности и выполнено условие
(5), то в окрестности точки существует
аналитич. решение и(х).К. з. (3), (4), к-рое в
классе аналитич. функций единственно.
В предположении аналитичности эта
теорема справедлива и для общих нелинейных
уравнений, если они могут быть приведены
к нормальной форме (6), а также для систем
таких уравнений. Эта теорема носит
универсальный характер, поскольку она
применима аналитич. уравнениям независимо
от их типа (эллиптического, гиперболического
и т. д.) и дает существование решения в
малом. Решение единственно в классе
неаналитич. функций.
аналитичны
в этой окрестности и выполнено условие
(5), то в окрестности точки существует
аналитич. решение и(х).К. з. (3), (4), к-рое в
классе аналитич. функций единственно.
В предположении аналитичности эта
теорема справедлива и для общих нелинейных
уравнений, если они могут быть приведены
к нормальной форме (6), а также для систем
таких уравнений. Эта теорема носит
универсальный характер, поскольку она
применима аналитич. уравнениям независимо
от их типа (эллиптического, гиперболического
и т. д.) и дает существование решения в
малом. Решение единственно в классе
неаналитич. функций.
Для дифференциальных уравнений с частными производными порядка выше 1-го К. з. может оказаться некорректной, если в условиях теоремы Коши - Ковалевской отказаться от аналитичности уравнения или данных Коши. Иллюстрацией служит пример А д а м а р а: К. з. для уравнения Лапласа
![]()
с начальными условиями
![]()
не
имеет решения, если функция ![]() не
является аналитической.
не
является аналитической.
105.
Пусть ![]() —
некоторая функция,
—
некоторая функция, ![]() —
ее производная. Для удобства будем
записывать производную виде
—
ее производная. Для удобства будем
записывать производную виде ![]() ,
имеющем смысл отношения бесконечно
малых приращений — дифференциалов.
Дифференциал
,
имеющем смысл отношения бесконечно
малых приращений — дифференциалов.
Дифференциал ![]() —
приращение значения переменной в
окрестности
—
приращение значения переменной в
окрестности ![]() ,
стремящееся к нулю. Дифференциал
функции
,
стремящееся к нулю. Дифференциал
функции ![]() —
малое приращение функции,
—
малое приращение функции, ![]() .
Пусть
.
Пусть ![]() и
и ![]() —
некоторые функции от
—
некоторые функции от ![]() и
и ![]() .
Рассмотрим уравнение
.
Рассмотрим уравнение
![]() .
.
Уравнение
такого вида называется обыкновенным
дифференциальным уравнением с
разделяющимися переменными. Умножим
его на ![]() :
:
![]() .
.
Последнее
равенство означает, что малые приращения
левой и правой частей равны. Поэтому их
суммы также равны. Предположим что
при ![]()
![]() и
возьмем интегралы от левой и правой
частей. Пределы интегрирования —
от
и
возьмем интегралы от левой и правой
частей. Пределы интегрирования —
от ![]() до
до ![]() для
левой части и от
для
левой части и от ![]() для
для ![]() для
правой части уравнения:
для
правой части уравнения:
 .
.
Решая
получившееся в результате интегрирования
алгебраическое уравнение, мы можем
выразить ![]() .
.
Значения ![]() и
и ![]() называются
начальными условиями. В случае других
начальных условий решение уравнения
будет отличаться на постоянную. Поэтому,
если начальные условия не даны, можно
взять первообразные левой и правой
частей и прибавить к ним константу.
Используя неопределенный интеграл —
обозначение множества первообразных
—
называются
начальными условиями. В случае других
начальных условий решение уравнения
будет отличаться на постоянную. Поэтому,
если начальные условия не даны, можно
взять первообразные левой и правой
частей и прибавить к ним константу.
Используя неопределенный интеграл —
обозначение множества первообразных
— ![]() ,
где
,
где ![]() —
первообразная
—
первообразная ![]() ,
, ![]() —
произвольная постоянная, запишем это
в виде
—
произвольная постоянная, запишем это
в виде
