Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ульяновский Государственный Педагогический Университет им. И. Н. Ульянова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ankilov

.pdf

Скачиваний:

Добавлен:

07.02.2015

Размер:

2.14 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 2814 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

			(x 3)2n 1
Пример 5.2.3. Найдем область сходимости ряда						.
Пример 5.2.3. Найдем область сходимости ряда			n	2	1	.
		n 0	n		1
Для данного ряда последовательность	an	не определена, так как все коэффициенты
Для данного ряда последовательность		не определена, так как все коэффициенты
	an 1

ряда с четными номерами равны нулю. Обозначим через U n (x) n-й член данного ряда и

x 3

2n 1

применим к ряду

U n (x)

признак Даламбера. Имеем:

n 0

lim

U n 1

(x)

lim

x 3

2n 3

n2 1

x 3

lim

n2 1

x 3

U n (x)

2n 1

(n 1)2 1

x 3

n (n 1)2

Если

x 3

1, то на основании признака Даламбера и теоремы 5.1.8 исходный ряд

U n 1 x

U n x

U n (x)

сходится

абсолютно. Если

x 3

2 1,

то

для

достаточно

n 0

больших n, следовательно,

limU n (x) 0

расходится.

и ряд U n (x)

n 0

Решая неравенство

x 3

2 1, получаем интервал

сходимости

(2,4).

Исследуем

сходимость ряда на концах этого интервала. При

x 4 получаем ряд

, который

n 0

сходится,

так как

, а

– сходящийся

ряд.

При x 2

получим ряд

n 0

2n 1

( 1)

, который также сходится.

n 0

n 1

n 0 n

Таким образом, отрезок [2, 4] – область сходимости данного степенного ряда.

В ряде случаев вместо признака Даламбера более удобным оказывается применение радикального признака Коши. Соответствующая формула для вычисления радиуса сходимости дается следующей теоремой.

Теорема 5.2.3. Если существует предел

lim n

l ,

то

радиус

сходимости степенного

ряда

(5.7)

или (5.8)

находится

по формуле

1 lim

. При этом R 0 , если l и R ,

если l 0 .

n n

x n

Пример

5.2.4.

Рассмотрим

ряд

Здесь

следовательно,

n 1

l lim n

lim n

lim 1 0 , а тогда R .

n n

Ряд сходится на всей числовой оси, т. е. при любом x ( , ) .

131

5.2.2. Разложение функций в степенные ряды

Сумма степенного ряда является функцией от переменной x:


f (x) an xn .		(5.10)
	n 0
Если интервал сходимости этого	ряда ( R, R) , то говорят, что функция	f (x)
разлагается в степенной ряд в интервале	( R, R) . Для получения разложений функций в

степенные ряды часто используются следующие свойства сходящихся степенных рядов:

1. Степенной ряд в интервале его сходимости можно почленно дифференцировать, т. е. если имеет место разложение (5.10), то для всех x ( R, R)


f / (x) nan xn 1 .	(5.11)
n 1

При этом радиусы сходимости рядов (5.10) и (5.11) совпадают.

Отсюда следует, что сумма степенного ряда является бесконечно дифференцируемой функцией.

2. Степенной ряд в интервале его сходимости можно почленно интегрировать, т. е. для любых x0, x ( R, R) из равенства (5.10) следует равенство

x			xn 1 x0n 1
f (t)dt an						.
f (t)dt an				n 1		.
x0	n 0			n 1
x0
В частности, при x0 0 имеем
x		x		n 1
f (t)dt an		x			.	(5.12)
f (t)dt an		n 1			.	(5.12)
0	n 0	n 1

Радиусы сходимости рядов (5.10) и (5.12) совпадают.

Теорема 5.2.4. Если функция f (x) разлагается в степенной ряд (5.10) в интервале ( R, R) , то это разложение единственно, а его коэффициенты находятся по формулам

an			f n (0)	,		n = 0,1,2,….			(5.13)
an			n!	,		n = 0,1,2,….			(5.13)
			n!
Доказательство. По условию теоремы в интервале ( R, R)
f (x) a	0	a x a		2	x2	... a	n	xn ... .	(5.14)
	0		1	2			n

По свойству 1 степенной ряд (5.14) можно почленно дифференцировать в интервале ( R, R) любое число раз. Дифференцируя, получаем

f / (x) 1 a	2a	2	x 3a	3	x2	... na	n	xn 1	... ,
1		2		3			n
f // (x) 2 1a2	3 2a3 x ... n(n 1)an xn 2									...,

f /// (x) 3 2 1a3 4 3 2a4 x ... n(n 1)(n 2)an xn 3 ... ,

. . . . . . . . . . . . . . . . . .

f n (x) n!an (n 1)n...3 2an 1 x ... .

. . . . . . . . . . . . . . . . . .

Полагая в полученных равенствах и в равенстве (5.14) x 0 , имеем

132

f (0) a

f /

(0) 1!a ,

f // (0)

2!a

откуда находим

f /// (0) 3!a3 ,…,

f n (0) n!an ,…,

f (0) , a

/ (0)

// (0)

, a

f /// (0)

,…, a

n (0)

,…,

т. е. an

f n (0)

, n = 0,1,2,….

Таким образом, коэффициенты ряда (5.10) определяются единственным образом

формулами (5.13), что и доказывает теорему.

Подставляя полученные выражения коэффициентов в (5.10), получаем

(0)

(n)

(0)

(n)

(0)

f (x) f (0)

...

xn ...

xn .

n 0

Итак, если функция f (x)

разлагается в степенной ряд, то этот ряд имеет вид

(0)

(n)

(0)

(n)

(0)

f (0)

...

xn ...

xn .

(5.15)

n 0

Ряд (5.15) называется рядом Тейлора для функции

f (x) .

Пусть теперь f (x)

– произвольная бесконечно дифференцируемая в интервале ( R, R)

функция. Для нее можно составить ряд (5.15). Установим, при каких условиях сумма ряда

(5.15) совпадает с функцией f (x) . Ответ на этот вопрос можно получить										с помощью
формулы Тейлора
f (x) f (0)	f / (0)		x	f // (0)		x2	...	f (n) (0)	xn Rn (x) ,	(5.16)
f (x) f (0)			x			x2	...		xn Rn (x) ,	(5.16)
	1!	2!						n!
где
Rn (x)		f (n 1) ( x)			xn 1 ,		0 1.
Rn (x)					xn 1 ,		0 1.
		(n 1)!

Если обозначим через Sn (x) частичную сумму ряда (5.15), то формулу (5.16) можно записать в виде

f (x) Sn (x) Rn (x) .

Отсюда следует, что lim Sn (x) f (x)	тогда и только тогда, когда lim Rn (x) 0 . Таким
n	n
образом, доказана

Теорема 5.2.5. Пусть f (x) – бесконечно дифференцируемая функция в интервале ( R, R) . Тогда для того, чтобы ряд Тейлора (5.15) сходился в ( R, R) и имел своей суммой функцию f (x) , необходимо и достаточно, чтобы остаточный член Rn (x) формулы Тейлора

(5.16) стремился к нулю в указанном интервале при n , т. е. lim Rn (x) 0 для любого

x ( R, R) .

133

Все сказанное выше о разложении функций в степенные ряды относительно переменной x переносится на степенные ряды по степеням x a . В этом случае разложение функции в ряд Тейлора имеет вид

		(n)	(a)
f (x)	f			(x a)n .	(5.17)
		n!
n 0

Ряд (5.15), являющийся частным случаем ряда (5.17), часто называют рядом Маклорена или рядом Тейлора-Маклорена.

Рассмотрим теперь разложение некоторых элементарных функций в ряд Маклорена. 1. f (x) ex .

Так как f (n) (x) ex , n = 0,1,2,…, то

(n) (0) 1 , и ряд Маклорена (5.15) принимает вид

...

n 0

Можно показать, что lim R

(x) 0

при

любом

x ( , ) , где

(x)

e x

xn 1

–

(n 1)!

остаточный член формулы Тейлора для функции

f (x) ex . По теореме 5.2.5 при любом

x R имеет место разложение

ex 1

...

n 0

2. f (x) sin x .

Вычисляя последовательно производные этой функции, замечаем их повторяемость:

f / (x) cos x ,	f // (x) sin x ,	f /// (x) cos x , f 4 (x) sin x , f 5 (x) cos x f / (x) и т. д.
Следовательно,	f 4k (x) sin x ,	f (4k 1) (x) cos x , f (4k 2) (x) sin x , f (4k 3) (x) cos x .

Отсюда находим f 4k (0) f (4k 2) (0) 0 , f (4k 1) (0) 1 , f (							4k 3) (0) 1. Составим по формуле
(5.15) для функции f (x) sin x ряд Маклорена
x	x3		x5	...	( 1)n	x2n 1	... .
					(2n 1)!
3!		5!

Применяя теорему 5.2.5, можно показать, что на всей числовой оси этот ряд сходится и

имеет своей суммой функцию

f (x) sin x , т. е. при любом x R имеет место разложение

( 1)

2n 1

sin x x

...

x2n 1

... ( 1)n

(2n 1)!

n 0

3. f (x) cos x .

Разложение этой функции легко получается в результате почленного

дифференцирования ряда для sin x :
		x3		x5			1 n x2n 1
sin x	x					...		... ,
sin x	x					...		... ,
			3!		5!		2n 1 !
			3!		5!		2n 1 !

откуда

134

cos x 1

...

2n !

n 0

Полученное разложение справедливо для всех x R . 4. f x 1 x , R. Имеем:

,...,

f x 1 x

f x 1 1

f n x 1 ... n 1 1 x n ,...,

откуда, полагая х=0, получаем f 0 1, f 0

, f 0 1 ,...,

f n 0 1 ... n 1 . Ряд (5.15) запишется в виде

1 x

1 x2

... 1 ... n 1 xn

... .

(5.18)

Пользуясь формулой (5.9), найдем радиус сходимости этого ряда

1 ... n 1

n 1 !

n 1

R lim

lim

1 ,

1 ... n 1 n

an 1

следовательно, ряд (5.18) сходится в интервале (–1,1). Можно также показать, что его сумма f(x)=(1+х)α, т. е.

1 x

...

1 ... n 1

... 1

1 ... n 1

, x ( 1,1)

1 x

n 1

В частности, при α = –1 получим

1 x x2 ... 1 n xn ...

1 n xn .

(5.19)

1 x

n 0

Заметим, что если α=1,2,3,…, то функция (1+х)α раскладывается по биному Ньютона в многочлен, причем разложение имеет место для любого x R.

5. f x ln 1 x .

Интегрируя равенство (5.19) в пределах от 0 до х (при х 1), получим

x 1 t t 2

t 3 ... 1 n t n ... dt ,

1 t

или

n xn 1

xn 1

ln 1 x x

... 1

(5.20)

n 1

n 0

Это разложение справедливо в интервале (–1,1).

В заключение отметим, что степенные ряды имеют разнообразные приложения. С их помощью с любой заданной точностью вычисляют значения функций (в частности, значенияи е); находят приближенные значения определенных интегралов в тех случаях, когда первообразная не выражается через элементарные функции или ее трудно найти. Так,

например, точное значение интеграла a	sin xdx найти не удается, так как первообразная
0	x

135

функции

sin x

не является элементарной функцией. В то же время эта первообразная легко

выражается в виде степенного ряда. Действительно, посколькуsin x x

..., то

sin x

... ,

причем ряд сходится при любом х. Интегрируя его почленно от 0 до а, имеем

a sin x dx a

....

3!3

5!5

С помощью этого равенства можно при любом а с любой степенью точности вычислить данный интеграл.

Наконец, значительную роль играют степенные ряды в приближенных методах решений дифференциальных уравнений.

5.3.Ряды Фурье

5.3.1.Тригонометрический ряд. Ортогональность основной тригонометрической системы

Определение 5.3.1. Ряд вида:

cos x b sin x a

cos 2x b

sin 2x ... a

cos nx b

sin nx ...

а0

(5.21)

an cos nx bn sin nx

n 1

называется

тригонометрическим

рядом;

а числа

a0 , a1 ,b1 , a2 ,b2 ,..., an ,bn ,...

–

коэффициентами тригонометрического ряда.

В отличие от степенного ряда, рассмотренного в подразделе 5.2, в тригонометрическом ряде вместо простейших функций 1, x, x2 ,..., xn ,... взяты тригонометрические функции

1 2, cos x,sin x, cos 2x,sin 2x,..., cos nx,sin nx,...,

(5.22)

которые также хорошо изучены.

Система функций (5.22) называется основной тригонометрической системой. Прежде всего отметим, что все функции системы (5.22) являются периодическими с периодом Т = 2π. Поэтому любая частичная сумма ряда (5.21) 2π – периодична (если все члены ряда не меняются от замены x на x + 2π, то и сумма его не изменяется от этой замены). Отсюда

следует, что если ряд (5.21) сходится на отрезке –π, π , то он сходится на всей числовой прямой, и его сумма, будучи пределом последовательности частичных сумм, является периодической функцией с периодом Т = 2π. По этой причине тригонометрические ряды особенно удобны при изучении периодических функций, описывающих различные периодические процессы. Примерами периодических процессов служат колебательные и вращательные движения различных деталей машин и приборов, периодическое движение небесных тел и элементарных частиц, акустические и электромагнитные колебания и др.

136

Другим важным свойством функций системы (5.22) является их ортогональность на

отрезке –π, π в следующем смысле: интеграл по отрезку –π, π от произведения любых двух различных функций этой системы равен нулю. Действительно,

								1 cos kxdx				1
												1	sin kx				0 ;
											2k		sin kx				0 ;
								2			2k
																											(5.23)
							1 sin kxdx					1
												1		cos kx			0 .
												2k		cos kx			0 .
							2					2k
Далее:
	1	cos k n x cos k n x dx										1	sin k n x						sin k n x
	1											1	sin k n x						sin k n x
cos kx cos nxdx	2											2		k n							k n				0	при k n .


Если k = n, то
					2	nxdx			1								1			sin 2nx					.		(5.24)
					2				1								1			sin 2nx
cos kx cos nxdx cos										1 cos 2nx dx								x			2n
									2								2
									2								2
Аналогично находим
										0 приk n
				sin kxsin nxdx														.									(5.25)
										приk						n.
Наконец,

								sin kx cos nxdx 0,																			(5.26)

так как																cos k n x							cos k n x
			1	sin k n x sin k n x dx											1
			1												1
sin kx cos nxdx			2												2			k n						k n			0


при k n . Если k = n, то
									1							1
			sin kx cos nxdx							sin 2nxdx							cos 2nx					0 .

									2							4n

Замечание. Аналогичные выкладки показывают, что функции системы (5.22) ортогональны на любом отрезке длиной 2π.

5.3.2. Ряд Фурье. Сходимость ряда Фурье

Для тригонометрического ряда имеет место теорема разложения, аналогичная теореме

5.2.4.

Теорема 5.3.1. Пусть 2π-периодическая функция f(x) интегрируема на отрезке –π, π . Тогда, если на отрезке –π, π функция f(x) разлагается в тригонометрический ряд

f x a0
f x a0	an cos nx bn sin nx ,	(5.27)
2	n 1

137

который можно интегрировать почленно, то это разложение единственно, а его коэффициенты находятся по формулам:

	1
an	1	f x cos nxdx,	n 0,1,2,...,	(5.28)
an		f x cos nxdx,	n 0,1,2,...,	(5.28)


	1
bn	1	f x sin nxdx,	n 1,2,3,....	(5.29)
bn		f x sin nxdx,	n 1,2,3,....	(5.29)

Доказательство. Интегрируя (5.27) по отрезку –π, π , получаем

	a0
f x dx	a0	dx an cos nxdx bn sin nxdx ,
f x dx	2	dx an cos nxdx bn sin nxdx ,
	2		n 1

откуда, учитывая (5.23), находим:

a0 1 f x dx.

Для определения коэффициента ak при coskx (k – натуральное число) умножим

равенство (5.27) на coskx и проинтегрируем по x от –π до π. Тогда на основании формул

(5.23)–(5.26) получаем:

	a0
f x cos kxdx	a0	cos kxdx an
f x cos kxdx	2	cos kxdx an
	2		n 1

откуда

ak 1


cos kx cos nxdx bn cos kx sin nxdx ak			cos2 kxdx ak ,


f x cos kxdx,	k 1,2,3,... .

Аналогично, умножая (5.27) на sinkx и интегрируя в пределах от –π до π, на основании тех же формул получаем:


		f x sin kxdx bk ,

откуда находим
	1
bk	1	f x sin kxdx,	k 1,2,3,... .
bk		f x sin kxdx,	k 1,2,3,... .

Таким образом, коэффициенты an и bn ряда (5.27) определяются единственным образом формулами (5.28), (5.29), что и доказывает теорему.

Эта терема дает основание ввести следующее определение.
Определение 5.3.2. Пусть f x	– 2π-периодическая функция, интегрируемая на

отрезке –π, π . Тогда числа an , bn , найденные по формулам (5.28), (5.29), называются коэффициентами Фурье, а тригонометрический ряд

138

a0
a0	an cos nx bn sin nx
2	n 1
с этими коэффициентами называется рядом Фурье функции		f x .
Установим, при каких условиях ряд Фурье функции		f x	сходится к этой функции.
Ответ на поставленный вопрос дает следующая теорема.
Теорема 5.3.2. Пусть 2π-периодическая функция f x и			ее производная
Теорема 5.3.2. Пусть 2π-периодическая функция f x и			ее производная	f x –

непрерывные функции на отрезке –π, π или же имеют на нем конечное число точек разрыва первого рода. Тогда ряд Фурье функции f x сходится на всей числовой прямой, причем его

сумма S x f x , если x – точка непрерывности функции					f x . Если x0 – точка разрыва
f x , то
	S(x0 )	1 f (x0 0) f (x0 0) ,
		2
где f x0	0	lim	f x ,	f x0 0	lim	f x .
	x x0 0			x	x0 0
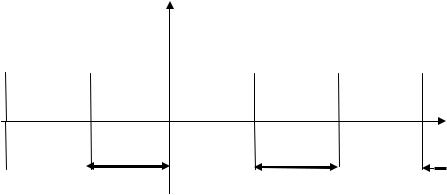
Пример 5.3.1. Периодическая с периодом Т = 2π функции						f x определена следующим
образом:
	f x		1 при x 0
	f x		1 при	0 x .
			1 при	0 x .

Эта функция (рис. 5.1) удовлетворяет условиям теоремы 5.3.2 и, следовательно, может быть разложена в ряд Фурье. Найдем коэффициенты Фурье.

f x

										1									x
– 2						–				1						2		3
											0
											0
												–1
													Рис. 5.1
По формуле (5.28) находим
			1							1	0							sin nx	0
			1							1	0							sin nx	0
an				f x cos nxdx							1 cos nxdx 1 cos nxdx							n
an				f x cos nxdx							1 cos nxdx 1 cos nxdx
															0
															0
	sin nx					0, n	1,2,3,...,
	sin nx
		n			0
		n			0
								1					1	0
						a0			f x dx						1 dx 1 dx		0.
						a0			f x dx						1 dx 1 dx		0.
															0
															0

139

Применяя формулу (5.29), получим

cos nx

f (x) sin nxdx

1 sin nxdx 1 sin nxdx

1 cos n cos n 1

1 cos n

1 1 n ,

n 1,2,3,... .

Разложение (5.27) для данной функции будет

f x

1 1 n

sin 3x

sin 5x

sin 2n 1 x

sin nx

sin x

...

2n 1

n 1

Это равенство справедливо во всех точках,

кроме точек разрыва xk k , k 0, 1, 2,... .

В точках xk k сумма ряда равна

1 f (xk 0) f (xk

0) 0.

f x

Отметим,

что

в силу

2π-периодичности

функции

при

вычислении ее

коэффициентов Фурье по формулам (5.28), (5.29) интегрирование можно выполнять по

любому отрезку длиной 2π, например, по отрезку 0,2π . В некоторых случаях это упрощает процесс нахождения коэффициентов.

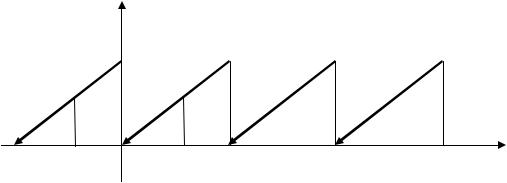
Пример 5.3.2. Пусть требуется разложить в ряд Фурье функцию f x с периодом

Т = 2 π, которая на промежутке 0,2π задана равенством:	f x =x. График функции	f x
изображен на рис. 5.2.
f(x)

		2					0						2								4				6			x
		2					0						2								4				6
													Рис. 5.2
Эта функция на отрезке –π, π задается двумя формулами:																								f x x 2 ,				x ,0 и
f x x,			x (0, ]. В то же время на (0,2π] гораздо проще она задается одной формулой
f x x . Поэтому, интегрируя по отрезку 0,2 , получаем
										1	2		x dx		1		2		1
						a0				1		f			1		xdx		1		x2		02 2 ,
						a0						f					xdx		2		x2		02 2 ,
											0					0			2
			1 2		x cos nxdx			1 2						1				sin nx		2		1 2				1 2
			1 2					1 2						1				sin nx		2		1 2				1 2
an				f					x cos nxdx																		sin nxdx
an				f					x cos nxdx							x				0			sin nxdx				sin nxdx
			0						0									n				n 0				n 0
			0						0									n				n 0				n 0
	cos nx			2	0,
	cos nx			2
	n2			0
	n2			0

140

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 2814 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.02.201581.23 Кб168.docx
#
20.09.2019105.47 Кб18_beR.doc
#
07.02.2015282.72 Кб399-105.docx
#
06.02.2015219.14 Кб17Abl_BH_Met_Flash.doc
#
06.02.201526.62 Кб14about_myself_1.doc
#
07.02.20152.14 Mб36Ankilov.pdf
#
18.11.2019159.23 Кб3Arkhivovedenie-1.doc
#
13.08.2019157.18 Кб3B7.doc
#
20.12.2018451.58 Кб21Batychko_V_T_Trudovoe_pravo_v_voprosah_i_otveta....doc
#
26.04.2019304.13 Кб2bilety_po_yazykoznaniyu_Vosstanovlen.doc
#
05.08.201967.37 Кб2Bilet_ps.docx