
Ankilov
.pdf
3.2.2. Поверхностный интеграл второго рода
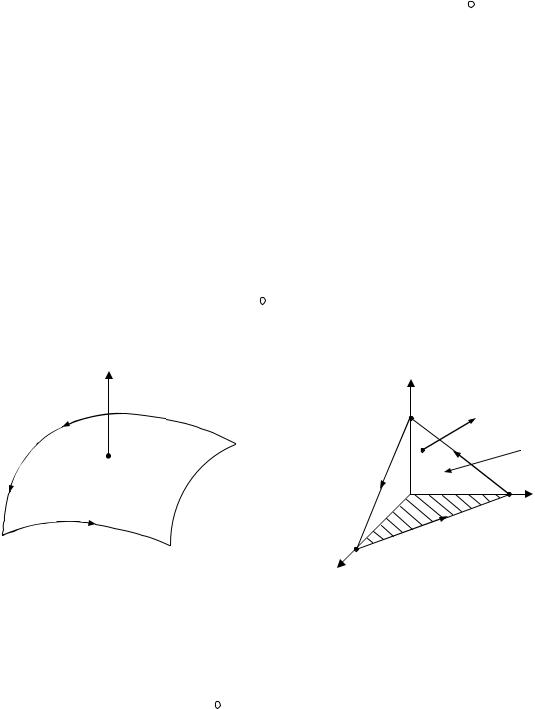
Введем предварительно понятие стороны поверхности. В произвольной точке М гладкой поверхности S фиксируем нормальный вектор (нормаль) n , т. е. вектор, перпендикулярный касательной плоскости к поверхности S в точке М. Рассмотрим на поверхности S какой-либо замкнутый контур, проходящий через точку М и не имеющий общих точек с границей поверхности S. Будем перемещать точку М по замкнутому контуру вместе с вектором n так, чтобы при этом перемещении направление вектора n менялось непрерывно (рис. 3.11). В начальное положение точка М вернется либо с тем же направлением нормали, либо с противоположным.
Если обход по любому замкнутому контуру, лежащему на гладкой поверхности S и не пересекающему ее границу, при возвращении в исходную точку не меняет направление нормали к поверхности, то поверхность называется двусторонней.
Примерами двусторонних поверхностей служат плоскость, сфера, любая поверхность, заданная уравнением z = z(x,y), где z(x, y), zx (x, y), z y (x, y) – функции, непрерывные в
некоторой области D плоскости Оxy.
n
М
S
Рис. 3.11
Если же на гладкой поверхности S существует замкнутый контур, при обходе которого направление нормали меняется после возвращения в исходную точку на противоположное, то поверхность называется односторонней. Простейшим примером односторонней поверхности является так называемый лист Мёбиуса.
В дальнейшем рассматриваются только двусторонние поверхности. Для двусторонней поверхности совокупность всех ее точек с выбранным в них направлением нормали, изменяющимся непрерывно при переходе от точки к точке, называется стороной поверхности.
Перейдем теперь к определению поверхностного интеграла второго рода. Пусть на гладкой поверхности S определены непрерывные функции P(x,y,z), Q(x,y,z), R(x,y,z). Выберем на S определенную сторону и обозначим через n единичный вектор нормали к выбранной
стороне поверхности. Так как n = 1, то n = cos , cos , cos , где α, β, γ – углы, которые вектор n образует с осями координат.
Определение 3.2.4. Поверхностным интегралом второго рода от функций P(x,y,z), Q(x,y,z), R(x,y,z) по выбранной стороне гладкой поверхности S называется число, равное
(P(x, y, z) cos Q(x, y, z) cos R(x, y, z) cos )d . |
(3.26) |
S |
|
Обозначается символом |
|
P(x, y, z)dydz Q(x, y, z)dxdz R(x, y, z)dxdy . |
(3.27) |
S |
|
81
Поверхностный интеграл второго рода по кусочно-гладкой поверхности S определяется как сумма интегралов по гладким кускам, из которых состоит S. Интеграл (3.27) можно также определить как предел соответствующей интегральной суммы.
Поверхностный интеграл второго рода обладает такими же свойствами, как и поверхностный интеграл первого рода, но в отличие от последнего при изменении стороны поверхности (при этом направление нормали n меняется на противоположное) меняет знак.
Выясним физический смысл поверхностного интеграла второго рода. Обозначим через |
||||||||||||||
a вектор с координатами P,Q,R, т. е. |
|
a = P,Q, R . |
Тогда (3.26) можно записать в виде |
|||||||||||
(a, n)d . Согласно определению 3.2.3 |
|
|
|
|
|
|
|
|
|
|
||||
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a, n)d lim |
n |
(a |
, n |
) |
|
, |
(3.28) |
||||||
|
|
i |
||||||||||||
|
|
|
|
0 |
|
i |
i |
|
|
|
||||
S |
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
где i – площадь частичной поверхности i разбиения S на части; ai , ni |
– векторы a и n |
|||||||||||||
в точке M i i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Каждое слагаемое суммы (3.28) |
|
|
|
|
|
|
|
|
|
|
||||
( ai , ni ) i = |
|
ai |
|
cos i i , |
|
i (ai , ni ) |
(3.29) |
|||||||
|
|
|
||||||||||||
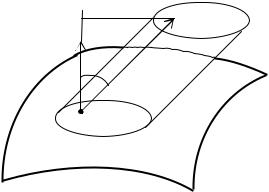
может быть истолковано следующим образом: если i – острый угол, то произведение равно
объему цилиндра с основанием i и высотой |
|
ai |
|
cos i . Пусть вектор a – скорость |
|
|
жидкости, протекающей через поверхность S, тогда произведение (3.29) приближено равно количеству жидкости, протекающей через площадку i за единицу времени в направлении
вектора ni (рис. 3.12).
ni |
ai |
|
φi |
||
|
||
Mi |
|
S
|
|
|
Рис. 3.12 |
|
Следовательно, |
интеграл |
(a, n)d P cos cos R cos )d |
будет |
|
|
|
S |
S |
|
представлять общее количество жидкости, протекающей за единицу времени через поверхность S в направлении вектора n .
Рассмотрим основные способы вычисления поверхностных интегралов второго рода. 1. Если уравнение поверхности S можно представить в виде z = z(x,y), то
R(x, y, z)cos d R(x, y, z)dxdy R(x, y, z(x, y))dxdy , |
(3.30) |
||
S |
S |
D1 |
|
где D1 – проекция поверхности S на плоскость Оxy, знак «+» берется в том случае, когда вектор n образует с осью Оz острый угол (cos 0) , знак «–», если этот угол
тупой(cos 0) .
82
Формула (3.30) позволяет свести вычисление поверхностного интеграла второго рода от функции R(x, y, z) по поверхности S к вычислению двойного интеграла по области D1 – проекцииS на плоскость Оxy.
Аналогично вычисляются интегралы от функций P(x,y,z) и Q(x,y,z): |
|
||
Р(x, y, z)cos d P(x, y, z)dydz P(x( y, z), y, z)dydz, |
(3.31) |
||
S |
S |
D2 |
|
Q x, y, z cos d |
Q x, y, z dxdz Q x, y x, z , z dxdz. |
(3.32) |
|
S |
S |
D3 |
|
Здесь x = x(y,z) и y =y (x,z) – уравнения поверхности S; D2 и D3 – проекции поверхности S на плоскости Оyz и Оxz соответственно.
Таким образом, если из уравнения F (x,y,z) = 0 поверхности S однозначно выражаются z, x, y, то вычисление интеграла (3.27) сводится к применению формул (3.30) – (3.32) и последующему вычислению соответствующих двойных интегралов.
Пример 3.2.3. Вычислить интеграл
xdydz ydxdz zdxdy,
S
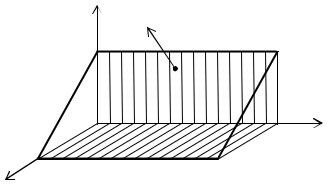
где S – верхняя сторона части плоскости x + z – 1 = 0, отсеченная плоскостями y = 0, y = 4 и лежащая в первом октанте (рис. 3.13).
z |
n |
|
|
1 |
|
|
D2 |
S |
|
|
|
О |
D1 |
4 y |
|
1
x
Рис. 3.13
Решение. Учитывая, что вектор n образует с осями координат острые углы, по формулам (3.30) – (3.32) соответственно находим
zdxdy |
(1 x)dxdy 1 |
dx 4 |
(1 x)dy 41 |
(1 x)dx 2(1 x)2 |
|
10 |
2 , |
|||
|
||||||||||
S |
D1 |
0 |
0 |
0 |
|
|
|
|
|
|
xdydz |
(1 z)dydz 1 |
dz 4 |
(1 z)dy 41 |
(1 z)dz 2(1 z)2 |
|
|
10 |
2 , |
||
|
||||||||||
S |
D2 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
ydxdz y cos d 0 , |
|
|
|
|||||
|
|
S |
|
S |
|
|
|
|
|
|
так как плоскость S параллельна оси Оy ( cos 0). Следовательно,
хdydz ydxdz zdxdy 2 0 2 4 .
S
83
2. Если уравнение поверхности S можно представить в виде z = z(x,y), то |
|
|
Pdydz Qdхdх Rdxdy (R zx P zy Q)dxdy , |
(3.33) |
|
S |
D |
|
где D – проекция поверхности S на плоскость Оxy. В правой части формулы (3.33) переменную z в подынтегральном выражении следует заменить на z(x,y), знак перед интегралом выбирается так же, как в формуле (3.30).
Аналогичные формулы имеют место и в тех случаях, когда уравнение поверхности S может быть представлено в виде x = x(y,z) или y = y(x,z).
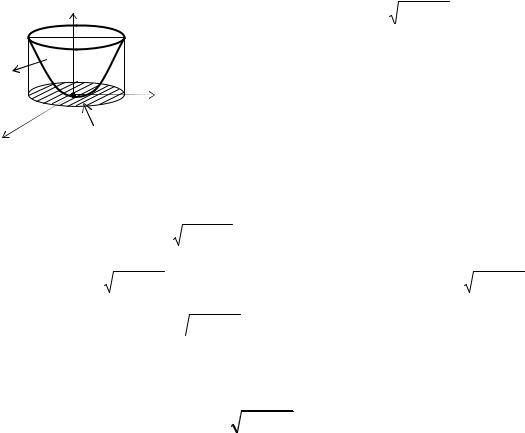
Пример 3.2.4. Вычислить z
1
 S: z = x2 + y2
S: z = x2 + y2
n |
|
O |
y |
|
|
|
|
|
|
|
1 |
|
x |
|
D |
|
|
|
|
|
|
|
Рис. 3.14 |
|
x2 y 2 dxdz 2zdxdy |
S |
|
по внешней |
стороне параболоида вращения |
z = x2+y2 (0 z 1) (рис. 3.14).
Решение. По условию z меняется от 0 до 1. Подставляя z = 1 в уравнение параболоида, получаем x2 + y2 = 1. Значит проекцией поверхности S на плоскость Оxy является круг D : x2 y2 1.
Воспользуемся формулой (3.33), в правой части которой следует взять знак минус, так как нормаль n образует с осью Оz тупой угол.
Учитывая, что P = 0, Q |
x2 y 2 , |
R 2z , |
zx 2x, |
z y 2 y, будет иметь |
||
I |
x2 y 2 dxdz 2zdxy ( 2(x2 y 2 ) 2x 0 2 y |
x2 y 2 )dxdy |
||||
S |
|
|
D |
|
|
|
2 (x2 y 2 y x2 y 2 )dxdy.
x2 y 2 )dxdy.
D
Переходя в полученном двойном интеграле к полярным координатам, находим
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
I 2 (x2 |
y2 y |
|
x2 y2 )dxdy 2 d (r2 r2 sin )rdr |
||||||||||
D |
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
2 |
|
4 |
|
|
1 |
|
1 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|||||||||
2 (1 sin ) |
r |
|
|
|
|
d |
(1 sin )d |
( cos ) |
02 . |
||||
|
|
|
|
0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
0 |
4 |
|
|
|
2 |
0 |
|
2 |
|
|
|||
|
|
|
|
|
|||||||||
3.2.3. Формула Остроградского-Гаусса
Формула Остроградского-Гаусса устанавливает связь между поверхностным интегралом по замкнутой поверхности и тройным интегралом по пространственной области, ограниченной этой поверхностью. Эта формула является пространственным аналогом формулы Грина (3.13), которая связывает криволинейный интеграл по замкнутой кривой с двойным интегралом по плоской области, ограниченной этой кривой.
Теорема 3.2.1. Пусть пространственная область Т ограничена гладкой или кусочногладкой поверхностью S. Если функции P(x,y,z), Q(x,y,z), R(x,y,z) непрерывны вместе со
84

своими частными производными |
|
P |
, |
Q |
, |
R |
|
|
|
|||
|
в замкнутой области Т |
Т S , |
||||||||||
|
x |
y |
z |
|||||||||
|
|
|
|
|
|
|
|
|
||||
место формула Остроградского-Гаусса |
|
|
|
|
|
|
|
|||||
|
P |
Q R |
|
|
|
|
|
|
|
|
||
|
dxdydz (P cos Q cos R cos )d , |
|||||||||||
T |
x |
y |
z |
|
|
|
|
|
S |
|||
где cos ,cos , cos – направляющие косинусы внешней нормали. Формулу (3.34) можно также записать виде
|
|
P |
Q |
R |
|
|
Pdydz Qdxdz Rdxdy. |
|
|
dxdydz |
|||||
|
x |
y |
z |
|
|
||
T |
|
|
S |
|
|||
то имеет
(3.34)
(3.35)
Наиболее просто теорема 3.2.1 доказывается для области Т, граница которой S пересекается с любой прямой, параллельной осям координат, не более чем в двух точках. Идея доказательства заключается в приведении обеих частей формулы (3.34) к двойным интегралам. Для этого в левой части формулы нужно проинтегрировать первое слагаемое по x, второе – по y, а третье – по z. К такому же выражению приводится и правая часть (3.34), если воспользоваться формулами (3.30) – (3.32).
С помощью формулы Остроградского-Гаусса удобно вычислять поверхностные интегралы по замкнутым поверхностям.
Пример 3.2.5. Вычислить интеграл
xdydz 2 ydxdz 3zdxdy,
S
где S – внешняя сторона пирамиды Т, ограниченной плоскостями x + y + z = 1, x = 0, z = 0 (см. рис. 2.15).
Решение. Применяя формулу (3.35), получаем
|
|
|
I xdydz 2 ydxdz 3zdxdy |
(1 2 3)dxdydz 6 dxdydz 6V , |
|||||||||||
|
|
|
|
S |
|
|
|
|
T |
|
T |
|
|
|
|
где |
V – объем пирамиды Т. Так как |
высота |
пирамиды H = 1, а площадь основания |
||||||||||||
Sо |
1 1 1 |
|
1 |
, то V 1 So H 1 , следовательно, I = 6·V = 1. |
|
|
|
|
|
||||||
|
2 |
|
2 |
3 |
6 |
|
|
|
|
|
|
|
|
|
|
|
Пример 3.2.6. Вычислить интеграл |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x3 cos y3 cos z3 cos d , |
|
|
|
|
|
||||
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
где S – внешняя сторона сферы x2 y2 z2 |
R2 . |
|
|
|
|
|
|
||||||||
|
Решение. Согласно формуле (3.34) имеем |
|
|
|
|
|
|
||||||||
|
|
|
|
I x3 cos y3 cos z3 |
cos d 3 x2 y 2 z 2 dxdydz , |
||||||||||
|
|
|
|
S |
|
|
|
|
|
T |
|
|
|
|
|
где Т – шар: x2 y 2 z 2 |
R2 . |
|
|
|
|
|
|
|
|
|
|||||
|
Переходя в тройном интеграле к сферическим координатам, получаем |
||||||||||||||
|
|
|
|
|
|
2 |
2 |
R |
2 |
2 |
R |
5 |
|
||
|
I 3 x2 y 2 z 2 dxdydz 3 d |
|
|
d 4 |
cos d 3 d |
|
|
|
cos d |
||||||
|
|
|
5 |
||||||||||||
|
|
T |
|
|
|
0 |
|
2 |
0 |
0 |
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3R |
5 |
2 |
2d 6R |
5 |
2 12 R5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
5 |
|
0 |
5 |
|
5 |
|
|
|
|
|
|
|
|
|
85
3.2.4. Формула Стокса
Формула Стокса устанавливает связь между поверхностными и криволинейными интегралами.
Теорема 3.2.2. Пусть функции P(x,y,z), Q(x,y,z), R(x,y,z) непрерывны вместе со своими частными производными первого порядка в некоторой пространственной области Т. Тогда для любой гладкой или кусочно-гладкой незамкнутой поверхности S, лежащей в области Т, имеет место формула Стокса
( |
R |
|
Q) cos ( |
P |
|
R ) cos |
Q |
|
P ) cos d Pdx Qdy Rdz , (3.36) |
||
S |
y |
|
z |
z |
|
x |
x |
|
y |
|
C |
где С – контур, ограничивающий поверхность S.
В формуле (3.36) направление обхода контура С должно быть согласовано с направлением нормали n cos , cos , cos следующим образом: если наблюдатель
смотрит с конца нормали n , то он видит обход контура С совершающимся против часовой стрелки (рис. 3.15).
Доказательство теоремы 3.2.2 основано на применении формул (3.30)–(3.32) и формулы Грина (3.13).
Формула Стокса позволяет интеграл по замкнутой пространственной линии С заменить интегралом по поверхности S, «натянутой» на контур интегрирования. В частности, если S – область на плоскости Оxy, ограниченная контуром С, то cos 0, cos 0, cos 1, и
формула Стокса переходит в формулу Грина.
Пример 3.2.7. Вычислить с помощью формулы Стокса интеграл
xy2 dx dy zdz ,
С
где С – линия пересечения плоскости x + y + z = 1 с координатными плоскостями. Обход контура С указан на рис. 3.16.
n |
|
|
z |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
S |
|
|
|
|
|
S: x + y + z = 1 |
||||
|
|
C |
O |
1 |
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
D |
|
|
y |
|
|
|
|
C |
1 |
|
|
|
|
|
|
|
|
|
Рис. 3.15 |
x |
|
Рис. 3.16 |
|
|
|
|
|||
|
|
R |
|
Q |
|
|||||
Решение. В данном случае |
P = xy2, Q = 1, R = z, |
следовательно, |
|
0 , |
||||||
|
|
|
|
|
|
|
y |
|
z |
|
P R 0 ,z x
будем иметь:
Q P 2xy . Подставляя полученные выражения в формулу Стокса (3.36),
x y
Ixy2 dx dy zdz 2 xy cos d ,
СS
где S – часть плоскости x + y + z = 1, лежащая в первом октанте, а интеграл берется по верхней стороне поверхности S. Далее, по формуле (3.30) имеем:
86

xy cos d xydxdy ,
S D
где D – проекция S на плоскость Оxy (треугольник, ограниченный прямыми x = 0, y = 0, y = 1 – x).
Вычисляя полученный двойной интеграл, находим
|
1 |
1 x |
1 |
|
1 |
|
|
I 2 xydxdy 2 xdx ydy x(1 x)2 dx |
|
. |
|||||
12 |
|||||||
D |
0 |
0 |
0 |
|
|||
Из формулы Стокса следует, что если
R |
|
Q |
, |
P |
|
R |
, |
Q |
|
P |
, |
(3.37) |
y |
|
z |
|
z |
|
x |
|
x |
|
y |
|
|
то криволинейный интеграл по любой пространственной замкнутой кривой С равен нулю:
Pdx Qdy Rdz 0 . |
(3.38) |
С |
|
А это значит, что в данном случае криволинейный интеграл не зависит от пути интегрирования. Как и в случае плоской кривой, условия (3.37) являются необходимыми и достаточными для выполнения равенства (3.38).
3.3. Основные термины
Гладкая кривая. Кусочно-гладкая кривая.
Криволинейный интеграл первого рода (по длине дуги). Криволинейный интеграл второго рода (по координатам). Правильная область.
Односвязная область. Касательная плоскость. Гладкая поверхность.
Кусочно-гладкая поверхность. Поверхностный интеграл первого рода. Нормальный вектор.
Сторона поверхности.
Односторонние и двусторонние поверхности. Поверхностный интеграл второго рода.
3.4.Вопросы для самоконтроля
1.Какая кривая называется гладкой (кусочно-гладкой)?
2.Что называется криволинейным интегралом первого рода? Укажите его физический
смысл.
3.Как вычислить криволинейный интеграл первого рода, если линия интегрирования задана параметрически или уравнением у = f(x)?
4.Какие физические величины можно вычислить с помощью криволинейного интеграла первого рода?
5.Как можно геометрически истолковать криволинейный интеграл первого рода?
6.Что называется криволинейным интегралом второго рода и каков его физический
смысл?
7.От чего зависит величина интеграла?
87

8.Какое из двух направлений обхода замкнутого контура считается положительным?
9.Как вычисляется криволинейный интеграл второго рода?
10.Какие интегралы связывает формула Грина?
11.При выполнении какого условия криволинейный интеграл второго рода не зависит от формы пути интегрирования? Чем определяется величина интеграла в этом случае?
12.Какая поверхность называется гладкой (кусочно-гладкой)?
13.Что называется поверхностным интегралом 1-го рода и каков его физический
смысл?
14.Какие физические величины можно вычислить с помощью поверхностного интеграла 1-го рода?
15.Как свести поверхностный интеграл первого рода к двойному интегралу?
16.Какие поверхности называются двусторонними? Что такое сторона поверхности?
17.Как определяется поверхностный интеграл 2-го рода? От чего зависит величина интеграла?
18.Какой физический смысл имеет поверхностный интеграл 2-го рода?
19.Как вычисляется поверхностный интеграл второго рода?
20.Между какими интегралами устанавливает связь формула Остроградского-Гаусса?
21.Какие интегралы связывает формула Стокса? Как выбирается направление нормального вектора в этой формуле?
3.5. Задачи для самостоятельного решения
Задание 1. Вычислить криволинейный интеграл первого рода |
|
Ответы |
||||||||||||||||||||
1. |
x2 yds ; |
C : y |
R2 x2 , 0 x R |
|
|
|
|
|
R4 |
3 |
|
|||||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
y2ds ; C : x a cos t, y a sin t , 0 t 2 |
a3 |
4 |
|
||||||||||||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
C |
ds |
; C : y ch t , 0 x 1 |
|
|
|
|
|
|
2 arctg e |
|
|||||||||||
y2 |
|
|
|
|
|
|
2 |
|||||||||||||||
4. |
exds ; |
C : x ln 1 t 2 , y 2 arctgt t , |
0 t 3 |
12 |
|
|
||||||||||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 2. Вычислить криволинейный интеграл второго рода |
|
Ответы |
||||||||||||||||||||
1. |
y2dx 2xydy ; C : x a cost, y a sin t , 0 t 2 |
0 |
|
|
||||||||||||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
(x2 y2 )dx dy ; C : y x2 , 0 x 2 |
|
|
|
4 15 |
|
||||||||||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
(x y)dx (x y)dy ; C : x a cost, y bsin t , 0 t |
ab |
|
|||||||||||||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
ydx xdy |
; C : y |
x , 1 x 2 |
|
|
|
|
|
|
ln 2 |
|
||||||||||
|
x |
2 |
y |
2 |
|
|
|
|
|
|
|
|
||||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Задание 3. Применяя формулу Грина, вычислить интеграл (контур C |
|
Ответы |
||||||||||||||||||||
обходится в положительном направлении) |
|
|
|
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
1 |
|
|
y |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||
1. |
|
|
|
dx 1 |
|
dy ; C : y x |
1 2 |
, y 1 |
0 |
|
|
|||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
y |
|
|
x |
2 |
|
|
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(2x y 1)dx (x 2 y 1)dy ; C : |
x2 |
|
y2 |
|
|
|
|||||||||||||||
2. |
|
|
|
|
|
1 |
2 ab |
|
||||||||||||||
a |
2 |
b |
2 |
|
||||||||||||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. |
y ex cos y dx ex sin ydy ; C : y sin x , |
y 0 , 0 x |
2 |
|
|
|||||||||||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
88

Задание 4. Вычислить поверхностный интеграл первого рода |
Ответы |
||||||
1. x3d ; S : x y z a (x 0, y 0, z 0) |
|
|
3a5 20 |
||||
|
S |
|
|
|
|
|
|
2. |
(x y z)d ; S : z |
a2 x2 y2 |
|
|
|
a3 |
|
|
S |
|
|
|
|
|
|
3. |
(x2 y2 )d ; S : z2 x2 y2 (0 z 1) |
|
|
(1 2) 2 |
|||
|
S |
|
|
|
|
|
|
Задание 5. Вычислить поверхностный интеграл второго рода (нормаль |
Ответы |
||||||
к поверхности S образует острый угол с осью Oz) |
|
||||||
|
|
||||||
1. |
( y2 z2 )dxdy ; S : z |
1 x2 0 y 1 |
|
|
2 |
||
|
S |
|
|
|
|
|
|
2. |
3xdydz 2 ydxdz zdxdy ; S : x y 2z 1 (x 0, y 0, z 0) |
1 2 |
|||||
|
S |
|
|
|
|
|
|
3. |
xdydz ( y 2z)dxdz (z 2 y)dxdy ; |
S : z |
4 x2 y2 |
16 |
|||
|
S |
|
|
|
|
|
|
4. |
x2 dydz 2xzdxdy ; S : z 1 x2 y2 |
( z 0 ) |
|
|
0 |
||
|
S |
|
|
|
|
|
|
Задание 6. Применяя формулу Остроградского–Гаусса, вычислить |
Ответы |
||||||
интеграл по внешней стороне замкнутой поверхности S |
|||||||
|
|||||||
1. |
xdydz ydxdz zdxdy ; |
S : x2 y 2 a2 , z 0, z H |
3 a2 H |
||||
|
S |
|
|
|
|
|
|
2. |
ez x dydz x y dxdz (xy z)dxdy ; S : x2 |
y2 z2 2x 2 y 1 |
4 3 |
||||
|
S |
|
|
|
|
|
|
3. |
x y dydz y z dxdz (x z)dxdy ; S : z x2 |
y 2 , z 1 |
3 2 |
||||
|
S |
|
|
|
|
|
|
|
|
3.6. Итоговый контроль |
|
||||
|
Изучив тему, студент должен: |
|
|
|
|
||
|
знать: |
|
|
|
|
|
|
определения криволинейных интегралов 1-го и 2-го рода и физический смысл этих интегралов;
правила вычисления криволинейных интегралов 1-го и 2-го рода;
формулу Грина;
условие независимости криволинейного интеграла от пути интегрирования;
определения поверхностных интегралов 1-го и 2-го порядка и физический смысл этих интегралов;
правила вычисления поверхностных интегралов 1-го и 2-го рода;
формулы Стокса и Остроградского-Гаусса;
уметь:
вычислять криволинейные интегралы 1-го и 2-го рода;
применять формулу Грина для вычисления криволинейного интеграла 2-го рода по замкнутой кривой;
вычислять поверхностные интегралы 1-го и 2-го рода;
применять формулу Остроградского-Гаусса для вычисления поверхностного интеграла 2-го рода по замкнутой поверхности;
иметь представление:
о гладких и кусочно-гладких линиях и поверхностях;
об односторонних и двусторонних поверхностях;
об условиях, при которых имеют место формулы Грина, Стокса, Остроградского-
Гаусса.
89

3.6.1.Тест
1.Результат вычисления криволинейного интеграла f (x, y)ds зависит от:
C
а) подынтегральной функции f (x, y) ;
б) линии интегрирования С; в) способа задания линии С; г) направления обхода линии С.
2. Результат вычисления криволинейного интеграла P(x, y)dx Q(x, y)dy зависит от:
C
а) подынтегральных функций P(x, y) , Q(x, y) ;
б) линии интегрирования С; в) способа задания линии С; г) направления обхода линии С.
3. Если C – окружность x 5cos t , y 5sin t 0 t 2 , то криволинейный интеграл
ex y dx x sin y dy равен:
C
а) 0; б) 20 ; в) ;
г) 50 ; д) 25 .
4. Пусть функции P(x, y) и Q(x, y) непрерывны вместе со своими частными
производными Py/ |
и Qx/ в области D . Тогда криволинейный интеграл P(x, y)dx Q(x, y)dy |
|||||||
|
|
|
фиксированных в области D точках A |
и B |
AB |
|
|
|
при произвольно |
не |
зависит |
от линии |
|||||
интегрирования AB D , если: |
|
|
|
|
|
|||
а) |
Q/ |
= P/ в области D ; |
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
|
б) |
Pdx Qdy 0 , где L – произвольный замкнутый контур, |
L D ; |
|
|||||
|
L |
|
|
|
|
|
|
|
в) |
D – односвязная область и Q / |
= P/ в области D . |
|
|
|
|
||
|
|
|
x |
y |
|
|
|
|
5. Площадь |
S области D , ограниченной линией C , |
можно |
найти по |
формуле |
||||
(направление обхода линии C – положительное): |
|
|
|
|
||||
а) |
S ydx ; |
|
|
|
|
|
||
|
|
C |
|
|
|
|
|
|
б) |
S xdy ; |
|
|
|
|
|
||
|
|
C |
|
|
|
|
|
|
в) |
S ydx ; |
|
|
|
|
|
||
|
|
C |
|
|
|
|
|
|
г) |
S |
1 xdy ydx ; |
|
|
|
|
|
|
|
|
2 C |
|
|
|
|
|
|
д) |
S |
1 ydx xdy . |
|
|
|
|
|
|
|
|
2 C |
|
|
|
|
|
|
6. Результат вычисления поверхностного интеграла f (x, y)d зависит от:
S
а) подынтегральной функции f (x, y) ;
90
