Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ульяновский Государственный Педагогический Университет им. И. Н. Ульянова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ankilov

.pdf

Скачиваний:

Добавлен:

07.02.2015

Размер:

2.14 Mб

Скачать

☆

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 2324 / 2824 25 26 27 28 > Следующая >>>

			1							1		3
f2(x)	1	exp	5	x			2		exp	5		x
f2(x)	25		1		2		25						2	2
			1							1			2
		1 exp		x				1		1
			5					1	exp		5	x
			absf2(x)			f2(x)					5
			absf2(x)			f2(x)

					x1 a
				Given
			x1 a			x1 b
			x2 Maximize(absf2 x1)
M2		f2(x2)				M2 7.151746 10 3
M2		f2(x2)				M2 7.151746 10 3
По формуле (7.45) находим
		M2			3
nspr ceil			(b	a)			nspr 334
nspr ceil			(b	a)			nspr 334
	24 2

Запишите целое число n=nspr, обеспечивающее заданную точность 2 . Подставьте

его вместо n. Запишите в свою лабораторную работу значение интеграла ISPr и получившуюся погрешность |I-ISPr|.

4. Метод трапеций.

Введите число точек разбиения отрезка [a, b]

				n 472
следовательно, шаг интегрирования равен
	h		b a		h 0.015254
	h		n		h 0.015254
			n
Вычислим значение интеграла по формуле (7.26)
n	f(a i h)	f[ a (i 1)			h ]
ITr h	f(a i h)	f[ a (i 1)			h ]	ITr 0.76586312
ITr h		2				ITr 0.76586312
i 1

и находим погрешность

I ITr 5.67 10 7

Найдем число точек разбиения n ( n ntr) отрезка [a,b], необходимое для обеспечения точности 2 . Для этого воспользуемся найденным в предыдущем пункте значением M2. По формуле (7.46) находим

	M2		3
ntr ceil		(b a)		ntr 472

	12 2

Запишите целое число n=ntr, обеспечивающее заданную точность 2 . Подставьте

его вместо n. Запишите в свою лабораторную работу значение интеграла ITr и получившуюся погрешность |I-ITr|.

5. Метод Симпсона.

Введите четное число точек разбиения отрезка [a, b]

231

следовательно, шаг интегрирования равен					n 12
следовательно, шаг интегрирования равен
				h b a				h 0.6
				n
Вычислим значение интеграла по формуле (7.30)
	h		n 1				i
IS	h			f(a i h)		( 1)	i		IS 0.76586306
IS	3	f(a)		f(a i h)	3	( 1)		f(b)	IS 0.76586306
	3
			i 1

и находим погрешность

I IS 5.14 10 7

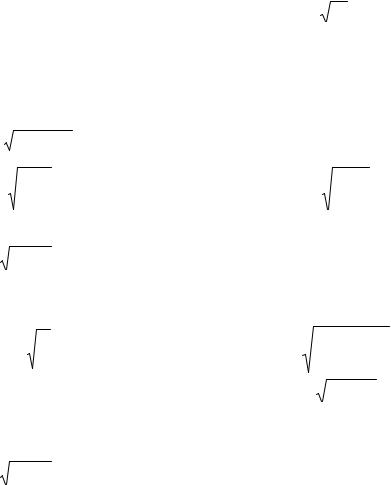
Найдем число точек разбиения n ( n ns) отрезка [a,b], необходимое для обеспечения точности 2 . Для этого найдем максимальное значение модуля четвертой производной (функция f4(x)) M4 на этом отрезке

				1						1	3				1	5				1	7
f4(x)	d4	f(x)	1	exp 5		x		26		exp 5	x			72	exp 5	x			48	exp 5	x
f4(x)	dx4	f(x)	625	1			2	625				2	2	625			2	3	625			2	4
	dx4		625				2	625					2	625				3	625				4
										1					1					1
				1 exp	5	x			1	1					1					1
					5				1	exp	x				1 exp	x				1 exp	x
										5					5					5
										absf4(x)		f4(x)

				x1 a
				Given
			x1 a		x1 b
		x4 Maximize ( absf4				x1)
M4	f4(x4)			M4 1.222355 10 4
M4	f4(x4)			M4 1.222355 10 4
По формуле (7.47) находим		4	M4
		4
					5

			180 2 (b a)
ns ceil			180 2 (b a)			ns 11

Запишите целое число n=ns, обеспечивающее заданную точность 2 . Подставьте

его вместо n. Запишите в свою лабораторную работу значение интеграла IS и получившуюся погрешность |I-IS|.

Вывод: очевидно, что метод Симпсона самый точный, требующий для достижения заданной точности наименьшее число точек разбиения и соответственно вычислений.

Вычисление неопределенных интегралов. Формула НьютонаЛейбница

В системе Mathcad можно вычислять неопределенные интегралы от некоторых классов функций. Например,

f(x) x2 atan(x)

Тогда первообразная

232

	1	x3 atan(x)	1	x2	1	ln 1 x2
f(x) dx

	3		6		6

Необходимо скопировать получившийся результат и подставить в выражение для F(x)

F(x) 13 x3 atan(x) 16 x2 16 ln 1 x2

Если возможно найти какую-нибудь первообразную F(x), то можно вычислить определенный

интеграл по формуле Ньютона-Лейбница				(точный аналитический результат):
b
f(x) dx= F(b) F(a), т.е.
a
a 0		b 1
F(b) F(a)	1		1		1	ln(2)

	12		6		6
	12		6		6

F(b) F(a) 0.210657251225807

7.3.8. Расчетная часть лабораторной работы для тестирующего примера

15,2		x
Вычислить интеграл (7.49):			5
Вычислить интеграл (7.49):	arctg e			dx .
8

1. Разобьем отрезок интегрирования [8;15,2] на 8 частей. Находим шаг интегрирования h 15,28 8 0,9 , и точки разбиения:

x0 8,0; x1 8,9; x2 9,8; x3 10,7; x4 11,6; x5 12,5; x6 13,4; x7 14,3; x8 15,2.

					x
Вычислим в этих точках значения функции				f (x) arctg(e	5 ) и конечные разности yi , 2 yi ,
Вычислим в этих точках значения функции				f (x) arctg(e	5 ) и конечные разности yi , 2 yi ,
3 yi , 4 yi по формулам (7.38). Результаты занесем в табл. 7.11.							Таблица 7.11
		Результаты вычислений		f (x) и конечных разностей			Таблица 7.11
		Результаты вычислений		f (x) и конечных разностей

I	xi	f (xi )	yi	2 yi		3 yi	4 yi
0	8.0	0,199218	– 0,032152	0,005024		– 0,000718	0,000073
1	8.9	0,167066	– 0,027128	0,004306		– 0,000641	0,000075
2	9,8	0,139938	– 0,022822	0,003665		– 0,000566	0,000079
3	10,7	0,117116	– 0,019157	0,003099		– 0,000487	0,000069
4	11,6	0,097959	– 0,016058	0,002613		– 0,000418	0,000065
5	12,5	0,081901	– 0,013445	0,002195		– 0,000353
6	13,4	0,068456	– 0,011250	0,001842
7	14,3	0,057206	– 0,009408
8	15,2	0,047798

2.	По формуле трапеций (7.26) находим
	0,247016		0,729642	0,767835 .
	I IТ 0,9	2	0,729642	0,767835 .
		2
3.	Аналогично проводим вычисления по формуле Симпсона (7.30):

233

IIС 03,9 (0,199218 4 0,167066 2 0,139938 4 0,117116 2 0,097959

4 0,081901 2 0,068456 4 0,057206 0,047798) 0,765865.

4.Оценим погрешности вычислений. Погрешность округления

* (b a) 0 3,6 10 6
(значения функции f (x) вычислены с ошибкой 0	0,5 10 6 , так как округления

производились в шестом знаке после запятой). Оценку погрешностей методов проводим по формулам (7.42) и (7.43). Так как max | 2 y | 0,005024 , то для метода трапеций

		[8;15,2]
		Т 0,005024		15,2 8 0,0030144
				12
и	полная погрешность Т	Т * 0,003018 0,003. Следовательно,				IТ 0,768 0,003 .
Соответственно для метода Симпсона имеем
	max \| 4 y \| 0,000079,		С	0,000079 15,2 8	0,0000032
	[8;15,2]			180
и	С С * 0,0000068.	Поэтому	IС	0,765865 0,000007. Таким		образом, метод

Симпсона дает значительно более точный результат, чем метод трапеций.

5. Продолжаем выполнение работы в компьютерном классе. Запускаем программу Mathcad. Открываем файл Lab3.mcd. Вводим функцию

f (x) : atan(e 5 ) ,

а также нижний и верхний пределы интегрирования a : 8, b : 15.2.

Программа автоматически строит график подынтегральной функции f (x) на отрезке [a, b]

(рис. 7.14).

Рис. 7.14.

Согласно геометрическому смыслу определенного интеграла необходимо вычислить площадь криволинейной трапеции (серая область на рис. 7.14).

Программа автоматически вычисляет интеграл с точностью до 10 10 :

I : f (x)dx, I 0.7658625496

6. Записываем полученное на компьютере решение

IК 0,7658625496

и вычисляем абсолютные погрешности, с какими найдены с помощью МК значения интеграла по методу трапеций и Симпсона:

234

Т | IК IТ | | 0,7658625496 0,767835| 0,002;

С | IК IС | | 0,7658625496 0,765865 | 0,000003.

7.Используя формулы (7.44), программа в конце пункта «Метод правых прямоугольников» вычисляет число точек разбиения отрезка интегрирования [a, b],

обеспечивающее точность 1 10 4 методов левых и правых прямоугольников:

n nПП nЛП 10057 .

Подставляя n 10057 в начало пункта «Метод левых прямоугольников» программы,

записываем решение
I КПП 0,765808,	IКЛП 0,765917,
с абсолютными погрешностями

| I IКПП | | 0,7658625496 0,765808 | 5,42 10 5 ,

| I IКЛП | | 0,7658625496 0,765917 | 5,42 10 5.

8. Используя формулу (7.45), программа в конце пункта «Метод средних прямоугольников» вычисляет число точек разбиения отрезка интегрирования [a, b],

обеспечивающее точность 2 10 6 метода средних прямоугольников:

n nП 334 .

Подставляя n 334 в начало пункта «Метод средних прямоугольников» программы, записываем решение

IКП 0,76586198,

с абсолютной погрешностью

| I IКП | | 0,7658625496 0,76586198 | 5,66 10 7.

9. Используя формулу (7.46), программа в конце пункта «Метод трапеций» вычисляет число точек разбиения отрезка интегрирования [a,b], обеспечивающее точность 2 10 6 метода трапеций:

n nТ 472 .

Подставляя n 472 в начало пункта «Метод трапеций» программы, записываем решение

I КТ 0,76586312,

с абсолютной погрешностью

| I IКТ | | 0,7658625496 0,76586312 | 5,67 10 7.

10. Используя формулу (7.47), программа в конце пункта «Метод Симпсона» вычисляет число точек разбиения отрезка интегрирования [a, b], обеспечивающее точность 2 10 6 метода Симпсона. Получим nС 11 . Следовательно, так как n должно быть четным,

подставляем n 12 в начало пункта «Метод Симпсона» программы. Записываем решение

I КС 0,76586306,

с абсолютной погрешностью

| I IКТ | | 0,7658625496 0,76586306 | 5,14 10 7. 11. Все расчеты оформляются в виде отчета по лабораторной работе.

235

7.3.9. Основные термины

Первообразная Неопределенный интеграл Интегральная сумма Определенный интеграл Формула Ньютона-Лейбница Криволинейная трапеция Элементарная трапеция Шаг интегрирования Метод прямоугольников Метод трапеций Метод Симпсона Конечные разности Метод Рунге

7.3.10.Вопросы для самоконтроля

1.Дайте определение определенного интеграла.

2.Дайте определение неопределенного интеграла.

3.Что такое первообразная для функции?

4.Приведите формулу Ньютона-Лейбница.

5.В каких случаях целесообразно использовать формулы численного интегрирования?

6.Используя геометрическую интерпретацию, выведите формулы левых и правых прямоугольников.

7.Приведите оценку погрешности формул левых и правых прямоугольников.

8.Выведите формулу средних прямоугольников.

9.Приведите оценку погрешности формулы средних прямоугольников.

10.Выведите формулу трапеций.

11.Приведите оценку погрешности формулы трапеций.

12.Выведите формулу Симпсона.

13.Приведите оценку погрешности формулы Симпсона.

14.Получите формулу выбора начального шага в формуле трапеций.

15.Получите формулу выбора начального шага в формуле Симпсона.

16.В чем состоит правило Рунге оценки погрешностей? Получите оценки погрешностей формул трапеций и Симпсона по правилу Рунге.

17.Как находится полная погрешность вычисления определенного интеграла?

236

7.4. Численное интегрирование обыкновенных дифференциальных уравнений первого порядка

7.4.1. Постановка задачи

Многие практические задачи при их математическом моделировании сводятся к решению обыкновенных дифференциальных уравнений, т. е. к уравнениям, в которые входят независимая переменная, искомая функция и ее производные. В данной лабораторной работе рассматриваются численные методы поиска решения y(x) для дифференциального

уравнения первого порядка
y f (x, y),	(7.50)
которое удовлетворяет начальному условию
y(x0 ) y0 .	(7.51)

Известно [6]–[8], что для существования и единственности решения этой задачи

(задачи Коши) достаточно, чтобы функция f (x, y) и ее частная производная fy были

непрерывны в некоторой области плоскости Oxy , содержащей окрестность точки M 0 (x0 , y0 ) . В то же время аналитическое решение задачи Коши можно найти только в

отдельных, наиболее простых случаях, изучаемых в курсе высшей математики [6]. В остальных случаях решение ищется приближенными методами.

Все приближенные методы в зависимости от формы, в которой они представляют решение, можно условно разделить на следующие группы: аналитические (дают приближение y(x) аналитическим выражением), графические (дают приближение y(x)

графиком) и численные (дают приближение y(x) с помощью таблицы). В данной

лабораторной работе рассматриваются лишь два из большого числа численных методов решения задачи Коши: метод Эйлера и метод Рунге-Кутта [6]–[8]. При этом решение

y y(x) находится в виде таблицы значений: y0 , y1, y2 ,..., yn соответственно для значений аргумента: x0 , x1, x2 ,..., xn .

Рис. 7.15.

Если соединить найденные в процессе решения точки (x0 , y0 ), (x1, y1), (x2 , y2 ),..., (xn , yn )

гладкой кривой, то получим график приближенного решения задачи Коши (на рис. 7.15: кривая 1 – интегральная кривая y=y(x); кривая 2 – график приближенного решения задачи

Коши ). Этот график по мере удаления от начальной точки (x0 , y0 ) все более и более будет

отклоняться от графика точного решения (интегральной кривой). Степень отклонения приближенного решения от точного характеризует точность численного метода.

237

7.4.2. Метод Эйлера

Метод Эйлера состоит в следующем. Отрезок [a,b], на котором ищется приближенное решение, делится точками

a x0 , x1 x0 h, x2 x0 2h,..., xn x0 nh b

на n равных частей, где h b a – шаг интегрирования дифференциального уравнения. Зная n

значение y0 решения y y(x) в точке x0 , можно найти приближенно		y(xi 1) yi 1 в точках
xi 1 xi h по следующей рекуррентной формуле:
yi 1 yi hf (xi , yi ),	i 0,1,..., n 1.		(7.52)
Геометрически в методе Эйлера искомую интегральную кривую на интервале (x0 , x1)
заменяем отрезком касательной к этой интегральной кривой в точке			M 0 (на рис. 7.16:
1 – искомая интегральная кривая, 2,3 – другие интегральные кривые).

Рис. 7.16.

Уравнение касательной имеет вид

y y(x0 ) y (x0 ) (x x0 ),

где y(x0 ) y0 , y (x0 ) f (x0 , y0 ), x x1, y y1, x x0 h . Поэтому ордината касательной в точке x1 равна y1 y0 h f (x0 , y0 ) , т. е. получили формулу (7.52) для случая i 0 . Далее

строим касательную в точке M1 к интегральной кривой 2, которая уже не совпадает с искомой. Находим ординату y2 касательной в точке x2 , получаем формулу (7.52) уже при

i 1. И так до тех пор, пока не достигнем конца отрезка b (на рис. 7.17: 1 – ломаная Эйлера, 2 – искомая интегральная кривая).

Рис. 7.17.

Для оценки локальной погрешности метода Эйлера в точке xi используется неравенство [6]–[8]

	Э	\| y* y(x		) \| \| y* y	i	\|,	(7.53)
	Э	i	i	i	i

238

где	y(x )	–	точное значение решения задачи Коши в точке x ,	а y	, y* – приближенные
	i		i	i		i
значения решения, вычисленные по формуле (7.52) с шагами h				и h / 2		соответственно. Из
неравенства (7.53) следует, что для достижения необходимой точности						нужно просчитать
значение		y	по формуле (7.52) с шагом h , а затем, уменьшив шаг вдвое, снова повторить
расчеты.		Если при этом окажется, что для всех i 1,2,..., n		выполняется неравенство
\| y* y \| ,			то на шаге h достигнута необходимая точность.
i	i

7.4.3. Метод Рунге-Кутта

Метод Эйлера прост в реализации, но обладает сравнительно небольшой точностью. Поэтому для решения задачи Коши с повышенной точностью обычно используют метод Рунге-Кутта [6]–[8].

Как и прежде, разбиваем отрезок интегрирования [a,b] на n равных частей. Зная значения yi – решение задачи Коши в точке xi , будем искать значение решения в точке xi 1 по следующей формуле Рунге-Кутта:

yi 1 yi K0 2K1 2K2 K3 ,		(7.54)
где	6
где
K0	h f (xi , yi );
K1	h f (xi 0,5 h, yi 0,5 K0 );	(7.55)
K2	h f (xi 0,5 h, yi 0,5 K1);	(7.55)
K2	h f (xi 0,5 h, yi 0,5 K1);

K3 h f (xi h, yi K2 ).

Вычисления по формулам (7.54), (7.55) выполняются в следующем порядке. Для

начальной точки (x0 , y0 ) , где x0 a , вычисляют K0 , затем последовательно K1, K2						и	K3 .
После	этого		все значения подставляются в формулу (7.54) (i 0) и находится			y1	при
x1 x0	h . Далее процесс продолжается аналогично до конца отрезка b .
Для оценки локальной погрешности метода Рунге-Кутта используется неравенство
[7], [8]:				1
			Р К \| yi* y(xi ) \|	1	\| yi* yi \|,	(7.56)
			Р К \| yi* y(xi ) \|		\| yi* yi \|,	(7.56)
			15
где y(x ), y		,	y* имеют тот же смысл, что и в неравенстве (7.53).
	i i		i

7.4.4. Выбор шага интегрирования

Точность методов Эйлера и Рунге-Кутта существенно зависит от величины шага интегрирования h. Можно доказать [7], [8], что погрешность метода Эйлера имеет порядок h,

а метода Рунге-Кутта – порядок h4 . Т. е. для достижения одной и той же точности в методе Эйлера нужно выбрать гораздо меньший шаг интегрирования, чем в методе Рунге-Кутта.

Рассмотрим подробнее процедуру выбора и уточнения шага интегрирования на примере метода Рунге-Кутта. Пусть – заданная точность решения задачи Коши. Поскольку

Р К c h4 (где c=const), то начальное значение h0 можно выбрать из неравенства

h 4	.	(7.57)
0

При этом, чтобы попасть после n шагов интегрирования из точки a в точку b, необходимо выполнение условия:

n b a	N (натуральное число).	(7.58)
h
0

239

Кроме того, для подсчета погрешности метода Рунге-Кутта по формуле (7.56), нужно будет сделать просчет по формулам (7.54), (7.55) с шагом 2h. Поэтому необходимо также, чтобы

отношение (b a) / h0 было четным.

После выбора начального значения шага h h0 проводится его уточнение. Для этого из точки x0 a просчет по формулам (7.54), (7.55) выполняется дважды сначала с шагом h, а затем из той же точки с шагом 2h. При этом получаются два значения решения задачи ( y2 и y2* ) в одной и той же точке x 2h . Если | y2 y2* | , то h0 можно выбрать в качестве шага интегрирования, иначе необходимо уменьшить h в два раза и повторить процедуру проверки.

7.4.5. Задание на лабораторную работу

1.	Из табл. 7.12 выбрать свой вариант задания ( y f (x, y), x [a,b], y0																											y(a) ).
															Варианты заданий												Таблица 7.12
															Варианты заданий
№			f (x, y)											a	b	y(a)	№	f (x, y)									a	b	y(a)
									y														y
1		x sin												1	3,4	2	16	y sin									2	2,8	1
1		x sin												1	3,4	2	16	y sin									2	2,8	1
									x														x
2				x e y										3	3,8	4	17	xy y									2	4,4	3
3			x							y				0	1,6	2	18	y				sin x					3	3,8	1
3			x				ln y							0	1,6	2	18	y									3	3,8	1
							ln y																y
4				1						y				0	3,2	1	19	x cos							y		1	2,6	2
4										y				0	3,2	1	19	x cos									1	2,6	2
			x y																				x
5	y			x							cos y			1	1,8	1	20	y cos							y		3	5,4	1
																		y cos

																							x
6			x	1								x		3	5,4	2	21		x y								2	3,6	2
6			x	1										3	5,4	2	21		x y								2	3,6	2
													y						x y
7			e xy						y					2	5,2	1	22	y e x y									1	3,4	2
8				y x2										1	1,8	4	23	x e y x									3	3,8	1
			x			sin y																		x
9														0	1,6	1	24	x cos									2	5,2	1
																		x cos
										y
										y										x y
												y														x
10			y									y		4	6,4	0.5	25	1 cos								x	3	4,6	1
												x														y
												x														y
11	y ln(y x)													0	1,6	2	26	y2 x2									2	2,8	3
12			y e y / x											3	4,6	0	27	y					x				4	4,8	1
12			y e y / x											3	4,6	0	27	y			ln(x)						4	4,8	1
																					ln(x)
																							x
13				y	2				x					1	1,8	2	28	ln					x				1	2,6	1
					2													ln
																							y
																		x					y
			ln x																				y
14				x				y						4	5,6	3	29	x sin									2	2,8	1
14								y						4	5,6	3	29	x sin									2	2,8	1
																							x
15			y						1					3	4,6	1	30	cos(x y)									0,6	2,2	0
15			y			x y								3	4,6	1	30				x						0,6	2,2	0
						x y															x

240

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 2324 / 2824 25 26 27 28 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.02.201581.23 Кб168.docx
#
20.09.2019105.47 Кб18_beR.doc
#
07.02.2015282.72 Кб399-105.docx
#
06.02.2015219.14 Кб17Abl_BH_Met_Flash.doc
#
06.02.201526.62 Кб14about_myself_1.doc
#
07.02.20152.14 Mб36Ankilov.pdf
#
18.11.2019159.23 Кб3Arkhivovedenie-1.doc
#
13.08.2019157.18 Кб3B7.doc
#
20.12.2018451.58 Кб21Batychko_V_T_Trudovoe_pravo_v_voprosah_i_otveta....doc
#
26.04.2019304.13 Кб2bilety_po_yazykoznaniyu_Vosstanovlen.doc
#
05.08.201967.37 Кб2Bilet_ps.docx