Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ульяновский Государственный Педагогический Университет им. И. Н. Ульянова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ankilov

.pdf

Скачиваний:

Добавлен:

07.02.2015

Размер:

2.14 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2810 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

б) поверхности интегрирования S;

в) выбора стороны поверхности интегрирования.

7. Если S – часть плоскости х + у + z = 1, лежащая в первом октанте, то поверхностный интеграл d равен:

	а)	3 / 3 ;
	б)	3 / 2 ;
	в)	2 / 2 ;
	г)	3 ;
	д)	2 / 3 .		cos ,cos ,cos – ее
8.	Если V – объем тела, ограниченного поверхностью S, а
8.	Если V – объем тела, ограниченного поверхностью S, а		n
внутренняя нормаль, то поверхностный интеграл (x cos y cos z cos )d равен:
		S
	а)	0;
	б)	V;
	в) – 2 V;
	г) – 3 V;
	д) 3 V.
9.	Если линия С задана уравнениями x cost, y sin t, z sin t (0 t 2 ) , то

криволинейный интеграл sin y dx x cos y dy z dz равен:

а) 2π; б) π; в) 1; г) 2; д) 0.

10.Если S – внешняя сторона сферы (х – 1)2 + у2 + z2 = 4, то поверхностный интеграл

2x dy dz ez dx dz z dx dy равен:

а) 12π; б) 32; в) 24π; г) 32π; д) 0.

3.6.2. Задачи Образцы решения задач

Задача 1.1. Вычислить криволинейный интеграл первого рода

	ds	;	C : x et (cost sin t),	y et (cost sin t),	3 t 2 .
	x y
C

Решение. Так как линия интегрирования С задана параметрически, то для вычисления интеграла воспользуемся формулой (3.4)

f (x, y)ds f [x(t), y(t)] (xt )2 ( yt )2 dt .

В данном случае 3, 2 ,

xt et

(cos t sin t) et ( sin t cos t) 2et cos t,

следовательно,

yt et

(cost sin t) et ( sin t cos t) 2et sin t,

/ 2

4e2t cos2

t 4e2t

sin 2 t

/ 2 2et dt

/ 2

ln tg

/ 2

/ 3

x y

et (cost sin t) et (cost sin t)

2et sin t

sin t

/ 3

ln tg

ln1 ln

1 ln 3.

Задача 1.2. Вычислить криволинейный интеграл первого рода

(x 2 y )ds;

C : y x2 , 1 x 1.

Решение. Имеем yx 2x,

1 ( yx )2

1 4x2 . Применяя формулу (3.5)

f (x, y)ds f [x, y(x)] 1 ( yx )2 dx ,

получим

(x 2 y )ds

(x 2

x2 ) 1 4x2 dx (x

2 | x |) 1 4x2 dx

d(1 4x

)

1 4x

d(1

)

3 x 1 4x

x 1

53 2

53 2 1.

(1 4x2 )3 2

2 (1 4x2 )3 2

8 3

Задача 2.1. Найти работу силы

при перемещении материальной

(x y)i

(x y) j

точки вдоль верхней половины эллипса

1 от точки А (а, 0) к точке В (–а, 0).

Решение.

Работа

силы

{P(x, y), Q(x, y)}

выражается

интегралом

P(x, y)dx Q(x, y)dy , который в данном случае удобно вычислить по формуле (3.11),

используя параметрическое представление эллипса: x a cos t, y bsin t . Верхней половине эллипса соответствует изменение параметра t от 0 до π. Таким образом, имеем

																	(a cos t bsin t)b cos t dt
W (x y)dx (x y)dy (a cos t bsin t)( a sin t)																	(a cos t bsin t)b cos t dt
AB						0

		( a2			cos t sin t absin 2 t ab cos2								t b2				sin t cost)dt
		0
			2	a	2				b	2	a	2


	b												cos 2t									ab.
				2		sin 2t ab dt					4		cos 2t				abt					ab.
	0			2							4										0
Задача 2.2.	0															x2					0

	Найти					работу силы		F (xy x)i											j	вдоль			линии		С, заданной
	Найти					работу силы		F (xy x)i									2		j	вдоль			линии		С, заданной
																	2
уравнением y 2	x , от точки А (0, 0) к точке В (1, 2).
Решение. Применяя формулу (3.12), получим																									1
	x2			1			x2		1				1 5 3 2										5 2 x2				1 1
	x2			1			x2		1				1 5 3 2										5 2 x2				1 1
W (xy x)dx		dy (x 2 x x)									dx				x											1
																													.
	2						2		x					2				x dx x						2			2	2	.
AB	2			0			2		x				0	2										2	0		2	2
																									0

Задача 3. С помощью формулы Грина вычислить интеграл

xydx x2 dy ,

где С –

замкнутый контур, состоящий из частей кривых

y 1 x2 , y 0 . Направление

обхода

контура С – положительное.

Решение. Формула Грина имеет вид

P(x, y)dx Q(x, y)dy

Q P

dxdy ,

где D – область, ограниченная контуром С.

В данном случае P(x, y) xy,

Q(x, y) x2 , Q

2x,

x , следовательно,

xydx x2 dy xdxdy .

Область D ограничена снизу прямой у = 0, сверху – параболой у = 1 – х2 ( 1 х 1) ,

поэтому

1 x2

xydx x

xdxdy dx xdy

x(1 x

0 .

)dx

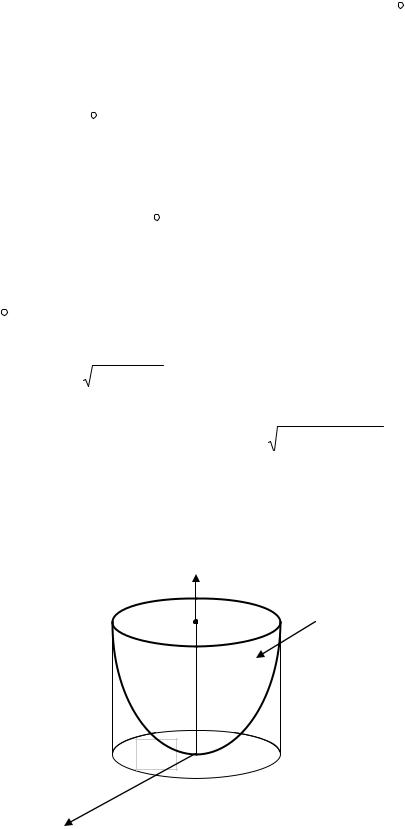
Задача 4. Вычислить поверхностный интеграл первого рода

z 1 x2 y 2 d ;

S : z

(x2 y 2 ) (0 z 2) .

Решение. Для вычисления интеграла воспользуемся формулой (3.25).

f (x, y, z)d f [x, y, z(x, y)]

1 (zx )2

(z y )2 dxdy ,

где D – проекция поверхности S на плоскость Оху.

В данном случае поверхностью интегрирования S является часть параболоида вращения z 12 (x2 y 2 ) , отсеченная плоскостью z = 2 (рис. 3.17), а область D ограничена окружностью х2 + y2 = 4.

z
2	z	1	(x2	y 2 )
2		2

D у

x2 y 2 4

Рис. 3.17

Уравнение окружности получается из уравнения параболоида при z = 2. С учетом того, что zx x , z y y , будем иметь

z	1 x2 y2 d 1	(x2	y2 )	1 x2 y2	1 x2 y2 dxdy	1	(x2 y2 )(1 x2 y2 )dxdy.
D	D 2					2	D

Переходя в полученном двойном интеграле к полярным координатам по формулам x r sin , y r sin , находим

z 1 x	2	y		2	d				1		2				2			2		(1 r			2	)rdr				1		2		2		3		r		5	)dr
z 1 x		y			d				2			d r								(1 r				)rdr				2		d (r						r			)dr
S									2			0			0													2		0		0
			2			4					6				2
			2			4					6				2
		1								r											1				32							44
		1		r						r						d					1		4		32			2				44				.

		2				4				6											2				3								3
		2	0			4				6											2				3								3
															0
															0
Задача 5. Вычислить поверхностный интеграл второго рода
						xdydz y 2z dxdz z 2 y dxdy,
						S																			z 0 .
где S – верхняя сторона полусферы: x2															y 2				z 2			4			z 0 .
Решение. Воспользуемся формулой (3.33)																																			Q dxdy
Pdydz Qdxdz Rdxdy R zx P z y																																			Q dxdy
S																								D
со знаком «+», т. к. нормаль к выбранной стороне поверхности																																	S				образует острый угол с
осью Oz . Для полусферы S :																						x																y
z	4 x2 y2 ,												zx									x					, z y											y			,
z	4 x2 y2 ,												zx							4 x2 y2							, z y														,
																				4 x2 y2														4 x2 y2
поэтому		I xdydz y 2z dxdz z 2 y dxdy
		I xdydz y 2z dxdz z 2 y dxdy
					S
								x	2								y			2	2 y			4 x				2		y	2										dxdy
4 x2 y 2	2 y							x									y				2 y			4 x						y		dxdy 4									dxdy				.
4 x2 y 2	2 y								2						2										2				2			dxdy 4										2		2	.
					4 x				2	y					2							4 x			2	y			2											4 x		2	y	2
D					4 x					y												4 x				y													D	4 x			y
Поскольку D (проекция S на плоскость																						Oxy ) есть круг, то, переходя к полярным
координатам, окончательно будем иметь:
					dxdy											2					2		rdr														2	2
																2					2																	2
I 4														4 d													8					4 r							16 .
I 4			4 x				2	y				2		4 d									4 r			2	8					4 r						0	16 .
	D		4 x					y								0					0		4 r															0

Расчетное задание

Задача 1. Вычислить криволинейный интеграл первого рода.

1. 3		y 43 x ds; C : y x 1, 1 x 0.
	С		C : x a t sin t , y a 1 cost , 0 t 2 .
2.	yds;		C : x a t sin t , y a 1 cost , 0 t 2 .
	C
3.			ds		; C : y 2x, 0 x 1.
3.		x2			; C : y 2x, 0 x 1.
	C	x2	y 2 4
4.	x2 y 2 ds;			C : x a cost t sin t , y a sin t t cos t ,				0 t 2 .
	C
5. 2x y ds; C : y 1						x	, 1 x 1.
5. 2x y ds; C : y 1						x	, 1 x 1.
	C
6. xy2 ds; C : x a cos t, y a sin t, 0 t 2.
	C

yds;

C : y a ch

0 x a.

C:x acost, y bsint, 0 t 2 .

ds;

yds;

C : y

2x, 0 x 1.

10.

y 2 ds;

C : x a ch t, y a sh t, 0 t 1.

Задача 2. Найти работу силы

при перемещении материальной точки вдоль линии С

от точки А к точке В.

2 y i

y 2

; C : отрезок АВ, А(–4, 0), В(0, 2).

x3i

C : x2

y 2 4 x 0, y 0 , А(2, 0), В(0, 2).

;

2 y i

y 2

; C : y 2

, А(–4, 0), В(0, 2).

x y i

x y

; C : x2

y 2

1 x 0, y 0 , А(1, 0), В(0, 3).

x2 yi

;

C : отрезок АВ, А(–1, 0), В(0, 1).

x y i

; C : x2

y 2 4 y 0 , А(2, 0), В(–2, 0).

2xj

xy y 2 i

C : y 2x2 ,

;

А(0, 0), В(1, 2).

y 2 i

y 2

; C :

y 2

1( y 0), А(3, 0), В(–3, 0).

; C : y x3 ,

А(0, 0), В(2, 8).

10.

; C : x2

y 2

9 x 0, y 0 , А(3, 0), В(0, 3).

Задача 3. С помощью формулы Грина вычислить интеграл (направление обхода

контура С – положительное).

1. x2 y dx y 2 2x dy;

C : y x2 1, y 2.

2. x2 y 2 dx x2 y 2 dy; C : y

a2 x2 , y 0.

dx 2 ln xdx;

C : 2x y 4, x 1, y 0.

x y 2 dx x y 2 dy;

C : y sin x, y 0, 0 x .

dx2 dy

; C : y x, x 2, y 1.

x2 ydx xy2 dy;

C : x2 y 2 a2 .

7. x y 2 dx x2 y 2 dy; C : y 0, x 0, x y 1.

ex 1 cos y dx ex 1 sin y dy; C : y 0, x 1, y x.

9. x y3 dx y x3 dy; C : x2 y 2 a2 .

C
10. xy2 dx x2 ydy; C : y 2 x, y x2 .
C
Задача 4. Вычислить поверхностный интеграл первого рода.
1. yzd ;			S : x y z 1 x 0, y 0, z 0 .
S
2. x z d ; S : x2 y 2 z 2 a2 z 0 .
S
3.	x2 y 2 d ; S : x2 y 2 z 2 0 z 1 .
S
4.	d				; S : x y z 1 x 0, y 0, z 0 .
4.	1 x y			2	; S : x y z 1 x 0, y 0, z 0 .
S	1 x y
5.	x2 y 2 z 2 d ; S : x2 y 2 z 2 1 z 0 .
S
6.	d	; S : z 1 x2 y 2 0 z 1 .
6.	1 2z	; S : z 1 x2 y 2 0 z 1 .
S	1 2z			2
7. xd ; S : z 1 x2 y 2 .
S
8. z 2 d ; S : x2 y 2 z 2 0 z a .
S
9. 1 4x2 4 y 2 d ; S : z 1 x2 y 2 0 z 1 .
S
10. x y d ; S : x y z a x 0, y 0, z 0 .
S

Задача 5. Вычислить интеграл Pdydz Qdxdz Rdxdy, где S – часть поверхности S1,

отсеченная плоскостью Р (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями).

1. x xy2 dydz y yx2 dxdz z 3 dxdy;				6.	x y dydz y x dxdz zdxdy;
	S				S
	S1	: x2 y 2 z 2 z 0 , P : z 1.			S1 : x2 y 2 z 2 4, P : z 0 z 0 .
2.				7.		y 2 xdydz yx2 dxdz dxdy;
2.		xdydz y z dxdz z y dxdy;		7.		y 2 xdydz yx2 dxdz dxdy;
	S				S
	S1 : x2 y 2 z 2 9, P : z 0 z 0 .				S1 : x2 y 2 z 2 z 0 , P : z 5.
3. xydydz x2 dxdz 3dxdy;				8.	x y dydz x y dxdz zdxdy;
	S				S
	S				S1 : x2 y 2 z 2 1, P : z 0 z 0 .
	S1 : x2 y 2 z 2 z 0 , P : z 1.				S1 : x2 y 2 z 2 1, P : z 0 z 0 .
4. x xy2 dydz y yx2 dxdz zdxdy;				9.	xyzdydz x2 zdxdz 3dxdy;
	S				S
	S1 : x2 y 2 z 2 9, P : z 0 z 0 .				S1 : x2 y 2 z 2 z 0 , P : z 2.
5. xzdydz yzdxdz z 2			1 dxdy;	10. xdydz y yz dxdz z y 2 dxdy;
	S				S
	S				S1 : x2 y 2 z 2 1, P : z 0 z 0 .
	S1 : x2 y 2 z 2 z 0 , P : z 4.				S1 : x2 y 2 z 2 1, P : z 0 z 0 .

ГЛАВА 4. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ

Понятие поля лежит в основе многих представлений современной физики.

В общем случае говорят, что в пространстве задано поле некоторой величины u, если в каждой точке пространства (или некоторой его части) определено значение этой величины. Так, например, при изучении потока газа приходится исследовать несколько полей: температурное поле (в каждой точке температура имеет определенное значение), поле давлений, поле скоростей и т. д.

Поле величины u называется стационарным, если u не зависит от времени t. В противном случае поле называется нестационарным. Таким образом, величина u есть функция точки М и времени t.

В физических задачах приходится иметь дело как со скалярными, так и с векторными величинами. В соответствии с этим различают два вида полей: скалярное и векторное. Для простоты будем считать их стационарными.

4.1.Скалярное поле. Производная по направлению

иградиент скалярного поля

Пусть D – область на плоскости или в пространстве. Говорят, что в области D задано скалярное поле, если в D задана скалярная функция z f x, y ( u f x, y, z ). Если,

например, область D заполнена жидкостью или газом, и f x, y, z обозначает температуру в точке М(x,y,z), то говорят, что задано скалярное поле температур; если f x, y, z – давление,

то задано скалярное поле давлений и т. д. Важнейшими характеристиками скалярного поля являются производная по направлению и градиент.

Рассмотрим функциюz f x, y , определенную в некоторой окрестности точки М(х,у),

и произвольный векторs , выходящий из точки М (рис. 4.1). Для характеристики изменения функции (поля) в

точке М (х,у) в направлении вектора s введем понятие производной по направлению. Для этого через точку М

проведем прямую			L	в направлении	вектора	s .	На
прямой L		возьмем		точку М1(х +	х, у +	у)	на
расстоянии		s	от	точки М. Таким образом,
s	x 2	y 2 .		Функция z f (x, y) получит при
этом приращение

z f x x, y y f x, y .

s L

М1

уМ β α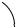

О х х+ х

Рис. 4.1

Определение 4.1.1. Предел отношения				z	при s→0, если он существует, называется
				s
производной функции (скалярного поля) z f x, y в точке М (х,у) по направлению вектора s
и обозначается	z	, т. е.
	s	z			z .
		z	lim		z .
		s		s 0	s

Производная zs – скорость изменения функции (скалярного поля) вдоль выбранного направления.

Предположим теперь, что функция z = f(x,y) дифференцируема в точке М(х,у). Тогда ее полное приращение в этой точке в направлении вектора s можно записать в виде

z f x x, y x f y x, y y 1 x 1 y ,

где α1 и β1 – бесконечно малые функции при s→0. Разделим обе части этого равенства на s. Учитывая, что x s cos , y s cos (рис. 4.1), получим

z	f x x, y cos f y x, y cos 1 cos 1 cos .
s
Переходя к пределу при s→0, получаем формулу для производной по направлению
	z	z cos	z	cos .		(4.1)
	s	z cos		cos .		(4.1)
	s	x	y
Из формулы (4.1)	следует, что производная по				направлению вектора s	является
линейной комбинацией	частных производных,		причем		направляющие косинусы	вектора

s (cos α, cos β) играют роль весовых множителей, показывающих вклад в производную по направлению соответствующей частной производной.

В частности,

при α = 0,

;

при

, β = 0. Отсюда следует,

что частные производные

–

производные

направлении осей Ох и Оу

соответственно.

Пример 4.1.2. Вычислить производную скалярного поля z=x2+y2x в точке М (1,2) по направлению вектора s MN , где N – точка с координатами (3,0).

Решение. Найдем направляющие косинусы вектора													MN		:	MN	{2, 2} 2i 2					j	;
		22 2 2	8 2	2 , cos						2		1		, cos				2		1	.
	MN									2		1						2		1
	MN
									2	2		2		2					2	2
									2	2		2		2					2	2
Вычислим частные производные функции в точке											М:			f x x, y 2x y 2 ,						f y x, y 2 yx ,
откуда f x 1,2 6 ,		f y 1,2 4 . По формуле (4.1)					получим
		z	6	1	4	1		2			1	2 .
		s	6	2	4	2		2			2	2 .
		s		2		2					2
Определение 4.1.2. Градиентом функции (скалярного поля) z = f(x,y)																				в точке М(х,у)

называется вектор, координаты которого равны соответствующим частным производным

z .

Обозначение: grad z

z i

j .

Используя формулу (4.1)

учитывая,

что

{

cos ,

cos }, найдем скалярное

произведение векторов grad z и s :

grad z,

cos

z .

(4.2)

С другой стороны, по определению скалярного произведения имеем

grad z,

grad z

cos ,

(4.3)

где φ – угол между векторами s

и grad z. Сравнивая формулы (4.2) и (4.3), получаем

grad z

cos .

(4.4)

Из равенства (4.4) следует, что производная функции по направлению имеет

наибольшую величину при cos φ=1 (φ=0), т. е. когда направление вектора

совпадает с

направлением grad z. При этом

grad z

zx 2

z y 2 .

Таким образом, градиент функции z = f(x,y) в точке М(х,у) характеризует направление и

величину наибольшей скорости возрастания этой функции в данной точке.

Аналогично определяются производная

по направлению вектора

для функции

трех переменных u = f(x,y,z) и выводится формула

u cos u cos u cos ,

где cos α, cos β, cos γ – направляющие косинусы вектора s . Градиентом функции u = f (x,y,z)

называется вектор	grad u	u	, u	,	u . Связь между градиентом и производной по
		x	y
		x	y		z

направлению устанавливается формулой					, grad u),
u	grad u	cos ,	(
u	grad u	cos ,	(	s
s
s

вывод которой аналогичен выводу формулы (4.4).

Аналогичным образом определяются градиент и производная по направлению и для функции n переменных (n – мерного скалярного поля, n 3).

4.2.Векторное поле

4.2.1.Понятие векторного поля. Векторные линии

Аналогично с понятием скалярного поля вводится понятие векторного поля. Говорят, что в плоской или пространственной области D задано векторное поле, если в D задана

векторная функция a a (M ), т. е. каждой точке М из D поставлен в соответствие вектор a.

Примеры векторных полей:

1. В пространстве, окружающем Землю, существует гравитационное векторное поле: на материальную точку, внесенную в любую точку М указанного пространства, действует

сила тяжести P (M ).

2.Вокруг тела, заряженного электричеством, наблюдается векторное поле напряженности, которое проявляется при внесении в любую точку пространства, окружающего тело, заряженной частицы.

3.Пусть некоторая пространственная область D занята текущей жидкостью. Если любая частица жидкости, протекая через данную точку М области D, имеет один и тот же

вектор скорости a (М), то в области D имеет место гидродинамическое поле a (М)

скоростей текущей жидкости.

Если в пространственной области D введена система координат Oxyz, то задание пространственного векторного поля a a (M ) равносильно заданию трех скалярных

функций P (x, y, z), Q (x, y, z), R (x, y, z), являющихся проекциями вектора a (М) на оси координат:

a (M ) P (x, y, z) i Q (x, y, z) j R (x, y, z) k.

Здесь x, y, z – координаты точки M D.

Если векторное поле a a (M ) плоское (D – область на плоскости Oxy), то

a (M ) P (x, y) i Q (x, y) j.

Пример 4.2.1. Найти векторное поле напряженности, создаваемое точечным положительным зарядом величиной q.

Решение. В пространстве зафиксируем систему координат Oxyz и поместим заряд в точку О.

В каждой точке M (x, y, z) пространства на единичный положительный заряд действует отталкивающая сила E , которая называется напряженностью электростатического поля.

Вектор

направлен вдоль линии, соединяющей заряды (рис. 4.2).

| q / r 2

x2 y2

z 2 – расстояние между

Согласно закону Кулона |

, где r

зарядами. Найдем проекции вектора

на координатные оси. Заметим, что векторы

x, y, z коллинеарны и сонаправлены,

следовательно,

где 0 . Отсюда

, а тогда E

x, y, z

– искомое векторное поле.

r 3

(M )

M (x, y, z)

Рис. 4.2

Рис. 4.3

Определение 4.2.1. Векторной линией

поля

(M ) называется

линия, в каждой

точке М которой направление касательной совпадает с направлением соответствующего вектора поля (рис. 4.3).

В силу этого определения вектор d r dx, dy, dz , направленный по касательной к

векторной линии поля a a (M ) в точке М, коллинеарен вектору a (M ) P, Q, R в

указанной точке. Условие коллинеарности этих двух векторов, которое записывается в форме

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2810 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.02.201581.23 Кб168.docx
#
20.09.2019105.47 Кб18_beR.doc
#
07.02.2015282.72 Кб399-105.docx
#
06.02.2015219.14 Кб17Abl_BH_Met_Flash.doc
#
06.02.201526.62 Кб14about_myself_1.doc
#
07.02.20152.14 Mб36Ankilov.pdf
#
18.11.2019159.23 Кб3Arkhivovedenie-1.doc
#
13.08.2019157.18 Кб3B7.doc
#
20.12.2018451.58 Кб21Batychko_V_T_Trudovoe_pravo_v_voprosah_i_otveta....doc
#
26.04.2019304.13 Кб2bilety_po_yazykoznaniyu_Vosstanovlen.doc
#
05.08.201967.37 Кб2Bilet_ps.docx