
Ankilov
.pdf
|
|
|
|
|
|
|
|
1 |
1 x |
1 |
|
|
8. |
Повторный (трехкратный) интеграл dx dy f (x, y, z)dz равен: |
|||||||||||
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
|
|
|
1 |
1 y |
x |
|
|
|
|
|
|
|
|
|
а) |
dy dx f (x, y, z)dz ; |
|
|
|
|
|
|||||
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
б) 1 dy 1 dz 1 |
f (x, y, z)dx ; |
|
|
|
|
|
|||||
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
в) 1 dy 1 dx1 |
f (x, y, z)dz ; |
|
|
|
|
|
|||||
|
|
0 |
1 y |
0 |
|
|
|
|
|
|
|
|
|
|
1 |
1 y |
1 x |
|
|
|
|
|
|
||
|
г) |
dx dz |
|
f (x, y, z)dy ; |
|
|
|
|
|
|||
|
|
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
1 |
1 y |
1 |
|
|
|
|
|
|
|
|
|
д) |
dy dx f (x, y, z)dz . |
|
|
|
|
|
|||||
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
9. |
Если |
область T ограничена поверхностями |
z |
x2 y2 , z 1, то, переходя в |
||||||||
тройном интеграле zdxdydz к цилиндрическим координатам r, , z , получим: |
||||||||||||
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
а) |
2 |
1 |
|
1 |
; |
|
|
|
|
|
|
|
d rdr zdz |
|
|
|
|
|
||||||
|
|
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
б) |
2 |
1 |
|
1 |
; |
|
|
|
|
|
|
|
d rdr zdz |
|
|
|
|
|
||||||
|
|
0 |
0 |
|
r |
|
|
|
|
|
|
|
|
|
2 |
1 |
|
1 |
|
|
|
|
|
|
|
|
в) |
d dr zdz ; |
|
|
|
|
|
|
||||
|
|
0 |
0 |
|
r |
|
|
|
|
|
|
|
|
г) |
2 |
1 |
|
|
1 |
; |
|
|
|
|
|
|
d r 2 dr dz |
|
|
|
|
|
||||||
|
|
0 |
0 |
|
|
r |
|
|
|
|
|
|
|
|
2 |
1 |
|
r |
|
|
|
|
|
|
|
|
д) |
d rdr zdz . |
|
|
|
|
|
|||||
|
|
0 |
0 |
|
0 |
|
|
|
|
|
|
|
10. |
Переходя |
|
в |
повторном интеграле |
a |
a2 x2 |
a2 x2 y2 |
к сферическим координатам |
||||
|
dx |
dy |
zdz |
|||||||||
, , , получим: |
|
|
|
0 |
|
0 |
0 |
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
а) |
d d 3 sin cos d ; |
|
|
|
|
|
|||||
|
|
0 |
0 |
|
0 |
|
|
|
|
|
|
|
б) 2 d 2 d a sin d ;
0 0 0
2 |
2 |
a |
в) d d 3 sin cos d ; |
||
0 |
0 |
0 |
|
2 |
2 |
a |
г) |
d d 2 cos d ; |
||
|
0 |
0 |
0 |
|
|
|
|
|
2 |
|
a |
д) |
d d 2 sin cos d . |
||
|
0 |
0 |
0 |
61
2.6.2. Задачи Образцы решения задач
Задача 1. Вычислить
|
|
|
|
|
|
|
|
|
|
(9x2 y 2 |
25x4 y 4 )dxdy; |
D : x 1, y |
x, y x2 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Строим область D (рис. 2.20). Для |
|||||||||||||||||||||||||||||||
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вычисления двойного интеграла в данном случае |
||||||||||||||||||||||||||||||||||||||
y x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
более удобной является формула (2.4) |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
2 ( x) |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x, y)dxdy dx |
f (x, y)dy. |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
O |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
1 ( x) |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
Если в повторном интеграле внешний |
|||||||||||||||||||||||||||||||||||||
y x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интеграл взять по у, а внутренний по х (см. |
||||||||||||||||||||||||||||||||||||||
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
формулу (2.5)), то область интегрирования |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
придется разбивать на две части, так как линию, |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Рис. 2.20 |
|
|
|
|
|
|
|
|
ограничивающую область D слева, нельзя |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
представить одним уравнением. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Найдем пределы интегрирования. Проекцией области D на ось Ох является отрезок |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[0,1]. Значит, |
a = 0, |
|
b = 1. Снизу |
область D |
ограничена |
|
параболой |
|
y x2 , |
|
сверху – |
||||||||||||||||||||||||||||||||||||||||||||||||
параболой y |
|
x , т. е. 1 (x) x2 , |
2 (x) |
|
x . Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
(9x |
2 |
y |
2 |
25x |
4 |
y |
4 |
|
|
|
1 |
x |
|
|
2 |
y |
2 |
|
25x |
4 |
y |
4 |
)dy |
1 |
|
|
|
2 |
|
y |
3 |
5x |
4 |
y |
5 |
|
x |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
)dxdy dx |
(9x |
|
|
|
|
|
|
3x |
|
|
|
|
|
|
x2 |
dx |
|
|||||||||||||||||||||||||||||||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
7 |
|
|
|
|
|
13 |
|
|
|
|
|
|
8 |
|
14 |
|
|
2 |
|
9 |
|
|
|
2 |
|
15 |
|
|
|
1 |
|
9 |
|
1 |
|
15 |
|
|
1 |
|
|
2 |
|
|
2 |
|
|
1 |
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
(3x |
2 |
5x |
2 |
3x |
5x |
)dx |
x |
2 |
x |
2 |
|
x |
|
x |
|
|
|
|
|
|
|
2. |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
3 |
|
|
3 |
|
3 |
|
|
|
|
|
3 |
|
3 |
3 |
3 |
|||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Задача 2. Найти площадь фигуры, ограниченной линиями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
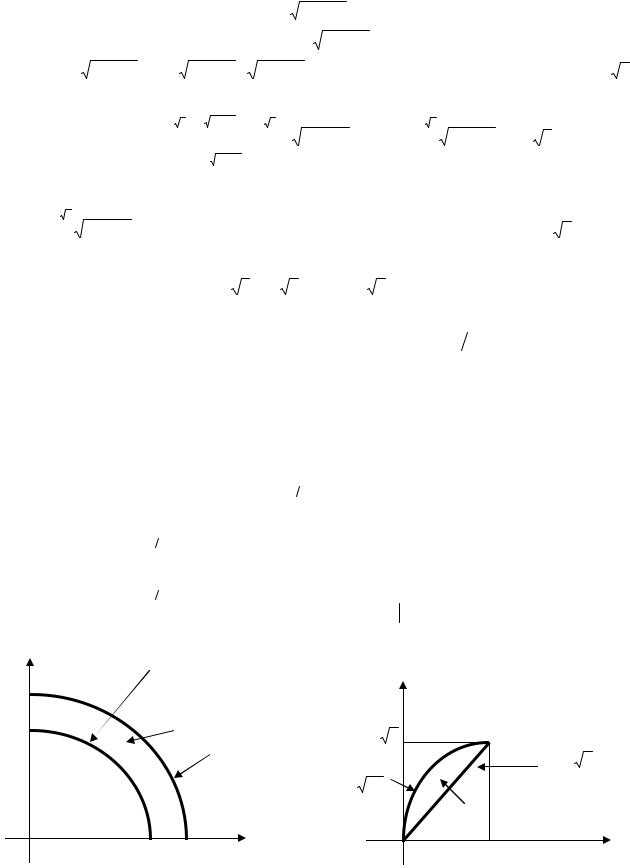
y 16 x2 , y 4 16 x2 , x 0 (x 0). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Решение. |
|
|
|
Преобразуем |
|
уравнение |
|
|
|
|
|
|
первой |
|
|
|
|
|
линии: |
|
|
|
y |
16 x2 , |
|||||||||||||||||||||||||||||||||||
y 2 16 x2 , |
|
x2 |
y 2 |
16 . Значит, линия – окружность радиусом R = 4 с центром в точке |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
О(0, 0). Точнее, |
|
верхняя половина окружности, |
так как перед радикалом стоит знак «+» |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
( у 0) . Преобразуем уравнение второй линии: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y 4 16 x2 , ( y 4)2 16 x2 , x2 ( y 4)2 16 . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Данная линия – нижняя половина окружности радиуса R = 4 с центром в точке А(0, 4). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Линия х = 0 – прямая, совпадающая с осью Оу. Фигура изображена на рис. 2.21. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
164 xx22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 4 |
|
16 x2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–4 |
|
|
|
|
|
O |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Находим абсциссу точки В – точки пересечения окружностей. Решая систему уравнений
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
16 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
4 |
16 x |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
получаем: |
16 x2 4 |
16 x2 , |
16 x2 |
2, |
x2 |
12 . |
Так |
|
как |
х 0 , |
|
то |
х 2 3 , |
|||||||||||||||||||||||||
следовательно, искомая площадь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
3 |
|
|
|
16 x2 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
||||
|
S dxdy |
dx |
|
|
dy |
(2 |
16 x2 |
4)dx 2 |
|
|
16 x2 dx 8 |
3. |
|
|||||||||||||||||||||||||
|
D |
|
|
0 |
|
|
4 |
16 x2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||
Получившийся интеграл вычисляем с помощью подстановки x 4sin t : |
|
|
|
|||||||||||||||||||||||||||||||||||
2 3 |
16 x |
2 |
|
/ 3 |
|
|
2 |
|
|
|
/ 3 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
/ 3 |
|
8 |
2 |
3. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
dx 16 cos |
|
t dt 8 |
(1 cos 2t)dt 8 t |
2 |
sin 2t |
|
|
3 |
||||||||||||||||||||||||||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
8 |
2 |
|
|
|
|
3 |
16 |
|
4 |
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Таким образом, S 2 |
3 |
|
|
3 8 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
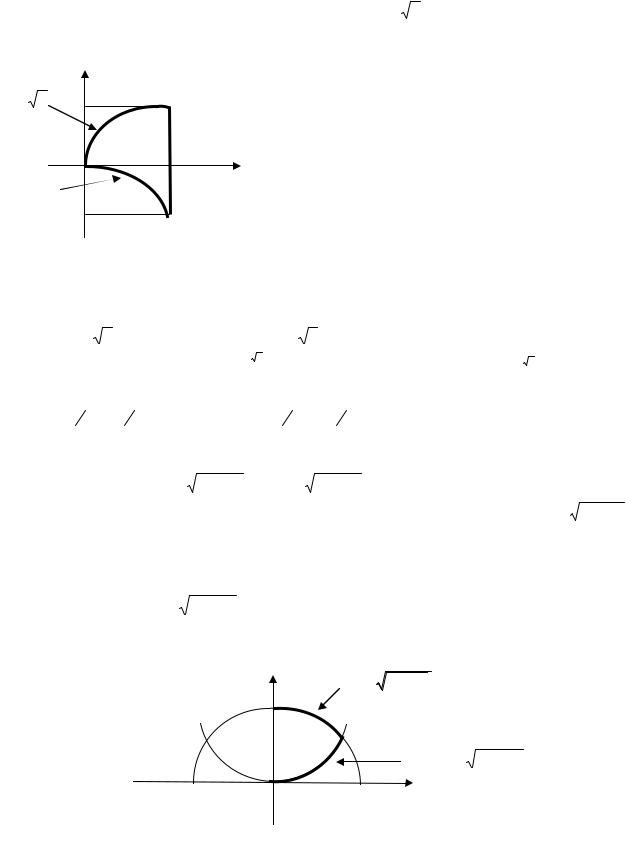
Задача 3. Пластинка D задана ограничивающими ее кривыми: х2 + у2 = 25, х2 + у2 = 36, |
||||||||||||||||||||||||||||||||||||||
х = 0, у = 0 |
(х 0, |
у 0) . |
Поверхностная |
плотность |
|
|
(х 4 у) (х2 |
у2 ) . |
Найти массу |
|||||||||||||||||||||||||||||
пластинки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Массу пластинки D (рис. 2.22) найдем по формуле (2.19). |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
M (x, y)dxdy . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Переходя в двойном интеграле к полярным координатам по формулам |
x r cos , |
|||||||||||||||||||||||||||||||||||||
x r sin , получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x 4 y |
|
|
2 |
6 |
|
r cos 4r sin |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
M |
|
|
|
|
|
|
|
|
dxdy |
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
rdr |
|
|
|
|
|||||||
|
|
|
|
|
2 |
y |
2 |
|
|
2 |
(cos |
2 |
sin |
2 |
) |
|
|
|
|
|||||||||||||||||||
|
|
|
|
D x |
|
|
|
|
|
0 |
|
5 r |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
2 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d (cos 4sin )dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
05
2
(cos 4sin )d (sin 4 cos ) 0  2 1 4 5.
2 1 4 5.
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
y |
х2 + у2 = 25 |
|
y |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
D |
|
|
5 |
A |
|
||
|
|
|
|
|
|
х2 + у2 = 36 |
|
|
||||
|
|
|
|
|
|
|
|
|
y x 5 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
O |
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||
5 |
|
6 |
O |
|
1 |
|||||||
|
|
|
|
|||||||||
|
|
Рис. 2.22 |
|
|
|
|
|
|
Рис. 2.23 |
|
||
63

Задача 4. Найти объем тела, заданного ограничивающими его поверхностями: y x 5, y
5, y  5x, z 0, x z 1.
5x, z 0, x z 1.
Решение. Для вычисления объема воспользуемся формулой
V dxdydz .
T
При переходе от тройного интеграла к повторному сначала проинтегрируем по z, затем по у и, наконец, по х. Снизу тело Т ограничено плоскостью z = 0, сверху – тоже плоскостью z = 1 – x. Проекцией тела Т на плоскость Оху является область D (рис. 2.23).
Найдем абсциссу |
точки А – точки пересечения линий y x 5 |
и |
y 5x . Решая |
|
систему уравнений y x |
5 , находим х = 0 и х = 1, откуда хА = 1. Значит, переменная х |
|||
|
|
5x |
|
|
y |
|
|
||
изменяется от 0 до 1, |
переменная у – от значения на прямой y x |
5 |
до значения на |
|
параболе y  5x .
5x .
Таким образом, имеем
|
|
|
|
|
|
|
|
1 |
|
5x |
1 x |
|
1 |
5x |
|
|
|
|
|
|
|
|
|||
|
V dxdydz dx |
dy dz |
dx (1 x)dy |
|
|
|
|||||||||||||||||||
|
|
T |
|
|
|
|
|
0 |
x |
5 |
0 |
|
|
0 |
x |
5 |
|
|
|
|
|
|
|
|
|
|
1 (1 x)( 5x x 5)dx 5 1 ( |
|
x x x x x2 )dx |
|
|||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 3 2 |
|
2 5 2 |
|
|
x2 |
|
x3 |
|
2 2 1 |
|
1 |
5 |
|
|||||||||
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
5 |
3 |
5 |
|
2 |
3 |
|
3 |
5 |
2 |
10 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||||
Задача 5. Тело Т задано ограничивающими его поверхностями: x2 + y2 = z2, x2 + y2 = z, |
|||||||||||||||||||||||||
x = 0, y = 0 (х 0, |
у 0) . Плотность |
24z . Найти массу тела. |
|
|
|
|
|||||||||||||||||||
Решение. Сделаем чертеж (рис. 2.24). Найдем уравнение линии пересечения поверхностей: x2 + y2 = z2, x2 + y2 = z. Исключая из этих уравнений x2 + y2, получаем z2 = z,
откуда z = 1, т. е. x2 + y2 = 1 (случай z = 0 дает единственную точку х = у = z = 0). |
|
|||||||||||
Значит, линией пересечения поверхностей является |
окружность |
x2 + y2 = 1, |
z = 1, |
|||||||||
поэтому |
в проекции тела |
Т на |
плоскость |
Оху получается |
область |
D – четверть |
круга |
|||||
(рис. 2.24) с границей x2 + y2 = 1. |
|
|
|
|
|
|
|
|
|
|
||
|
z |
|
Массу тела Т находим по формуле |
|
||||||||
|
|
|
|
|||||||||
|
|
|
|
|
M (x, y, z)dxdydz . |
|
||||||
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
Вычисление тройного интеграла упрощается, если |
|||||||||
|
|
|
перейти |
к |
цилиндрическим |
координатам: |
||||||
|
|
|
x r cos , y r sin , z z . Поверхность x2 + y2 = z в |
|||||||||
|
|
у |
цилиндрических координатах имеет уравнение z = r2, |
|||||||||
|
О |
поверхность |
z |
x2 |
y2 |
– |
|
|
уравнение |
z = r, |
||
|
D |
|
следовательно, z изменяется от r |
2 |
до r. Переменная r |
|||||||
|
|
|
|
|||||||||
х |
x2 + y2 = 1 |
|
изменяется от 0 до 1, |
переменная φ – от 0 |
до π/2 |
|||||||
|
(рис. 2.24). Поэтому |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
Рис. 2.24 |
|
2 |
1 |
r |
|
2 |
1 |
|
|
2 |
|
|
|
M d rdr 24zdz 12 d r(r2 r4 )dr d 2 . |
||||||||||
|
|
|
0 |
0 |
r2 |
|
0 |
0 |
|
|
0 |
|
64

Расчетное задание
Задача 1. Вычислить:
1. |
(12x2 y 2 |
16x3 y3 )dxdy; |
D : x 1, y x2 , y x . |
||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
2. |
(9x2 y 2 |
48x3 y3 )dxdy; |
D : x 1, y |
x, y x2 . |
|||||||
|
D |
|
|
|
|
|
|
|
|
|
|
3. |
(8xy 9x2 y 2 )dxdy; D : x 1, y 3 |
x, y x3 . |
|||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
4. |
(4xy 16x3 y3 )dxdy; |
D : x 1, y x3 , y 3 |
x . |
||||||||
|
D |
4 xy |
|
|
9 |
|
|
|
|
|
|
5. |
( |
|
|
x2 y2 )dxdy; |
D : x 1, y x3 , y |
x . |
|||||
|
|
|
|||||||||
|
D |
5 |
11 |
|
|
|
|
|
|||
6. |
( |
4 xy 9x2 y2 )dxdy; |
D : x 1, y |
x, y x3 . |
|||||||
|
D |
5 |
|
|
|
|
|
|
|
|
|
7. |
(36x2 y 2 |
96x3 y3 )dxdy; |
D : x 1, y 3 x, y x3 . |
||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
8. |
(18x2 y 2 |
32x3 y3 )dxdy; |
D : x 1, y 3 |
x, y x2 . |
|||||||
|
D |
|
|
|
|
|
|
|
|
|
|
9. |
(xy 4x3 y3 )dxdy; D : x 1, y x3 , y x . |
||||||||||
|
D |
|
50 x4 y4 )dxdy; |
|
|
|
|
||||
10. |
(3x2 y2 |
D : x 1, y 3 |
x, y x3 . |
||||||||
|
D |
|
|
|
3 |
|
|
|
|
|
|
Задача 2. Найти площадь фигуры, ограниченной данными линиями:
1. |
x 36 y2 , x 6 36 y2 . |
||||
2. |
x2 |
y2 |
72, |
6 y x2 |
( y 0) . |
3. |
x2 |
y2 |
36, |
3 2 y x2 |
( y 0) . |
4.y  24 x2 , 2
24 x2 , 2 3y x2 , x 0 (x 0) .
3y x2 , x 0 (x 0) .
5.y  12 x2 , y 2
12 x2 , y 2 3
3  12 x2 , x 0 (x 0) .
12 x2 , x 0 (x 0) .
6. x2 y2 |
12, |
6 y x2 |
( y 0) . |
7.y  36 x2 , y 6
36 x2 , y 6  36 x2 .
36 x2 .
8.y  6 x2 , y
6 x2 , y  6
6  6 x2 .
6 x2 .
9. |
x 72 y2 , 6x y2 , y 0 ( y 0) . |
10. |
x2 y2 12, x 6 y2 (x 0) . |
Задача 3. Пластинка D задана ограничивающими ее кривыми, – поверхностная плотность. Найти массу пластинки.
1. |
D : x2 |
y2 |
1, |
x2 |
y2 |
4, x 0, y 0 (x 0, y 0); |
(x y) (x2 |
y2 ) . |
|||||
2. |
D : x2 |
y2 |
4, |
x2 |
y2 |
25, |
x 0, |
y 0 |
(x 0, y 0); |
|
(2x 3y) |
|
(x2 y2 ) . |
3. |
D : x2 |
y2 |
9, |
x2 |
y2 |
25, |
x 0, |
y 0 |
(x 0, y 0); |
|
(2 y x) |
(x2 y2 ) . |
|
65
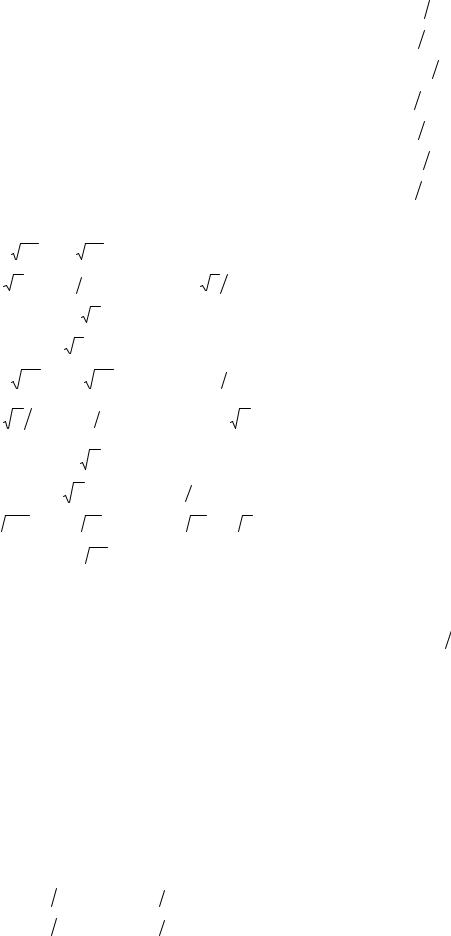
4. |
D : x2 |
y2 |
4, |
x2 |
y2 |
16, |
x 0, |
y 0 |
(x 0, y 0); |
(3x y) (x2 y2 ) . |
||
5. |
D : x2 |
y2 |
4, |
x2 |
y2 |
9, |
x 0, |
y 0 |
(x 0, y 0); |
( y 4x) |
(x2 |
y2 ) . |
6. |
D : x2 |
y2 |
9, |
x2 |
y2 |
16, |
x 0, |
y 0 |
(x 0, y 0); |
(2x 5y) (x2 y2 ) . |
||
7. |
D : x2 |
y2 |
1, |
x2 |
y2 |
16, |
x 0, |
y 0 |
(x 0, y 0); |
(x y) |
(x2 |
y2 ) . |
8. |
D : x2 |
y2 |
4, |
x2 |
y2 |
9, |
x 0, |
y 0 |
(x 0, y 0); |
( y 2x) |
(x2 |
y2 ) . |
9. |
D : x2 |
y2 |
1, |
x2 |
y2 |
25, |
x 0, |
y 0 |
(x 0, y 0); |
(x 4 y) (x2 y2 ) . |
||
10. |
D : x2 |
y2 |
1, |
x2 |
y2 |
9, x 0, y 0 (x 0, y 0); (2x y) |
(x2 |
y2 ) . |
||||
Задача 4. Найти объем тела, заданного ограничивающими его поверхностями. |
||||||||||||
1. |
y 16 |
2x, y |
2x, z 0, x z 2 . |
|
|
|
|
|||||
2. |
y 5 |
x, y 5x 3, z 0, z 5 5 x 3 . |
|
|
|
|
||||||
3. |
x2 y2 2, y |
x, y 0, z 0, z 15x . |
|
|
|
|||||||
4. |
x y 2, y |
x, z 0, z 12y . |
|
|
|
|
|
|||||
5. |
x 20 2 y , x 5 2 y, z 0, z y 1 2 . |
|
|
|
|
|||||||
6. |
x 5 |
y 2, x 5y 6, z 0, z 5 (3 y ) . |
|
|
|
|||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
7. |
x2 y 2 2, x |
y , x 0, z 0, z 30 y . |
|
|
|
|||||||
8. |
x y 2, x |
y, z 0, z 12x 5 . |
|
|
|
|
|
|||||
9.y  15x, y x
15x, y x 15, z 0, z
15, z 0, z  15(1
15(1  x) .
x) .
10.x2 y2 8, y  2x, y 0, z 0, z 15x
2x, y 0, z 0, z 15x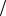 11 .
11 .
Задача 5. Тело Т задано ограничивающими его поверхностями, |
– плотность. Найти |
|||||||||||||||||
массу тела. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
64(x2 y2 ) z 2 , |
x2 |
y2 |
4, |
y 0, z 0 ( y 0, z 0); 5(x2 |
y2 ) 4 . |
||||||||||||
2. |
x2 |
y2 |
1, |
x2 |
y2 |
|
2z, |
|
x 0, |
y 0, z 0 |
(x 0, y 0); |
10x . |
||||||
3. |
x2 |
y2 |
z 2 |
|
1, |
x2 |
y2 4z 2 , |
x 0, |
y 0, |
(x 0, y 0, z 0); 20z . |
||||||||
4. |
36(x2 y2 ) |
z 2 , |
x2 |
y2 |
1, x |
0, z 0 (x 0, z 0); 5(x2 y2 ) / 6 . |
||||||||||||
5. |
x2 |
y2 |
4, |
|
x2 |
y2 |
|
8z, |
x 0, |
y 0, z 0 |
(x 0, y 0); |
5x . |
||||||
6. |
x2 |
y2 |
|
4 |
|
z 2 |
, |
x2 |
y2 |
2 z, |
x 0, |
y 0, |
(x 0, y 0); |
28xz . |
||||
|
|
|||||||||||||||||
|
|
|
25 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
||
7. |
x2 |
y2 |
z 2 |
|
4, |
x2 |
|
y2 |
z 2 , |
x 0, |
y 0, |
(x 0, y 0, z 0); |
6z . |
|||||
8. |
25(x2 y2 ) |
z 2 , |
x2 |
y2 |
4, |
x 0, y 0 z |
0 (x 0, y 0, z 0); 2(x2 y2 ) . |
|||||||||||
9. |
x2 |
y2 |
z 2 |
|
25, |
x2 |
|
y2 |
z 5, |
x 0, |
y 0, |
(x 0, y 0); |
14 yz . |
|||||
10. |
x2 |
y2 |
z 2 |
|
49, |
x2 |
|
y2 |
z 7 , |
x 0, |
y 0, |
(x 0, y 0); |
10xz . |
|||||
66
ГЛАВА 3. КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
3.1. Криволинейные интегралы
Криволинейные интегралы являются обобщением определенного интеграла на случай, когда областью интегрирования является некоторая плоская или пространственная кривая. Различают два типа криволинейных интегралов: криволинейные интегралы первого и второго рода.
3.1.1. Задача, приводящая к понятию криволинейного интеграла первого рода
К понятию криволинейного интеграла первого рода приводят различные физические задачи, например, задача о вычислении массы материальной линии.
Пусть на некоторой плоской кривой AB непрерывно распределена масса. Предположим, что кривая AB гладкая или кусочно-гладкая. Здесь и в дальнейшем кривую будем называть гладкой, если в каждой ее точке существует касательная, и при переходе от точки к точке положение этой касательной меняется непрерывно. Кусочно-гладкой кривой называется непрерывная кривая, составленная из конечного числа гладких кривых.
Найдем массу m материальной кривой AB, если известна плотность γ кривой в каждой ее точке M(x, y), т. е. γ = γ(x, y), где γ(x, y) – непрерывная функция вдоль кривой AB.
Непрерывность функции γ(x, y) = γ(M) вдоль кривой AB означает, что lim M M0 в
M M0
любой точке M0 кривой AB, где М также точка этой кривой.
Разобьем кривую AB произвольно на n частей точками А = А0, А1, А2, …, Аn–1, Аn = В (рис. 3.1).
y |
|
|
Mn |
|
An–1 B = An |
|
M2 |
M1 |
A2 |
|
A1 |
|
A = A0 |
О |
x |
Рис. 3.1
На каждой из дуг Аi–1Аi (i = 1, 2, …, n) произвольно выберем точку Мi(xi, yi) и найдем в этих точках плотность γ(xi, yi). Массу mi дуги Аi–1Аi можно считать приближенно равной
γ(xi, yi) si, где si – длина дуги Аi–1Аi. Суммируя массы всех дуг разбиения, получим приближенное значение массы m кривой AB:
n |
|
m xi , yi si . |
(3.1) |
i 1
67
Так как функция γ(x, y) непрерывна, то чем «мельче» разбиение кривой AB, тем точнее равенство (3.1). Массой материальной кривой называется предел правой части равенства
(3.1) при λ →0, т. е.
n
m lim xi , yi si , (3.2)
0 i 1
где λ – наибольшая из длин частичных дуг Аi–1Аi (λ max si . Таким образом, вычисление
1 i n
массы кривой сводится к вычислению предела (3.2).
3.1.2. Определение криволинейного интеграла первого рода, его физический и геометрический смысл
Рассмотрим на плоскости Оху гладкую или кусочно-гладкую кривую АВ, в каждой точке которой задана произвольная непрерывная функция z = f(x, y). Повторяя последовательно все операции, выполненные при составлении правой части равенства (3.1), составим сумму
n |
|
f xi , yi si , |
(3.3) |
i 1
которая называется интегральной суммой для функции f(x, y) по кривой АВ.
Определение 3.1.1. Если при λ →0 интегральная сумма (3.3) имеет предел, который не зависит ни от способа разбиения кривой АВ на части, ни от выбора точек Мi, то этот предел называется криволинейным интегралом первого рода от функции f(x, y) по кривой АВ и
обозначается символом
|
f x, y ds . |
|
|
|
|
||
Таким образом, |
AB |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
f x, y ds lim |
f x |
, y |
s |
i |
. |
|
0 |
|
i |
i |
|
|
||
AB |
|
i 1 |
|
|
|
|
|
Криволинейный интеграл первого рода называют также криволинейным интегралом по длине дуги.
Заметим, что криволинейный интеграл первого рода не зависит от направления кривой АВ. Действительно, в интегральной сумме (3.3) величины si положительны, независимо от того, какую точку кривой АВ считать начальной, а какую – конечной, т. е.
f x, y ds f x, y ds .
AB |
ВA |
Из соотношения (3.2) следует физический смысл криволинейного интеграла первого рода: масса m материальной кривой АВ, имеющей плотность γ(x, y), равна криволинейному интегралу первого рода от γ(x, y) по кривой АВ, т. е.
m x, y ds .
AB
Помимо массы материальной кривой с помощью криволинейных интегралов первого рода можно также, как это делали в случае двойных интегралов, находить статистические моменты и моменты инерции этой кривой относительно координатных осей, координаты центра масс и т. д.
68
Криволинейный интеграл первого рода, так же как и определенный интеграл, имеет
геометрический смысл. Если определенный интеграл b f x ds при f(x)≥0 представляет собой
a
площадь криволинейной трапеции, то криволинейный интеграл f x, y ds при f(x,y)≥0
AB
численно равен площади цилиндрической поверхности, которая составлена из перпендикуляров к плоскости Оху, восстановленных в точках М(х, у) кривой АВ и имеющих переменную длину f(x, y) (рис. 3.2).
z
z = f(x,y)
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
x |
|
|
|
|
|
|
|
M(x,y) |
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Рис. 3.2 |
|
||
В частности, если |
f x, y 1 , то |
ds l , где l – длина кривой АВ. |
||||||||||
|
|
|
|
|
|
|
AB |
|
||||
3.1.3. Вычисление криволинейного интеграла первого рода
Вычисление криволинейных интегралов первого рода сводится к вычислению определенных интегралов.
Пусть кривая АВ задана параметрическими уравнениями x = x(t), y = y(t) (α ≤ t ≤ β).
Для определенности будем считать, что точке А соответствует значение t = α, точке В – значение t = β. Тогда криволинейный интеграл выражается через определенный интеграл по формуле
|
|
|
|
|
f x, y ds f x t , y t |
xt 2 |
yt 2 dt . |
(3.4) |
|
AB |
|
|
|
|
В частности, если кривая АВ задана уравнением y = y(х), а ≤ х ≤ b, то, принимая х за параметр (t = x), из формулы (3.4) получаем
|
f x, y ds b |
f x, y x |
1 yx 2 dx . |
(3.5) |
AB |
a |
|
|
|
69

Пример |
|
3.1.1. Вычислить |
криволинейный |
интеграл |
x y ds , |
где |
АВ – |
часть |
||||||||||||||||
окружности: x = acost, y = asint (0 ≤ t ≤ π). |
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Так как |
xt asin t , yt a cost , |
xt 2 |
yt 2 |
|
a2 sin 2 t a2 |
cos2 t a , то |
||||||||||||||||||
по формуле (3.4) получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x y ds a cost sin t adt a2 sin t cost |
|
0 |
2a2 . |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
AB |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3.1.2. Вычислить криволинейный интеграл x2 ds |
по кривой АВ, заданной |
|||||||||||||||||||||||
уравнением: у = lnx, 1 ≤ х ≤ 2. |
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. |
Имеем |
yx 1 , |
1 yx 2 |
|
|
1 |
1 |
|
|
1 x2 |
|
. Применяя |
формулу |
(3.5), |
||||||||||
|
|
|
x |
|||||||||||||||||||||
получим |
|
|
|
|
x |
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
x2 ds 2 x2 |
1 x2 |
|
dx 2 x |
1 x2 dx |
1 |
2 |
1 x2 d 1 x2 |
1 х2 32 |
|
|
5 5 2 2 . |
|
||||||||||||
|
|
|
||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|||||||||||||||
AB |
1 |
|
1 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
3 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.1.4. Криволинейный интеграл второго рода и его физический смысл
Рассмотрим физическую задачу, которая естественным путем приводит к понятию криволинейного интеграла второго ряда и позволяет выяснить его физический смысл.
Предположим, что материальная точка перемещается по плоской кривой АВ из положения А в положение В под действием силы F F x, y , которая задана своими проекциями P, Q на координатные оси, т. е.
y
Fi
yi |
∆yi |
|
Mi |
yi–1 |
|
Ai |
|
|
|
|
Ai-1 |
|
M2 |
A2 |
|
|
M1 |
|
|
|
A1 |
|
|
|
|
|
|
|
A = A0 |
∆xi |
|
|
|
|
|
О |
|
|
xi–1 xi |
Рис. 3.3
F P x, y i Q x, y j P,Q .
Mn
An–1
B = An
Найдем работу W силы F при перемещении точки из А в В вдоль заданной кривой.
Если бы перемещение точки было бы прямолинейным, а действующая сила
F – постоянной (по величине и направлению), то работа W этой силы, согласно известной из физики формуле, была бы равна скалярному произведению вектора
|
|
F |
на |
вектор |
перемещения |
АВ |
, т. е. |
||||||||
|
W |
|
|
|
. |
Однако |
особенность |
задачи |
|||||||
|
F, |
AB |
|||||||||||||
x |
состоит |
в |
том, |
что |
перемещение |
точки |
|||||||||
является |
криволинейным, |
а |
действующая |
||||||||||||
|
сила – переменной. |
|
|
|
|
|
|||||||||
|
|
|
|
В связи с этим разобьем кривую АВ на n |
|||||||||||
|
частей точками |
Аi (i = 0, |
1, |
…, |
n), |
А0 = А, |
|||||||||
|
Аn = В (рис. 3.3). |
|
|
|
|
|
|
||||||||
70
