Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ульяновский Государственный Педагогический Университет им. И. Н. Ульянова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ankilov

.pdf

Скачиваний:

Добавлен:

07.02.2015

Размер:

2.14 Mб

Скачать

☆

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 1516 / 2816 17 18 19 20 21 22 23 24 25 26 27 28 > Следующая >>>

					x	n
8.	Областью сходимости степенного ряда				x			является промежуток:
8.	Областью сходимости степенного ряда				n 10		n	является промежуток:
	а) (– 10, 10);			n 1	n 10
	а) (– 10, 10);
	б) (– 1, 1);
	в) [– 10, 10];
	г)	(– 1, 1];
	д) [– 10, 10).				x ,
9.	Если 2 -периодическую функцию			f (x)	x ,			x 0, 2 , разложить в ряд Фурье,
то сумма ряда в точке x 0 будет равна:					2
то сумма ряда в точке x 0 будет равна:
	а)		;
		2	;
	б)		;
	в) 0;		2
	в) 0;
	г)	;
	д) 2 .						f (x) задана и непрерывна на отрезке
10.	Выберите верные утверждения. Если функция						f (x) задана и непрерывна на отрезке
[0, l] и имеет на этом отрезке непрерывную производную								f / (x) , то на отрезке [0, l] функцию
f (x) :

а) можно разложить в ряд Фурье по синусам; б) можно разложить в ряд Фурье по косинусам; в) нельзя разложить в ряд Фурье;

г) можно разложить в ряд Фурье по синусам и косинусам.

5.7.2. Задачи
Образцы решения задач
	2	cos		n		3	n	2


Задача 1.1. Исследовать на сходимость ряд					2				.
Задача 1.1. Исследовать на сходимость ряд		2n	2		1				.
n 1		2n			1

Решение. К данному знакоположительному ряду применим признак сравнения

(теорема 5.1.2). Так как |cos x| ≤ 1, 2n2 + 1 > 2n2, то

cos

33 n2

2n2 1

2n2

n4 / 3

Обобщенный гармонический ряд (ряд Дирихле)

сходится при α > 1 и расходится

n 1

при α ≤ 1. Следовательно, ряд 3

сходится. Согласно признаку сравнения исходный

4 / 3

n 1

ряд также сходится.

151

Задача 1.2. Исследовать на сходимость ряд 3

n arcsin

n 1

Решение. Воспользуемся предельным признаком сравнения (теорема 5.1.3). Так как

arcsin

при n → ∞ , то

n 1

23 n

lim

n arcsin

lim

2 0 .

2 / 3

n 1

1 1/ n

n 1

Поскольку ряд

расходится, то исходный ряд также расходится.

2 / 3

n 1

! .

Задача 2.1. Исследовать на сходимость ряд 2

Решение.

n 1

Применим

признак

Даламбера

(теорема

5.1.4). Учитывая

то, что

n 1

2n 1 (n 1) !

, находим

(n 1)n 1

Un 1

2n 1 (n 1) ! 2n n !

2n 1 (n 1) !nn

2nn

lim

n 1 :

lim

n 1

lim

(n 1)

n (n 1)

Следовательно, по признаку Даламбера данный ряд сходится.

	n		2n
Задача 2.2. Исследовать на сходимость ряд		.
Задача 2.2. Исследовать на сходимость ряд	3n 1	.
n 1	3n 1

Решение. Так как lim n Un

n 2n

n 2

1 2

lim n

lim

1, то

3n 1

3 1/ n

согласно радикальному признаку Коши (теорема 5.1.5) данный ряд сходится.

Задача 3. Найти область сходимости степенного ряда

n 1

Решение. Радиус

n 1

сходимости

данного

степенного

ряда

находим по формуле

. Так как an

an 1

R lim

, то

an 1

3n 1

3n n 1

R lim

lim

3lim

3 ,

3n 1

n 1

3n 1 n

следовательно, ряд абсолютно сходится в интервале (–3, 3).

Исследуем поведение ряда на концах интервала сходимости. Подставляя в данный ряд

				3n			1
вместо х число 3, получим числовой расходящийся ряд						3		, так как ряд
вместо х число 3, получим числовой расходящийся ряд			3	n 1	n	3	n	, так как ряд
		n 1	3		n	n 1	n
	1
Дирихле	1	расходится при α ≤ 1. При х = – 3 получим числовой знакопеременный ряд
Дирихле
n 1	n

152

	3
( 1)n	3	, который сходится по признаку Лейбница (теорема 5.1.7). Сходимость условная,
( 1)n	n
n 1	n
				3		1

поскольку ряд из абсолютных величин			( 1)n		3		расходится.
поскольку ряд из абсолютных величин			( 1)n	n	3	n	расходится.
		n 1		n	n 1	n

Таким образом, областью сходимости данного степенного ряда является полузамкнутый интервал [–3, 3).

Задача 4. Вычислить интеграл 1

x2e x2 dx с точностью до 0,001.

Решение. Учитывая разложение et

, t , при t = –x2 будем иметь

n 0 n !

2 x2

( 1)n x2n

( 1)n 1

2n 2

( 1)n x2n 3

( 1)n

x e

dx x

n !

n !(2n

n 0

n 0 n !(2n 3)

n 0

( 1)n 1

1 1

n 1

3 5

... .

(n 1) !(2n 1)

264

1560

Мы получили знакочередующийся числовой ряд, удовлетворяющий условиям теоремы 5.1.7. Поэтому, если в качестве приближенного значения его суммы взять сумму первых n членов, то ошибка по абсолютной величине не будет превосходить абсолютной величины

первого отбрасываемого члена Un 1																							1				.
первого отбрасываемого члена Un 1																					n !(2n					3)	.
																					n !(2n					3)
	Так как U6					1			0,000641... 65 10 5																	0,001, то с точностью до 0,001 имеем
	Так как U6				1560				0,000641... 65 10 5																	0,001, то с точностью до 0,001 имеем
					1560
				1							5								( 1)			n 1					1	1			1		1		1
				x2e x2 dx															( 1)									1			1		1		1		0,190 .
				x2e x2 dx											(n 1) !(2n 1)																						0,190 .
				0						n 1					(n 1) !(2n 1)												3	5	14			54			264
	Задача 5. Разложить в ряд																			Фурье					2l-периодическую										функцию f (x) = 2x + 10,
– 2 < x < 2, l = 2. Построить график суммы ряда.
	Решение. Для вычисления коэффициентов Фурье воспользуемся формулами (5.32):
										an							1 l			f (x)cos					n x dx,			n 0,1, 2, ... ,
																	l l									l
										b 1 l										f (x)sin n x dx,								n 1, 2, 3, ....
											n						l l								l
																	l l								l
			1	2												2						2
Имеем: a0			1	(2x 10) dx									x											20 ,

			2											2						5x
			2	2										2								2
		2									2
an	1	(2x 10) cos n x dx									(x 5) cos n x dx .
	2	2					2				2												2
	Интегрируя по частям, получаем
						2				n x		2							2		2			n x						2		2		n x		2
						2				n x		2							2		2			n x						2		2		n x		2
		an	(x 5)					sin													sin						dx					cos					0, n 1, 2, 3, ....
		an	(x 5)					sin													sin						dx					cos					0, n 1, 2, 3, ....
						n				2		2						n			2				2			n						2		2

Аналогично находим

153

bn 2	(x 5) sin	n x	dx (x 5)					2			cos			n x			2	2	2 cos n x			dx 14 cos n	6	cos n
bn 2	(x 5) sin	2	dx (x 5)								cos			2				n	2 cos n x			dx 14 cos n	n	cos n
2		2						n						2			2	n	2	2		n	n
			2	2		n x				2				8		cos n				8( 1)n		n 1, 2, 3, ....
			2	2		n x				2				8						8( 1)n
				sin																	,
				sin																	,
		n					2			2				n						n
Подставляя найденные коэффициенты в формулу (5.33), получаем разложение функции
					8				( 1)			n			n x .
f (x) в ряд Фурье: f (x) 10					8				( 1)				sin
f (x) в ряд Фурье: f (x) 10													sin
							n 1			n						2

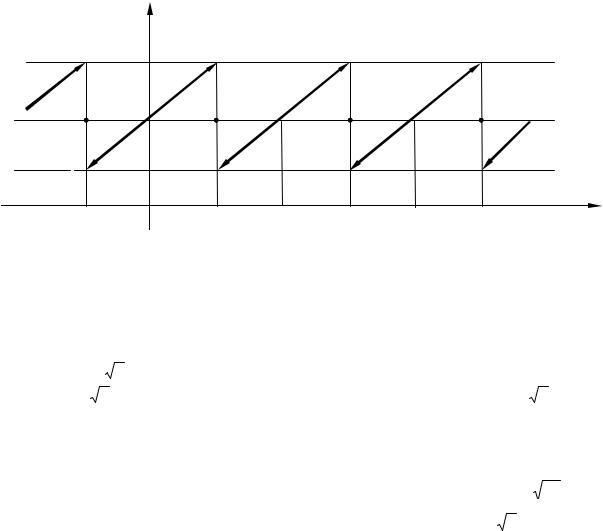
Построим график суммы ряда. Сумма ряда S (x) имеет период T = 2l = 4 и S (x) = f (x) в точках непрерывности f (x), т. е. для всех х ≠ 4k – 2, k = 0, + 1, + 2, ….

Если x 4k 2, то S(4k 2) S(2) 12 f (2 0) f (2 0) 12 (14 6) 10 (рис. 5.7).

S(x)

–2

Рис. 5.7

Расчетное задание

Задача 1. Исследовать на сходимость ряд.

1.			2	n		n .
1.	sin			n		n .
	n 1	n		n
		cos		2	(n / 2)
3.		cos			(n / 2)					.
3.										.
	n 1	n(n 1)(n 2)
5.		2 ( 1)					n
5.		2 ( 1)					.
	n 1	n ln n
7.		n(2 cos n )							.
7.			2n		2	1			.
	n 1		2n			1
		3 ( 1)n
9.								.
9.			2	n				.
	n 1		2

Задача 2. Исследовать на сходимость ряд.

	n	2
1.	n			.
1.	(n		2)!	.
n 1	(n		2)!

2.	1	tg				1 .

	n 1 n
	n 1 n					n
			n		2	5
4.	ln		n			5	.
4.	ln		n		2		.
	n 1		n			4
						1
6.	nsin					1			.
6.	nsin								.
	n 1					3 n4
								1
8.	3	n arctg						1			.
8.	3	n arctg									.
	n 1							n3
				cos
10. 1				cos				n		.
	n 1							n
		2n			2	1	n2
2.		2n				1
				2
		n		2		1	.
	n 1	n				1

154

		arctg		5
3.				n		.
3.		n!				.
	n 1	n!
5.		(n 1)!					.
5.		n	n				.
	n 1	n

7.	n!sin							.
7.	n!sin				n			.
9.	n 1			2
9.	n! .

n 1 (3n)!

Задача 3. Найти область сходимости степенного ряда.

		3	(n				1)				n
1.			(n				1)						xn .
1.				n!									xn .
	n 1			n!
		(2n)!x						n
3.		(2n)!x								.
3.		n								.
	n 1		n
			nx			n
5.			nx									.
5.		3	n									.
	n 1	3	(n 1)
7.				1			n				x		n	.
7.	1			n							x			.
	n 1			n
			3		n		x		n
9.			3				x								.
9.															.
	n 1		2n (3n 1)

Задача 4. Вычислить интеграл с точностью до 0,001.

1.	1 cos x2 dx .
	0
	0,1	e 2 x dx .
3.	1	e 2 x dx .
	0		x
	0,2
5.	e 3x2 dx .
	0
7.	0,5sin x2
7.		x	2	dx .
	0	x
	0,5
9.	ln(1 x2 ) dx ;
	0			x

	1			n		n2
4.					.
	3	n
n 1			n 1

2n 1

6.n 1 nn .


8.	2n 1e n .
	n 1
						2n 1								n
						2n 1							2			.
10.						3n 1										.
	n 1					3n 1
				2		n		x	n
2.				2				x				.
2.			n(n 1)									.
	n 1		n(n 1)
				3			n	n!
4.				3				n!			xn .
4.								n			xn .
	n 1		(n 1)
6.			5	n		x		n	.
6.			5			x			.
	n 1		n			n
			(n			1)x						n
8.			(n			1)x								.
8.				n										.
	n 1		3		(n 2)
				(n 2)x										n
10.				(n 2)x											.
10.															.
	n 1				n(n 1)
	0,1
2.	sin(100x2 )dx .
	0
4)	1 ln(1 x / 5) dx .
	0						x
	0,5			dx
6.				dx						.
6.		3	1 x						3	.
	0		1 x
	0,5
8.	x ln(1 x2 )dx .
	0
	0,5

10. e x2 / 3dx .

Задача 5. Разложить в ряд Фурье 2l-периодическую функцию y f (x) . Построить график суммы ряда.

1.	f (x) 2x 1, – 1 < x < 1, l = 1.	2.	f (x) 3x 2 , – 2 < x < 2, l = 2.
3.	f (x) 1 3x , – 3 < x < 3, l = 3.	4. f (x) 1 4x , – 4 < x < 4, l = 4.
5.	f (x) 5 x , – 2 < x < 2, l = 2.	6. f (x) 6 x , – 1 < x < 1, l = 1.
7.	f (x) 2x 1, – 4 < x < 4, l = 4.	8.	f (x) 1 4x , – 3 < x < 3, l = 3.
9.	f (x) 3x 1, – 1 < x < 1, l = 1.	10. f (x) 2x 1, – 2 < x < 2, l = 2.

155

ГЛАВА 6. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

6.1. Дифференциальные уравнения первого порядка

6.1.1. Основные понятия

	Дифференциальным уравнением (д. у.) называется уравнение, связывающее
независимую				переменную	x ,		функцию y y(x)	переменной x и ее	производные
		(n)	:			(n)	) 0 . Наивысший	порядок производной,	входящей в
y , y ,...y				F(x, y, y , y ,..., y

уравнение, называется порядком д. у. Решением д. у. на интервале (a;b) называется функция y (x) такая, что подстановка ее в д. у. превращает это уравнение в тождество по x на

(a;b) . График решения д. у. называется интегральной кривой этого уравнения.
Пример 6.1.1. Уравнение xy' x y	имеет порядок n = 1. Функция y x ln x является
решением уравнения. Действительно,	y' ln x 1; подставляя в уравнение, получим

x(ln x 1) x x ln x – тождество. Легко убедиться в том, что функция	y x ln x x также
является решением.


Пример 6.1.2. Уравнение y'' y 0 является д. у. второго			порядка. Функция y cos x
является решением. Действительно, y' sin x ,		y'' cos x ;	подставляя в уравнение,
получаем тождество: cos x cos x 0 . Функция	y sin x также является решением, а также
функции y sin x cos x , y 2sin x , y 3cos x ,	y 5cos x .

Рассмотренные примеры показывают, что д. у. может иметь несколько решений. Рассмотрим д. у. 1-го порядка, разрешенное относительно производной: y f (x, y) ,

где f (x, y) – некоторая функция двух переменных. Пусть даны числа x0 , y0 .

Задача Коши для д. у. 1-го порядка формулируется следующим образом: найти решение д. у. y f (x, y) , удовлетворяющее начальному условию y(x0 ) y0 . Геометрически

это означает,	что требуется найти интегральную		кривую, проходящую через точку
M 0 (x0 , y0 ) на плоскости xOy .
Пример 6.1.3. Дана задача Коши:		y' y x2 , y(0) 1. В этом случае		f (x, y) y x2 ,
x0 0 , y0 1,	M 0 (0;1) .	y f (x, y) ,
Теорема	6.1.1. Пусть дано д. у.		где функция f (x, y)	определена в

некоторой области D плоскости xOy , содержащей точку M 0 (x0 , y0 ) . Пусть выполняются условия:

1.f (x, y) есть непрерывная функция двух переменных в области D ;

2.f (x, y) имеет частную производную f y (x, y) , ограниченную в D .

Тогда найдется интервал (x0 h; x0 h) , на котором существует единственное решение

данного уравнения, удовлетворяющее условию y(x0 ) y0 .
Пример 6.1.4. Рассмотрим задачу Коши: y y 23 ,				y(0) 1. Здесь		f (x, y) y 23 –
непрерывная функция на всей плоскости xOy ; f y (x, y)		2	y	1	3 . По условию,	x0 0,	y0 1.
		3

В окрестности точки M 0 (0;1) частная производная f y (x, y)				ограничена, значит, все условия
теоремы	6.1.1 выполняются. Задача Коши имеет единственное решение.					Заметим, что
f y (x, y)	обращается в бесконечность при y 0 , т. е. на оси Ox , поэтому в точках оси Ox

возможно нарушение единственности. 156

Пусть дана задача Коши, и в области D выполняются условия теоремы 6.1.1. Общим

решением д. у. y		f (x, y) называется функция	y (x,C) , зависящая от переменной x и
константы C , удовлетворяющая условиям:
1.	При любом значении C функция y (x,C) является решением уравнения.
2.	При любом	начальном условии y(x0 ) y0 , таком,		что M 0 (x0 ; y0 ) D , найдется
значение константы		C , при котором функция	y (x,C)	будет удовлетворять данному

условию.

Частным решением д. у. называется решение, полученное из общего при каком-либо фиксированном значении константы C . Общим интегралом д. у. называется уравнение вида(x, y,C) 0 , неявно определяющее общее решение д. у. Решение y (x) д. у. называется

особым, если в каждой точке его графика нарушается свойство единственности, т. е. если через каждую точку M 0 (x0 ; y0 ) , кроме интегральной кривой этого решения, проходит также

интегральная кривая другого решения д. у.

Пример 6.1.5. Доказать, что функция	y (x C)3 / 27 является общим решением д. у.
y y 23 в области D : y 0 .
Решение. Находим производную: y	1	3(x C)	2	(x C)	2	/ 9 и подставляем	y и y
Решение. Находим производную: y	27	3(x C)		(x C)		/ 9 и подставляем	y и y

в уравнение: (x C)2		/ 9 (x C)3 / 27		23 – получили верное равенство. Пусть дано условие
y(x0 ) y0 , где	y0 0 . Тогда		y0 (x0 C)3 / 27		, C 3y013	x0 . Это означает, что при данном
значении С функция y (x C)3 / 27				удовлетворяет условию y(x0 ) y0 . Значит, y есть
общее решение.			y 0	также	является	решением д. у., это проверяется
Заметим,	что	функция

непосредственно. Пусть начальное условие имеет вид y(x0 ) 0 . Тогда этому условию будут удовлетворять два решения: y 0 и y (x C0 )3 / 27 , где C0 x0 . Поэтому решение y 0 есть особое решение дифференциального уравнения.

6.1.2. Уравнения с разделяющимися переменными

Признак. Дифференциальное уравнение первого порядка с разделяющимися

переменными

имеет

вид dy / dx P(x)Q( y)

или

P1 (x)Q1 ( y)dx P2 (x)Q2 ( y)dy 0 ,

где

P, Q, P1 , Q1 , P2 , Q2

– некоторые функции.

Метод решения. Следует разделить переменные, то есть привести уравнение к виду

P(x)dx

или

Q2 ( y) dy

P1 (x)

проинтегрировать

обе

части

уравнения

по

Q( y)

Q ( y)

P (x)

соответствующей переменной.

Пример 6.1.6. Найти общий интеграл уравнения: x2 8 y3

1 x3 y .

Решение.

Производную

y представим по формуле

как отношение двух

дифференциалов.

Уравнение

принимает

вид x2

8 y3

1 x3 dy .

Разделяем

y ,

уравнении переменные (т. е.

все множители,

содержащие

переносим в правую часть

157

уравнения,

а все множители с x –

в левую),

получаем:

x2 dx

2 dy

. Интегрируем:

1 x3

8 y3

x2 dx

y2 dy

. Вычисляем каждый

из

полученных

интегралов методом

замены

1 x

8 y

переменной:

x2 dx

1/ 2

t 1

1 t

2 dt 1

1 x3 C,

3 1/ 2

1 x

y 2 dy

8 y3 C.

8 y

Общий интеграл дифференциального уравнения есть:

2 1 x3 C 2

8 y3 , где

C – произвольная постоянная. Сокращая обе части уравнения на (–2/3) и заменяя число C

на другую константу C 3 C , получаем:

1 x3 C

8 y3 .

Замечание: решением уравнения является также y 2 , которое не входит в общий

интеграл и которое мы потеряли, производя деление на

8 y3 .

Это решение является

особым.

6.1.3. Однородные уравнения первого порядка

Признак. Однородное дифференциальное уравнение 1-го порядка имеет вид

f x

или P(x, y)dx Q(x, y)dy 0 , где P(x, y)

и Q(x, y)

– однородные функции от x

одного

порядка.

Последнее

означает,

что

для

любых

x , y ,

P( x, y) n P(x, y),Q( x, y) nQ(x, y) , где n – некоторое число.

–

новая

функция

Метод

решения. Подстановка

y xu(x), y

u x u ,

где u(x)

переменной

x . Подстановка приводит однородное уравнение

уравнению с

разделяющимися переменными xu f (u) u или xu u P(1, u) / Q(1, u) .

	Замечание.				Уравнение		вида	dy
								dx
dy1				by1				dy1
		ax1
dx		f			,	то	есть	dx
			a x	b y
1		1 1		1 1				1
x x1		h,		y y1	k ,	если	ab1 a1b 0 .

	ax by			c
	ax by			c		приводится к		однородному
				c
f a x b y				c
	1		1	1

	a by1 / x1
	f					с	помощью		замены
	f	a	b y / x			с	помощью		замены
	1		1	1	1
Постоянные					h,	k определяются		из	системы

уравнений ah bk c 0,	a h b k c				0 . Если же ab a b 0			(то есть	a1	b1	), то
уравнений ah bk c 0,	a h b k c				0 . Если же ab a b 0			(то есть		b1	), то
	1	1	1			1	1		a	b
его можно привести к виду									a	b
его можно привести к виду
		dy			ax by c
		dy			ax by c
		dx		f		.
		dx		f	(ax by) c	.
					1

158

Последнее уравнение с помощью введения новой функции z(x) ax by(x) приводится к уравнению с разделяющимися переменными

		z c
z		z c
		z c
	a bf	z c	.
		1

Пример 6.1.7. Найти общий интеграл уравнения xy

x cos

x .

Решение.

Разделим обе части уравнения на

x :

y / x cos2 ( y / x) . Правая часть

уравнения

зависит от

y / x ,

поэтому уравнение является

однородным.

Сделаем

замену

y xu(x),

u(x) .

или

u .

Разделим

xu (x)

Получим u x u u cos

u x cos

переменные:

du / cos2 u dx / x ; интегрированием

находим

tgu ln

C ,

где

C –

произвольная

постоянная

интегрирования. Общий

интеграл

исходного

уравнения:

tg( y / x) ln x C . В процессе решения мы делили на cos2 u , что могло привести к потере

решения. Положим cosu 0 ,

n Z . Эти

функции также являются

тогда y x

n ,

решениями исходного уравнения.

Пример 6.1.8. Найти общий интеграл уравнения y

y 2x 1

x y 2

Решение. Это уравнение, приводящееся к однородному.

Сделаем замену x x1 h,

y y1

k . Тогда уравнение примет вид

dy1

( y1 2x1 ) (k 2h 1)

(x y ) (h k 2)

Выбирая k 2h 1 0,

h k 2

0 ,

т. е.

h 1,

k 3 ,

и поделив

числитель и

знаменатель дроби на

x1 , получим однородное уравнение dy1 / dx1 y1 / x1

2 / 1 y1 / x1 ,

которое заменой y1 x1u(x1 )

приводится к уравнению с разделяющимися переменными:

x1du / dx1 u u 2 / 1 u .

1 u

du dx1 ,

Разделяя переменные и интегрируя, имеем

u2 2

u 2

1 In

u 2 2

2 2

u 2

2In

u 2

2In

u 2

2 2In

(1 2)In u 2 (1 2In u 2 2 2In x1 In C1 ,

(u 2)1 2 /(u 2)1 2 C1 x2 2 .

159

y 3

Возвращаясь к переменным

x 1

y u x

, общий интеграл уравнения запишем

в виде

y 3

1 2

y 3

1 2

C1x

2 2

x 1

6.1.4. Линейные уравнения первого порядка. Уравнения Бернулли

Признак. Линейное уравнение 1-го порядка имеет вид


		y P(x) y Q(x) ,				(6.1)
где P(x), Q(x)	– заданные функции, непрерывные на интервале (a,b) .
Метод решения. Следует искать решение уравнения в виде произведения двух
функций: y(x) U (x)V (x) . Подставляя			в (6.1), получим VU PV V U Q . Функцию V
определяют из	условия PV V 0		(тогда V C exp P(x)dx ,			где постоянную
интегрирования	C можно без ограничения			общности выбрать	равной	единице), затем
находят U из уравнения VU Q (тогда U Q /V dx C, C –					произвольная постоянная
интегрирования). Общее решение уравнения (6.1) имеет вид
	y exp	P(x)dx C
	y exp	P(x)dx C		Q(x) exp P(x)dx dx . .

Замечание. Решение можно получить также методом вариации произвольной постоянной, который для линейного уравнения первого порядка эквивалентен указанному

выше	методу: сначала находят	общее	решение	однородного уравнения
V P(x)V 0, V C exp P(x)dx , а		затем,	считая произвольную постоянную C

функцией, зависящей от x , общее решение полного (неоднородного) уравнения отыскивают

виде

y C (x) exp Pdx . Подставляя

y(x) в (6.1),

получим уравнение для

C (x) :

(x)exp P(x)dx Q .

Пример 6.1.9. Найти решение задачи Коши

x / 1

y(e) 0 .

y x ln x y

Решение. Будем искать общее

решение

уравнения в виде y U (x)V (x) ,

тогда

. Подставляя выражения для y

и y

в уравнение, получим

U V UV

x ln xVU xV ln x V U 2x2 ln2

x / 1 x2 .

(6.2)

Функцию V находим из условия xV ln x V 0 . Тогда имеем

ln x

V C ln x .

x ln x

V ln x C 1 , и подставляя его в (6.2),

Выбирая любое частное решение, например,

получим уравнение для U (x) : x ln2 xU 2x2

ln2 x / 1 x2 .

160

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 1516 / 2816 17 18 19 20 21 22 23 24 25 26 27 28 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.02.201581.23 Кб168.docx
#
20.09.2019105.47 Кб18_beR.doc
#
07.02.2015282.72 Кб399-105.docx
#
06.02.2015219.14 Кб17Abl_BH_Met_Flash.doc
#
06.02.201526.62 Кб14about_myself_1.doc
#
07.02.20152.14 Mб36Ankilov.pdf
#
18.11.2019159.23 Кб3Arkhivovedenie-1.doc
#
13.08.2019157.18 Кб3B7.doc
#
20.12.2018451.58 Кб21Batychko_V_T_Trudovoe_pravo_v_voprosah_i_otveta....doc
#
26.04.2019304.13 Кб2bilety_po_yazykoznaniyu_Vosstanovlen.doc
#
05.08.201967.37 Кб2Bilet_ps.docx