48. Функция. Способы задания функции. Классификация функций.

Функция — соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу одного множества ставится в соответствие некоторый элемент из другого множества.

Наиболее частые способы задания функции:

1. Аналитический Функция задается в виде одной или нескольких формул или уравнений. Наиболее совершенный способ. К нему приложены методы мат. анализа, позволяющие исследовать функцию .

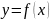2. Табличный Функция задается таблицей ряда значений аргумента и соответствующих значений функции.

3. Графический Задается график функции.

Классификация.

Функции, заданные аналитически, подразделяются на два класса: алгебраические и трансцендентные. Алгебраическими называются функции, значения которых получаются в результате выполнения над значениями аргумента конечного числа алгебраических действий (сложении, умножения, деления, возведения в степень и извлечения корня). Например, .

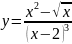Функция, не являющаяся алгебраической, называется трансцендентной (например, ).

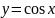49. Числовые последовательности. Свойства.

Под числовой последовательностью 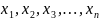понимается функция

,

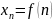заданная на множестве 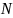натуральных чисел. Кратко последовательность обозначается 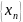или .

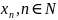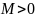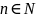Последовательность называется ограниченной, если существует такое число , что для любого выполняется неравенство

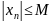
В противном случае последовательность называется неограниченной.

Последовательность называется возрастающей (неубывающей), если для любого выполняется неравенство 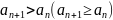. Аналогично определяется убывающая последовательность.

Если все элементы последовательности равны одному и тому же числу, то её называют постоянной.

Чаще всего последовательность задается формулой его общего члена. Формула позволяет вычислить любой член последовательности по номеру n, по ней можно сразу вычислить любой член последовательности. (Например, ).

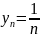Другой способ задания числовых последовательностей – рекуррентный способ. В нем задается начальный элемент 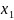(первый член последовательности) и правило определения n-го элемента по (n-1)-му:

.

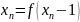50. Бесконечно-малые, бесконечно большие последовательности.

Последовательность называется бесконечно большой, если для любого числа A>0 существует такой номер 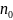, начиная с которого (то есть для всех 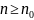) выполняется соотношение .

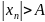Замечание. Различие между бесконечно большой и неограниченной последовательностью в том, что в случае бесконечно большой последовательности соотношение   должно выполняться для всех  , а для неограниченности последовательности достаточно, чтобы существовал хотя бы один элемент последовательности, для которого выполняется  .

Следствие. Любая бесконечно большая последовательность является неограниченной (но не наоборот).

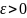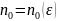Последовательность   называется бесконечно малой, если для любого числа   существует такой номер  , начиная с которого ( ) выполняется соотношение  .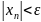

Замечание. Любая бесконечно малая последовательность является ограниченной, но не наоборот.