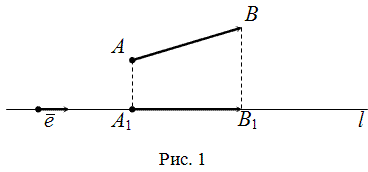
13. Единичные векторы (орты). Проекции вектора на ось. Разложение вектора по осям (по базису).

Единичный вектор или орт — вектор, длина которого равна единице. Проекцией вектора 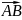  на ось   называется длина отрезка  , взятая со знаком "+", если направление 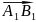  совпадает с направлением вектора 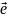 , и со знаком "-", если направление    противоположно направлению единичного вектора оси  .

Проекция вектора   на ось  обозначается символом  .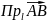

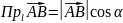
Разложение вектора по базису

Пространство 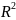(плоскость)

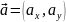
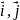– единичные векторы, сонаправленные осям 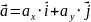– разложение вектора по ортам (по прямоугольн. базису)

Пространство

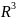
Oy – ось ординат

Оx – ось абсцисс

Oz – ось аппликат

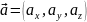
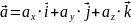- разложение по ортонормированному базису 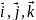– орты

Теорема Если даны два линейнонезависимых вектора и , то любой третий вектор на плоскости может быть представлен в виде разложения по базису, образованному векторами на плоскости.

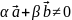
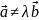
|| (не параллельны)

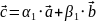
Теорема

Если даны три линейнонезависимых вектора в пространстве: 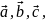то любой четвертый вектор 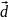может быть разложен по базису этих трёх векторов и при чем единственным образом.

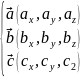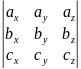
Если 0, то 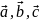– линейнонезависимы, т.е. образуют базис

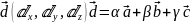
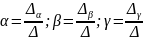
14. Компланарные векторы. Длина вектора. Направляющие косинусы и их свойства.

Векторы, которые параллельны одной плоскости или лежат на одной плоскости, называются компланарными векторами. Тот же смысл имеет и другое определение: Три вектора называются компланарными, если они, будучи приведёнными к общему началу, лежат в одной плоскости.

Длина вектора (модуль) – неотрицательное число, равное расстоянию между его началом и концом. Длина обозначается .

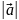Длина вектора, заданного координатами, равно квадратному корню из суммы квадратов его координат.

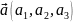
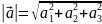
Направляющие косинусы

Направляющие косинусы вектора   – это косинусы углов, которые вектор образует с положительными полуосями координат. Направляющие косинусы однозначно задают направление вектора.

Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора.

В случае плоской задачи направляющие косинусы вектора 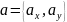 можно найти воспользовавшись следующей формулой

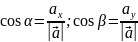
В случае пространственной задачи направляющие косинусы вектора 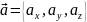 можно найти воспользовавшись следующей формулой

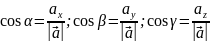
Свойство: Сумма квадратов направляющих косинусов = 1.

15. Действия над векторами, заданными своими проекциями. Проекция вектора на вектор.

Пусть даны два вектора  и  , заданные своими проекциями: или

или 

Укажем действия над этими векторами. 1.Сложение: или, что то же , т.е. при сложении двух векторов одноимённые координаты складываются. 2.Вычитание: или, что то же , т.е. при вычитании двух векторов одноимённые координаты вычитаются. 3.Умножение вектора на число: или, что то же , т.е. при умножении вектора на число все координаты умножаются на это число.

Проекция вектора на вектор

Проекция вектора на вектор обозначается =

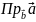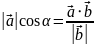
16. Основные теоремы о проекциях.

Теорема 1. Проекция суммы векторов на какую-либо ось равна сумме проекций слагаемых векторов на ту же ось.

Теорема 2. Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:

Теорема 3. Если вектор  умножается на число, то его проекция на ось также умножается на это число:

17. Скалярное произведение и его свойства.

Скалярным произведением двух векторов и называется число равное произведению длин этих векторов на косинус угла между ними.

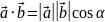
Скалярное произведение на = сумме произведений одноименных координат.

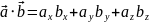
Свойства скалярного произведения:

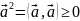1. , при чем

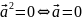
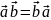2. (переместительный закон)

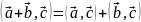3. (распределительный закон)

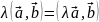4. (сочетательный закон)

18. Угол между векторами.

Угол между векторами — угол между направлениями этих векторов (наименьший угол).

Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.

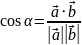
19. Векторное произведение и его свойства.

Векторным произведением и называется , координаты которого находятся по формуле:

=

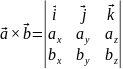Свойства векторного произведения:

1. 

2. 

3. 

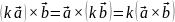
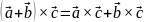
4. Вектор  , равный векторному произведению не нулевых векторов   и  , перпендикулярен этим векторам.

5. Векторное произведения двух не нулевых векторов   и   равно нулю тогда и только тогда, когда вектора коллинеарны.

6. Модуль векторного произведения двух векторов  и  равен площади параллелограмма построенного на этих векторах:

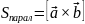
7. Площадь треугольника построенного на векторах   и  равна половине модуля векторного произведения этих векторов: