81. Теорема Лагранжа. Геометрический смысл.

Теорема Лагранжа. (О конечных приращениях)

Пусть функция 

1. непрерывна на отрезке  ;

2. дифференцируема на интервале  .

Тогда на интервале   найдется по крайней мере одна точка  , такая, что

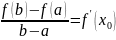
(Геометрический смысл теоремы Лагранжа)

На кривой   между точками   и   найдется точка 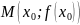, такая, что через эту точку можно провести касательную, параллельную хорде  .

Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде:

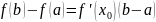
 Теорема Лагранжа является частным случаем теоремы Коши при .

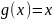82. Теорема Коши. Геометрический смысл.

Теорема Коши. (Об отношении конечных приращений двух функций)

Если функции   и  :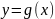

1. непрерывны на отрезке  ;

2. дифференцируемы на интервале  ;

3. производная 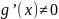  на интервале  ,

тогда на этом интервале найдется по крайней мере одна точка  , такая, что

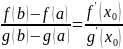
Теорема. Если производная функции равна нулю на некотором промежутке, то функция является постоянной на этом промежутке.

Теорема. Если две функции имеют равные производные на некотором промежутке, то они на этом промежутке отличаются друг от друга на некоторое слагаемое.

(Геометрический смысл теоремы Коши)

Пусть плоская кривая γ описывается параметрическими уравнениями 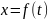 ,  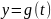, где параметр   изменяется в промежутке  . При изменении параметра   точка кривой на рисунке 1 пробегает от 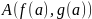  до 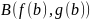 . В соответствии с теоремой Коши на кривой 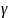  найдется точка 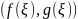 , в которой касательная параллельна хорде, соединяющей концы   и   данной кривой. 

83. Правило Лопиталя.

Правило Лопиталя распространяется на случай неопределенности типа   при  .

(Правило Лопиталя).

Пусть функции   и  удовлетворяют следующим условиям:

1) эти функции дифференцируемы в окрестности точки  , кроме, может быть, самой точки  ;

2) 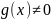  и   в этой окрестности;

3)  ;

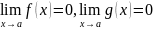4) 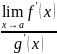  существует конечный или бесконечный.

Тогда существует и 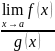  , причем  .

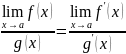Правило Лопиталя распространяется и на случай  . Чтобы убедится в этом, достаточно сделать замену 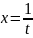  и воспользоваться результатом выше приведенной теоремы.

84. Признаки постоянства и монотонности функции.

Признак постоянства.

Необходимое и достаточное условие постоянства функции выражается равенство .

Признак монотонности.

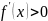
Если функция дифференцируема на интервале и 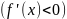для 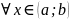, то эта функция возрастает (убывает) на интервале .

(Функция возрастающая или убывающая называется монотонной).

85. Экстремум функции. Необходимое условие существования экстремума.

Точка   называется точкой локального максимума функции  , если существует такая окрестность этой точки, что для всех   из этой окрестности выполняется неравенство:  .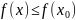

Точка   называется точкой локального минимума функции  , если существует такая окрестность этой точки, что для всех   из этой окрестности  .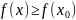

Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.

Замечание. Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.

(Необходимое условие экстремума)

Если функция   имеет экстремум в точке  , то ее производная 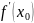  либо равна нулю, либо не существует.

Точки, в которых производная равна нулю: 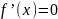 , называются стационарными точками функции.

Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки - это либо стационарные точки (решения уравнения  ), либо это точки, в которых производная 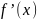  не существует.

Замечание. Не в каждой своей критической точке функция обязательно имеет максимум или минимум.