Билеты по математике

1. Матрицы. Действия над матрицами.

Матрица – таблица чисел. Обозначение: 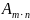, где m-число строк, n-число столбцов. Обозначение элемента: 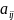, где i-номер строки, j-номер столбца.

Возможные действия над матрицами:

-Умножение на число;

Каждый элемент матрицы умножается на это число.

-Сложение двух матриц;

Только для матриц одинаковой размерности. Складываются соответствующие элементы.

-Умножение двух матриц.

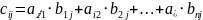
Квадратная матрица – матрица с одинак. кол-вом строк и столбцов.

Единичная матрица – матрица, у которой по главной диагонали стоят единицы, а остальные – нули.

2. Определители 2-ого и третьего порядка.

Обозначение – detA, или |A|, или Δ. detE=1

Определитель второго порядка:

=

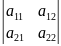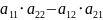
Определитель третьего порядка:

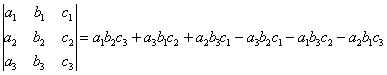
Или:

3. Основные свойства определителей второго и третьего порядка. (миноры, алгебраические дополнения).

• Постоянный множитель из любого ряда может быть вынесен за знак определителя.

• Если в detA поменять местами два параллельных ряда, то знак detA изменится на противоположный.

• Определитель матрицы, содержащей нулевой ряд = 0.

• К элементам любого ряда опр-ля можно прибавить соответствующие эл-ты параллельного ряда, умноженные на одно и то же число. При этом величина detA не изменится.

• Определитель с двумя равными строчками = 0.

• Определитель с двумя пропорциональными строчками = 0.

• При транспонировании матрицы величина определителя не меняется.

• Определитель = сумме произведений эл-ов любого ряда на соответствующие этим элементам алгебраические дополнения.

Алгебраическое дополнение:

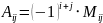
Где M – минор матрицы. (Определитель матрицы (n-1) порядка, полученный из матрицы A вычеркиванием i-ой строки и j-столбца).

4. Определители высших порядков. Свойства. Методы вычисления.

Определитель высших порядков решается с помощью последнего свойства: «Определитель = сумме произведений эл-ов любого ряда на соответствующие этим элементам алгебраические дополнения.»

Пример разложения определителя по первой строке:

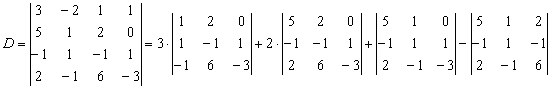
5. Теорема Крамера. Решение системы с помощью определителей.

Теорема Крамера. Если определитель матрицы квадратной системы не равен нулю, то система совместна и имеет единственное решение, которое находится по формулам Крамера:

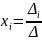
где   - определитель матрицы системы,   - определитель матрицы системы, где вместо   -го столбца стоит столбец из правой части системы уравнения.

6. Обратная матрица.

Обратно матрицей называется такая матрица 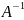, при умножении на которую исходная матрица A даёт в результате единичную матрицу.

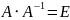
Метод нахождения обратной матрицы:

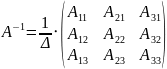
(транспонированная матрица алгебраических дополнений)

транспонированная матрица - матрица, в которой строки и столбцы поменяли местами.

7. Матричный способ решения систем уравнений.

Метод обратной матрицы.

Столбик из x находится с помощью формулы

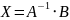
где – обратная матрица, B – матрица из правой части системы уравнения, X - матрица из x.

Т.е. для системы уравнений:

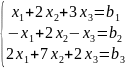
B=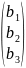 , X= . .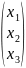

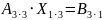Алгоритм решения системы уравнения методом обратной матрицы:

1. Найти определитель матрицы.

2. Найти все алгебраические дополнения

3. Найти обратную матрицу по формуле из 6 вопроса

4. Умножить обратную матрицу на матрицу B.