2. Исследование влияния параметров на устойчивость системы

Исследование проводится методом D – разбиений, и область устойчивости строится в плоскости двух задаваемых параметров системы: постоянная времени объекта управления T_об и коэффициент усиления объекта k_об. Для выполнения исследования необходимо найти характеристический комплекс системы. Для этой цели характеристический полином системы преобразуется таким образом, что вместо числовых значений исследуемых параметров в него бы вошли их буквенные обозначения:

(2.8)

Характеристический полином преобразуется в характеристический комплекс подстановкой p=jω[1]:

G(jω) = -T_об∙ω²+jω + k_об∙7.695 (2.9)

Условия для граничной устойчивости системы:

(2.10)

Полученные уравнения решаются относительно исследуемых параметров:

(2.11)

при ω=0: k_об=0, T_об=∞,

при ω=∞: k_об=∞, T_об=0.

Используем условия устойчивости: C₀=0 и C₂=0, откуда: T_об=0 и k_об=0.

Определяется расположение области устойчивости относительно границ с использованием правила штриховки, для этого составляем определитель[1]:

==0 (2.12)

Область устойчивости – первая четверть (рис. 8).

Рис. 8 Область устойчивости

Для проверки построений на графике нанесем точку (k_об,Т_об) (зависящие от ω). Примем точку А с координатами (2.3; 0,04); точка принадлежит полученной области устойчивости, следовательно область устойчивости построена верно.

2.2 Исследование качества системы

2.2.1 Уравнение переходного процесса в системе

Передаточная функция замкнутой системы[2]:

Ф(р) = (2.13)

где: А(р) и С(p) – степень полинома от p, тогда дифференциальное уравнение системы в операторной форме будет иметь вид:

С(p)·y(p) = A(p)·x(p) (2.14)

где: р - оператор дифференцирования; y(p)- выходной сигнал системы; x(t)- входное воздействие.

Входным воздействием принимается единичная ступенчатая функция x(t) = 1(t), А(р) принимаем равным k_c. Тогда уравнение системы (2.14) примет следующий вид:

(0.04p²+p+17.7)∙y(t)=17.7∙х(t) (2.15)

2.2.2. Построение графика переходного процесса

Построение графика переходного процесса в системе по средствам программной среды MathCAD. Так как исходное уравнение имеет вид (2.15), то дифференцирование входного сигнала x(t)=1(t) в правой части уравнения приведет к бесконечно большой величине, что повлечет за собой ошибку в программной среде. Чтобы решение уравнения стало возможным, структуру системы следует преобразовать в виду, показанному на рис. 9. Такое преобразование приводит к тому, что исходное уравнение (2.15) распадается на два уравнения (2.16)[1]:

Рис.9 Преобразованная структура системы

Новой структуре соответствует система уравнений:

(2.16)

Первое уравнение является дифференциальным, второе – алгебраическим, так как содержит производные, находимые из первого уравнения.

Для построения графика переходного процесса (рис. 10) необходимо решить дифференциальное уравнение:

(2.17)

При численном решении дифференциального уравнения n-го порядка преобразуем в систему из n уравнений первого порядка. Для этого выполняем подстановку вида:

z(t)=z₁(t), z^’(t)=z₂(t) (2.18)

В результате подстановки можно записать систему уравнений следующего вида:

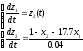(2.19)

Для решение системы в MathCAD необходимо указать следующие параметры:

Исходное уравнение:

(2.20)

Решение дифференциального уравнения методом Рунге-Кутта:

Z:= rkfixed(x,0,20,2000,D) (2.21)

гд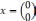е: - начальные условия,n – 2000 число точек решения; tk = 200 конечное время решения, D – исходное уравнение.

Конечный результат для вычисления переходного процесса:

Y:=17.7Z^<1> (2.22)

Найденные значения представлены в таблице 1. Расчет точек для графика переходного процесса представлен в таблице 2.

Таблица 1. Расчет точек переходного процесса

Таблица 2. Расчет точек для графика переходного процесса

Рис. 10 График переходного процесса системы