1.9. Кері тор. Кері тордың қасиеттері. Бриллюэн зонасы. Вигнер-Зейтц ұяшығы. Кері тор.

Вигнер-Зейтц ұяшығы. Анықтама бойынша примитивті ұяшық бұл минимальді көлемді ұяшық. Кристалдың бір примитивті ұяшығына тордың тек бір түйіні ғана сәйкес келеді. Примитивті ұяшық Вигнер-Зейтц ұяшығы түрінде жиі кездеседі. Вигнер-Зейтц ұяшығын құру келесідей болады: тордың бір түйіні таңдалып алынады, осы түйінді басқа көрші түйіндермен жалғайтын сызық жүргізіледі. Құрылған сызықтың ортасы арқылы оған перпендикуляр жазықтық жүргізіледі. Осы жазықтықпен шектелген фигура Вигнер-Зейтц ұяшығы болып табылады.

Кері тор. Рентгенді дифракцияда кері тор ұғымы қолданылады. Кері тордың негізгі (базисті) векторлары төмендегі теңдеулермен анықталады:

; ;

Мұнда векторлық алгебрада төмендегі қатынас орындалатындығы көрсетілген:

= =

Алымында тұрған шама қарапайым ұяшықтың көлемін көрсетеді.

Кері торлардың бұрыштық параметрлері мына теңдеумен анықталады:

; ; .

Кері тордың трансляция векторы:

,

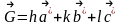мұндағы h,k,l –бүтін сандар.

Кері тордың трансляция векторының тура тордың трансляция векторына көбейтіндісі:

бүтін сандар

Кристаллографтар әдетте көбейткішін түсіріп тастайды, бірақ конденсирленген күй физикасымен айналысатын физиктердің көпшілігі осы көбейткішті қалдырады.

Әрбір кристалдық құрылымға екі тор: кристалдық тор және кері тор сәйкес келеді. Олар жоғарыда көрсетілген қатынастармен тығыз байланысты. Кристалдың рентгендік дифракциялық суреті кері тордың картасын берсе, микроскопиялық суретте кристалдың нақты құрылымының картасын дәл солай береді деуге болады. Кристалдық тор векторының ұзындық өлшемі болса, кері тор векторының шамасы [ұзындық]^-1.

Кристалдық тор – бұл әдетте нақты кеңістікте кездеседі, ал кері тор – бұл Фурье кеңістігіндегі тор. Бриллюэннің бірінші зонасы ол кері тордағы Вигнер-Зейтц ұяшығы.

Кері тордың көмегімен кристаллографияның көптеген міндеттері жеңіл шешіледі. Кристаллографиялық есептеулерде жиі кездесетін бірнеше теңдеулерге мысал келтірейік. (hkl) жазықтығы сериясы үшін жазықтықтар арасындағы қашықтықтар мына теңдеу арқылы анықталады:

векторының ұзындығы мына формуламен есептеледі: . Осылай гексагоналді сингония үшін:

,

мұндағы . Кубты тор үшін:

.

1.10. Бриллюэн зонасы

Тура тордың периоды a болсын делік. Кері тор ұғымы периодты функцияның жазық толқындарға үлестірілуінен туындады. Бірөлшемді жағдайда периодты функцияның Фурье қатарына үлестірілуі мына түрде болады:

(1.1)

Осылайша, бірқалыпты жағдайда кері торды G_n=2πn/a нүктелері құрады, бұл нүктелер кері тордың векторларының рөлін атқарады. Жеңіл болу үшін біріншіден, бірөлшемді торды және бірөлшемді Бриллюэн зонасының құрылуын қарастырамыз. Бриллюэн зоналары келесі түрде құрылады: кері торда түйіндерді қосатын кесінділердің ортасына нүкте қойылады. Бірінші зона — [–π/a,π/a] кесіндісі, екіншісі — бірінші зонаны алып тастандағы [–2π/a,2π/a] кесіндісі, және т.с.с. (18-сурет)

1.20-сурет. Бірөлшемді жағдайдағы Бриллюэн зонасы.

1.21-суретте екіөлшемді тікбұрышты кері тор үшін Бриллюэннің төрт зонасы бейнеленген. Олар бірөлшемді жағдайдағыдай құрылады, тек нүктелердің орнына түзу сызықтар жүргізіледі.

Үшөлшемді тор үшін Бриллюэн зонасы ослай құрылады тек түзулердің орнына жазықтықтар жүргізіледі. Осылай анықталған жазықтықтар класы, координаталар басымен қосылған кері тордың түйіндерінің жан-жағын көпжақты пішіні бар қандай да бір көлеммен шектейді. Қарапайым кубты тор жағдайында көпжақты куб болып табылады. Оның қырлары осы тордың түйіндерін басқа көрші түйіндерімен қосатын векторлардың ортасы арқылы өткізілетін жазықтармен құрылған. Барлық басқа жазықтар түйіннен алшақ өтеді және кубтың қырларының құрылуына өз үлесін қоспайды. Көлемді-центрленген кубты тор жағдайында күрделі көпжақтылар құрылады (төменді қара). Оның қырлары берілген түйін мен оның жақын бірінші және екінші көршілері арасынан өткізілген жазықтармен құрылады. Құрылған көпжақтылар Бриллюэннің бірінші зонасы деп аталады. Егер барлық жазықтардың бірігуінен Бриллюэннің бірінші зонасының қырларын алып тастасақ, онда қалған көптік координата басы айналасында жаңа көпжақтының құрылуын шектейді. Бриллюеннің бірінші зонасына кірмейтін осы көптіктің жартысы Бриллюэннің екінші зонасын түзеді. Келесі қадамда біз Бриллюэннің үшінші зонасын аламыз және т.с.с.

1.21-сурет

Бриллюэннің бірінші зонасын нүктелік симметриясы бар, кері тордың примитивті ұяшығы ретінде қарастыруға болады. Расында да, егер кері тордың әр түйінінің жанына Бриллюэннің бірінші зонасын құрсақ (координаталар басын осы түйінге орналастырсақ), онда осы зоналар бір-бірімен беттеспей барлық кеңістікті толығымен толтырады. Мұнда Бриллюэннің бірінші зонасының көлемі кері тордың примитивті ұяшығының көлеміне тең болатындығын көруге болады.

Бриллюэннің кейбір қасиеттері:

Бриллюэннің барлық зоналарының көлемдері бірдей және кері тордың примитивті ұяшығының көлеміне тең.

Бриллюэннің барлық зоналары бірінші зонаның репликасы болып табылады: оларды бірінші зонаға жататын нүктелерін кері тор векторына трансляциялау арқылы алуға болады.

1.22-сурет

Жартылайөткізгіштердің кең таралған түрлерінің көпшілігінің торлары қырға центрленген кубты (ГЦК) Браве торларына жатады, осы тордың Бриллюэннің бірінші зонасы қалай орналасқанын қарастырайық. Мұндай жағдайда кері тор көлемді центрлі кубты (КЦК) болып табылады. Бриллюэннің бірінші зонасы 1.22-суретте бейнеленген. Жоғарыда көрсетілген алгоритмге сәйкес ол келесідей болады. Бірінші кубты, қарапайым ұяшықтың центріндегі түйін мен оның екінші көршісінің арасын қосатын түзуді екіге бөлетін жазықтық жүргіземіз. Бұл жазықтықтар кубты ұяшықтармен сәйкес келетін, орталық түйіннің жан жағындағы кубты шектейді. Осы кубтың бұрыштарында орталық түйіннің жақын көршілері орналасқан. Осы көршілері мен орталық түйіндері арасынан жүргізілетін жазықтықтар кубпен қиылысқан кезде алтыбұрышты қырларды түзеді, ал кубтың қырларынан квадраттарды ''қиып '' алады.

ГЦК-торда Бриллюэннің бірінші зонасының кейбір жоғары симметриялы нүктелері мен сызықтарының жалпыға бірдей белгіленулері бар. Бриллюэн зонасының центрі грек әрпімен белгіленеді Γ. Жазықтық бетіндегі нүктелер латын әріптерімен белгіленеді: X — квадрат қырының центрі (k-жазықтығындағы (1,0,0) бағыты және оған эквивалент барлығы 6 нүкте); L — алтыбұрышты қырдың центрі ((1,1,1) бағыты және оған эквивалент барлығы 8 нүкте); K — көрші алтыбұрышты қырлардың арасындағы қабырғалардың ортасы ((1,1,0) бағыты және оған эквивалент барлығы 12 нүкте). Зона центрі мен жазықтық бетіндегі нүктелерді қосатын сызықтар грек әріптерімен белгіленеді: Γ X — Δ ((1,0,0) түріндегі бағыт), ΓL — Λ ((1,1,1) түріндегі бағыт), Γ K - Σ ((1,1,0) түріндегі бағыт).