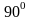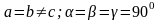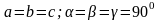- •1.Бөлім. Идеал кристалдардың геометриясы
- •Монокристалдар. Поликристалдар
- •1.2. Кристалдың трансляциялық симметриясы. Негізгі векторлар
- •1.3. Нүктелік симметрияның элементтері және түрленуі
- •1.4.Бөлім. Топтар теориясы. Топтарды анықтау
- •1.5. Симметрия топтарына мысалдар
- •1.6. Кристалдың кеңістікті симметриясы
- •1.7. Кристалографиялық индицирлеу әдісі. Бүтін сандар заңы.
- •1.8. Қарапайым кристалдық құрылымдар
- •1.9. Кері тор. Кері тордың қасиеттері. Бриллюэн зонасы. Вигнер-Зейтц ұяшығы. Кері тор.
- •1.10. Бриллюэн зонасы
- •2. Бөлім. Толқындардың конденсирленген ортамен әсерлесуі
- •2.1. Кристалдардың құрылымын зерттеу үшін қолданылатын электромагнитті толқындар
- •2.2. Кристалдық торға түсетін рентгендік сәулелердің дифракциясы
- •2.3. Лауэ теңдеуі. Эвальдо түзілімі
- •2.4. Шашыраған (дифракцияланған) толқын амплитудасы үшін Лауэ теңдеуі
- •3.Бөлім. Кристалдардағы ақаулар
- •3.1. Нүктелік ақаулар
- •3.2. Сызықтық ақаулар
- •3.3. Беттік және көлемдік ақаулар
- •4. Бөлім. Байланыс типі бойынша қатты денелердің классификациясы
- •4.1. Конденсирленген күйдегі молекулалар және атомдар арасындағы әсерлесу күштерінің типтері. Байланыс энергиясы.
- •4.2. Инертті газ кристалдары
- •4.3. Ионды кристалдар
- •5. Бөлім. Қатты денелердің жылулық қасиеттері. Кристалдық тордың тербелісі.
- •5.1. Дюлонг-Пти заңы. Фонон.
- •5.2. Фонондарды тәжірибелік зерттеудің әдістері
- •5.3. Кристалдық тордағы атомдардың тербелісі
- •5.4. Кристалдардың жылусыйымдылығы
- •6. Бөлім. Қатты денелердің электрлік қасиеттері
- •6.1. Қатты денелердегі электрондық күйлер
- •6.2. Диэлектриктер, жартылай өткізгіштер және өткізгіштер
- •6.3. Өткізгіштің электр өтімділігі
- •6.4. Жартылай өткізгіштің электр өтімділігі
- •7. Бөлім. Қатты денелердің механикалық, оптикалық және магниттік қасиеттері
- •7.1. Физикалық тензорлар
- •7.2. Гук заңы. Серпімді модульдердің тензоры
- •7.3. Кубты кристалдар үшін серпімді тұрақтыларды есептеу
- •7.4. Кубты кристалдардағы серпімді толқындар
- •8.Бөлім. Кристалл емес қатты денелер. Сұйық кристаллдар
- •8.2. Аморф заттардың қасиеттері
- •8.3. Аморф жартылай өткізгіштер
- •8.4.Заттың сұйық күйі. Сұйықтардың қасиеттері. Сұйық кристаллдар
- •8.2 Сурет - Сұйықтың аз көлемінің тамшыға айналу (а) және жұғатын (б) және жұқпайтын (в) беттермен мениск жасау қасиеті.
- •8.3 Сурет - Смектикалық типті сұйық кристаллдың
- •8.4 Сурет - Нематикалық типті сұйық кристаллдың құрылысы
- •8.5 Сурет - Холестерикалық типті сұйық кристаллдың құрылысы
- •9. Наноматериалдар
- •9.1 Наноматериалдарды жіктеу негіздері және құрылымдарының типтері
- •9.1 Сурет - Наноматериалдар ұғымының терминологиялық тәсілдері
- •9.2. Наноматериалдар қасиеттерінің ерекшеліктері
- •9.3 Фуллерендер, фуллериттер, нанотүтіктер
- •9.4 Сурет - Фуллерен молекулалар: а) c60, б) c70,
- •9.4. Кванттық шұңқырлар, кванттық өткізгіштер, кванттық нүктелер
- •Қазіргі уақытта наноматериалдар мен нанотехнологияларды қолданатын негізгі салалар
- •9.8 Сурет - Наноматериалдарды қолдану мысалдары
- •9.9 Сурет - Fe0,3Co0,7 құймасынан диаметрі 50 нм наноөткізгіштер: а) наноөткізгішті төсеніштің жоғарыдан көрінісі, б) өткізгіштердің түрі.
- •Атомдық жазықтықтардың дұрыс кезектесуінің бұзылуын сипаттайтын кристалдық тордың сызықтық ақауы.
- •Әдебиеттер тізімі
- •Мазмұны
1.6. Кристалдың кеңістікті симметриясы
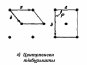
Осыған дейін біз симметрияның түрленуінің екі типін қарастырып келдік: трансляция және нүктелік түрленулер. Трансляцияға қатысты симметрия — кристалдың басты қасиеті. Оны толықтай Бравэ торы айшықтайды (2, 3-кестелерді, 1.9,1.10-суреттерді қара).
2-кесте. Бес екі өлшемді Бравэ торлары
Торлар |
Қарапайым ұяшық |
Симметрияның нүктелік тобының халықаралық көрсеткіші |
Қиғаш бұрышты |
Параллелограмм
|
2 |
Квадратты |
Квадрат,
|
4mm |
Гексагональді |
|
6mm |
Тікбұрышты |
Тікбұрышты,
|
2mm |
Центрленген тікбұрышты |
Тікбұрышты,
|
2mm |
mm көрсеткіші екі жазықтықтың айналы шағылысуы бар екендігін көрсетеді
3-кесте. Он төрт кеңістікті Бравэ торы
Кристаллографиялық жүйе (сингония) |
Жүйедегі ұяшық саны |
Ұяшық символы |
Элементар ұяшықтың сипаттамасы |
Триклинді |
1 |
P |
|
Моноклинді |
2 |
P, C |
|
Ромбты |
4 |
P, C, I, F |
|
Тетрагоналді |
2 |
P, I |
|
Кубты |
3 |
P, I, F |
|
Тригоналді |
1 |
R |
|
Гексагоналді |
1 |
P |
|
Суретте көрсетілген қарапайым ұяшықтардың барлығы примитивті емес. С - бұл центрлі негізі бар болатын ұяшық, I - көлемді-центрленген ұяшық, F- қырға центрленген ұяшық.
3-кестеде торлардың типтері, ал 12-суретте он төрт кеңістікті Бравэ торлары көрсетілген .
|
|
|
|
1.11-сурет. Бес екіөлшемді Бравэ торы
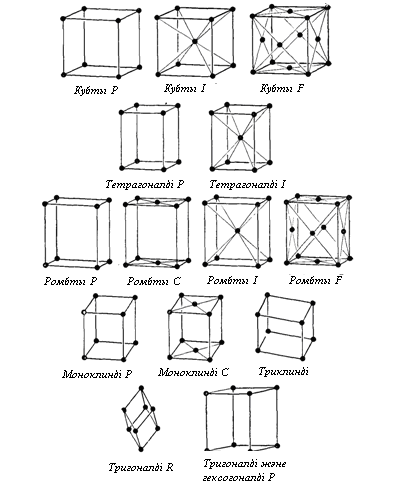
1.12-сурет. Он төрт кеңістікті Бравэ торлары
Браве торының симметриясы нүктелік түрленулерге қатысты сингония немесе кристалды жүйе деп аталады. Түрлі сингонияны сипаттайтын симметрияның барлығы 7 тобы бар (3-кесте), яғни 7 түрлі топтың әрқайсысында нақты бір Бравэ торының симметрияның барлық нүктелік түрленулері болады. Кристалл трансляциялық симметриясын толықтай анықтайтын Бравэ торымен ғана емес, сонымен қатар базиспен, яғни примитивті ұяшықтың түзілуімен (примитивті ұяшықты құратын атомдардың типтері мен келісімді орналасуы) де сипатталады. Бравэ торының әр түйініне бір атом сәйкес келетін, қарапайым кристалл симметриясы Бравэ торының сингониясымен сәйкес келеді. Ал күрделі кристалға келетін болсақ, онда оның нүктелік симметриясы Бравэ торының симметриясынан жоғары бола алмайды. Осылайша, жалпы жағдайда кристалдың нүктелік симметриясының тобы оның Бравэ торының (сингония) симметрия тобының топшалары болып келеді. Осындай топшаларды, яғни трансляциялық симметриямен сәйкес келетін нүктелік симметрия тобы 32 – ге жетеді.
Мысалы, Oh кубының симметрия тобының (кубты сингония) бес топшасы бар, оның ішінде біз қарастырған үш топтар да бар: Oh, O, Td.
Нүктелік түрленулер мен трансляциялар кристалдық тор симметриясының түрлену жиынын жояды (олар Бравэ торының симметриясының түрленуін де жояды).
Кристалдық торлардың қосымша симметрия элементтері де бола береді:
n-ші ретті бұрандалы өстер. Сәйкес түрленулер бұрыштарға бұрылуға және дәл осы оспен pa/n арақашықтығына жеткізілуіне негізделген. Мұнда p=1,2,...,n–1; a — нақ осы осьтегі ең аз период.
Айналы сырғу жазықтығы. Сәйкес түрленулер ось бойымен жүретін трансляцияның нақ сол жазықтықта a/2 арақашықтықта жататын осы жазықтыққа шағылысуына негізделген.
Кристалдың кеңістікті симметрия тобы кристалдық тордың симметриясының барлық түрленулерін қамтиды: трансляция, нүктелік түрленулер, бұрандалы өстер мен айналы сырғу жазықтығына байланысты түрленулер (кристалдық тордың симметриясының басқа түрленулері болмайтындығын көрсетуге болады). Симметрияның барлық кеңістікті топтары XIX ғасырдың аяғында Е.С.Федоровпен табылған. Олардың саны 230.

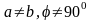
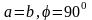
 -градусты
ромб,
-градусты
ромб,

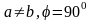
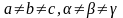
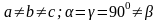
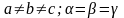 =
=