1.5. Симметрия топтарына мысалдар

Тең қабырғалы үшбұрыштың симметрия тобы.

Тең қабырғалы үшбұрыш – симметриялы фигура. Топтар теориясы осы фигура симметриясын сипаттауға, барлық симметрия түрленулерін анықтауға мүмкіндік береді. Егер үшбұрышты жазықтықтан шығармасақ, онда ол келесідегідей симметрия элементтерін қамтиды (1.8–сурет, сол жағы):

1.8-сурет. Тікбұрышты үшбұрыштың симметрия тобы

Үшінші ретті симметрия өсі (үшбұрыш ортасы арқылы, жазықтыққа перпендикуляр): үшбұрыш өз жазықтығынан 120^° бұрышқа (L₃ түрленуі) және 240^° бұрышқа (L₃² түрленуі) айналады. Симметрияның үш жазықтығы, бұл жазықтықтар үшінші ретті симметрия осі арқылы өтеді, сондықтан олар P_v арқылы белгіленеді.

3.Түйіндес түрлендірулер.

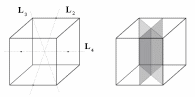
Сонымен: L₃, L₃², P₁, P₂, P₃, E бар делік. Аталған түрленулер топты құру керек, яғни кез-келген екі элементтердің көбейтіндісі осы топтың элементін беруі керек. Сондықтан симметрияның түрленуінің жиынтығы үшін көбейту кестесін құруға болады. Тікбұрышты үшбұрыш симметриясының түрлену топтарына көбейту кестесін құру үшін қандай да бір симметрия элементінде жатпайтын нүкте алып, оған тізбектей барлық түрленулер мен түрлену туындыларын қолданайық. 1.8-суретте (үшбұрышта, оң жағы) бастапқы нүкте E арқылы белгіленген — ұқсас түрленулер, басқа нүктелер —L₃ өсін айнала бұрылудың нәтижесі, кресттер — симметрия жазықтығынан шағылу нәтижесі. Осы суретті пайдалана отырып, көбейту кестесін құруға болады. Мысалы, P₃P₂ көбейтіндісін табу керек. σ₂ нүктесі суретте бар. Оны σ₃ шағылуа душар ету керек. Нәтижесінде L₃ нүктесіне келеміз. Осылайша, P₃P₂=L₃.

Осылай әрекет ету арқылы, тікбұрышты үшбұрыш симметриясының тобы C_3v үшін көбейту кестесін аламыз (1–кесте; көбейту коммутативті болмағандықтан, көбейту ретін анықтау керек: бірінші сол бағанадан түрлену алынады, кейін – үстіңгі қатардан алынады).

1-кесте. Тең қабырғалы үшбұрыш симметриясы тобының көбейту кесте

C3v	E	L3	L32	P1	P2	P3
E	E	P3	L32	P1	P2	P3
P3	P3	P32	E	P3	P1	P2
L32	L32	E	L3	P2	P3	P1
P1	P1	P2	P3	E	P3	L32
P2	P2	P3	P1	L32	E	L3
P3	P3	P1	P2	L3	L32	E

Түрлену тобындағы екі элементтің көбейтіндісі коммутативті емес, яғни жалпы жағдайда A·B≠B·A болатындығы жоғарыда айтылған. Көбейтіндінің осы қасиеттерiн C_3v тобының элементтерiнде көрсетуге болады, мысалы: L₃·P₁= P₂, P₁·L₃= P₃

Осы екі топ элементтері коммутация жасамайтындығы көрініп тұр.

Топшалар – өзі топты құрайтын, топтың көптеген элементтерінің жиынтығы. C_3v тобының төмендегідей топшалары бар:

E, L₃, L₃² – (3); E, P₁ – (2); E, P₂ – (2); E, P₃ – (2); E – (1)

Топшалардың реті – оның элементтерінің саны (жақшадаға сандарға қара). Топшалардың реті топтағы элементтер санының бөлгіші болып келетінін көрсетуге болады. C_3v тобында 6 элемент бар, сәйкесінше олардың топшаларында 1, 2 және 3 реттер бар болып келеді. Математикалық көзқарас тұрғысынан топ толықтай көбейту кестесімен анықталады.

Екі топ егер олардың элементтері арасында өзара сәйкестік болса G және G' изоморфты деп аталады, онымен қоса кез-келген , онда болады, мұндағы A↔A', B↔B' және олар үшін AB↔A'B' (↔символы сәйкестікті білдіреді). Басқаша айтқанда, дәл осы әдіспен, осы топтардың бірінің элементтерінің атауын қайта өзгертсе топтар изоморфты болады. Олардың көбейту кестесі екінші топтың көбейту кестесімен сәйкестікте болуы керек.

Куб тобы.

Куб өсінің O тобы 24 элементтен тұрады және симметрияның түрлі өстерін айнала бұрылатын түрленулерінен тұрады: E; 3L₄; 3L₄²; 3L₄³; 4L₃; 4L₃²; 6L₂ (1.9 -сурет).

1.9-сурет. Куб симметриясының өсі, куб симметриясының жазықтары

Онымен қоса кубтың симметрия жазықтығы мен инверсия центрі i болады. Егер инверсия i операциясын 24 бұрылыспен бірге өткізсек, онда онымен қоса 24 түрлену пайда болады. Нәтижесінде кубтың барлық тобын жоятын 48 элемент түзіледі. Осы 48 элементтен тұратын топ O_h тобы деп аталады. O_h симметриясы сілітілі-галойдты кристалдарының: кремний мен германий (төмендегіге қара) класын анықтайды.

Тетраэдр топтары.

Тетраэдр топтары куб тобының топшалары болып табылады, яғни тетраэдр симметриясының түрленулері куб симметриясының түрленуінің жиынтығы болып саналады. GaAs, InSb кристалдарының симметриясы тетраэдр болып келеді. 1.10-суретте кубтың ішіндегі тетраэдр көрсетілген. Тетраэдрдің инверсия центрі жоқ екені көрініп тұр.

1.10 сурет. Тетраэдр симметриясының өсі және симметрия жазықтығы

Тетраэдр тобына мына түрленулер: E, 3L₄², 4L₃, 4L₃² (12 қарапайым бұрылыс), 6 айналы бұрылыс: 3L_4i, 3L_4i² және 6 жазықтықтағы шағылысу: 6P (симметрия жазықтығы тетраэдр қабырғасы арқылы өтеді) жатады. Тетраэдр тобы T_d арқылы белгіленіп, құрамына 24 түрлену кіреді.