6. Бөлім. Қатты денелердің электрлік қасиеттері

6.1. Қатты денелердегі электрондық күйлер

Қатты денедегі электрондардың энергетикалық спектрін Шредингер теңдеуі көмегімен қарастыруға болады ( – толқындық функция, E – өздік мәні). Бірақ кристалл бір-бірімен өзара байланыста болатын және өте күрделі үздіксіз қозғалыста болатын үлкен жеңіл (электрондар) және ауыр (ядролар) бөлшектерден ( 1 cm³ қа‑ 10²³-10²⁴ бөлшек) тұрады.

Сондықтан  толқындық функциясы барлық электрондар мен ядролардың координатасына тәуелді , мұндағы электрондар координатасын анықтайды,  ядролардың координатасы. Шредингер теңдеуінен кристалл туралы барлық ақпараттарды алуға болады, соның ішінде оның E₁, E₂,.... энергияларының мүмкін болатын мәндерін, сондай-ақ осы энергетикалық күйлерге сәйкес келетін ядролардың конфигурациясы мен электрондардың кеңістікте таралулары. Соңғы ақпаратты толқындық функциясы береді. ² бізге сәйкес электрондар мен ядролардың мәндері туралы ақпарат береді. Егер ²-ты барлық электрондық координаталар бойынша интегралдасақ, онда ядроның күйі үшін энергияның берілген мәнінде барлық мүмкін болатын таралу мүмкіндіктерін табамыз. Осылайша кристалдық тордың кеңістіктік құрылымы анықталуы мүмкін,  ол P максимум мәніне ие болатын, ядролардың конфигурациясына сәйкес келеді. Ядролардың үлкен массаларының нәтижесінде P(R_) олардың координатасына функциясы болып табылады, ол тепе-теңдік күйінің айналасындағы тордың аз жылулық тербелістерінен басқа барлық ядролардың ығысуы кезінде нөлге тең. Егер ға R_ ядролар координатының анықталған Р мәндерін қоя отырып біз, ядролардың тепе-теңдік конфигурациясы кезіндегі тордағы электрон зарядының таралуын табамыз. Есептің шығарылу жолы теориялық қиын, бірақ шын мәнінде шешімді тек көпэлектронды (көптеген бөлшектердің координатаға тәуелділігі) есептің бірэлектрондыға (яғни, берілген ішкі өрісте қозғалатын электрон туралы есеп) мәліметі көмегімен анықтауға болады. Бұл жол кристалдың зоналық энергетикалық диаграммасына жол ашады.

Гамилтон операторы қандай энергия түрлерін қарастыратынын байқайық:

1) электрондардың кинетикалық энергиясы 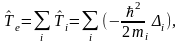мұндағы

m‑ электрон массасы және  i-ші электрон үшін Лаплас операторы;

2) ядроның кинетикалық энергиясы

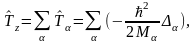
мұндағы M_ ‑ ядро массасы және _  - ядросы үшін Лаплас операторы;

3) қос электрондардың өзара әсерлесуінің энергиясы ;

4) қос ядролардың өзара әсерлесуінің энергиясы ;

5) қос электрондардың ядромен өзара әсерлесуімен энергиясы ;

6) ішкі өрістегі барлық бөлшектердің энергиясы .

Сонымен, бұл ішкі өрістегі кристалл гамилтонианы

(6.1)

(6.1) теңдеуі 3(Z+1)N айнымалыларынан тұрады, мұндағы N – кристалдағы атомдар саны және Z – атомдағы электрондар саны. Жалпы жағдайда теңдеуді шеше алмаймыз. Бір-бірімен әсерлеспейтін бөлшектер жүйесіне көшеміз, сонда бөлшектер жүйесі үшін теңдеу әрқайсысы бір бөлшек қозғалысын сипаттайтын теңдеулер жүйесіне бөлінеді. Шын мәнінде, егер жүйе гамилтонианын былай десек:

‑ тек k- сыншы бөлшектің координатасына тәуелді,

бұл бөлшектер өзара әсерлеспейтіндігін көрсетеді. Енді жүйенің толқындық функциясы жекелеген бөлшектердің туынды толқындық функциясын көрсетеді, ал жүйе энергиясы бөлшектер энергиясының қосындысына тең:

, сондай-ақ . (6.2)

Біздің мақсатымыз әсерлесуші бөлшектер жүйесінен (6.1) әсерлеспейтін бөлшектер жүйесіне (6.2) өту типі болып табылады. Ол тек белгілі жеңілдетулер жағдайындағы келтірілген шешімдер нәтижесінде ғана мүмкін. Бұл жеңілдетулер мыналар:

1. Ішкі өріс жоқ кезінде .

2. Атом ядролары мен электрондары массаларының үлкен айырмашылығы (M_ >> m) олардың қозғалысының үлкен айырмашылығына алып келеді. Сондықтан электрондардың жылдам қозғалысын сипаттаған кезде ядролардың баяу қозғалысын есепке алмай, қозғалыссыз ядролар өрісіндегі электрондар қозғалысын қарастыруға болады. Ядролардың баяу қозғалысын электрондардың баяу орналасуымен туындайтын өрісте емес, ал электрон зарядының орташа кеңістіктік таралуымен туындайтын өрісте қарастыруға болады. Ядроның айтарлық ығысқан уақыты аралығында электрон кристалдағы өз орбитасының барлық нүктелерін бірнеше рет айналып өтіп үлгереді. Мұндай келтіру адиабаталық немесе Борн-Оппенгеймер келтіруі деп аталады.

Ядроның анағұрлым қатаң келтірілуі болады. , болғанда координаталар басын таңдай отырып етуге болады. Енді электрондардың гамильтонианы деп атауға болады және Шредингер теңдеуі болады, мұндағы Е_е – тыныштықтағы ядролардың өрісінде қозғалатын электрондар энергиясы. Ядролардың қозғалысын ядролардың толқындық функциясын ендіру жолымен анықтауға болады, сондай-ақ

,

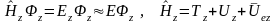мұндағы  кристалдың толық энергиясы, ол үлкен дәлдікпен гамильтонианның ядролық бөлігінің өзіндік мәнімен сәйкес келеді, ал  ядроның электрон зарядының кеңістіктік таралуының өзара әсерлесуінің орташа мәніне сәйкес келеді. Сонымен, адиабаталық келтіруде толқындық функцияны 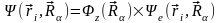туындысы ретінде қарастыруға болады, _е және _z мына теңдіктен табылады.

(6.3)

Сонымен, адиабаталық келтіруде электрондардың қозғалысы ядролардың мезеттік өрісімен анықталады және сондықтан (9.3) өрнекте электрондардың потенциалдық энергиясы мен толқындық функциясы _е ядролардың конфигурациясына тәуелді болады. Ядролардың потенциалдық энергиясы электрон зарядының орташа кеңістіктік таралуымен анықталады. Адиабаталық келтіруде ядролар мен электрондардың нақты орналасу ықтималдығы . Адиабаталық келтірудің дәлдігі энергияда m/M пропорционал, яғни 1/2000 артық. Тордың жылулық қозғалысы және онымен байланысты ядроның аз ығысулары электрондардың энергетикалық спектрлеріне әсер етпейтін, бірақ электрондарды энергияның деңгейлер бойынша белгілі бір таралуын орнататын жағдай ретінде қарастырылады. Бірақ та адиабаталық келтіру есептің негізгі математикалық қиындығын оның көп бөліктілігін жоя алмайды.

3. Келесі келтіру бұл – бірэлектронды келтіру (Хартри-Фок). Мұнда барлық электрондардың мезеттік орналасуына тәуелді әрбір электрондардың басқалармен қосарласып әсерлесуінің энергиясы U_ij, электрон зарядының орташаланған кеңістіктік таралуымен туындайтын электронның өріспен өзара әсері ретінде қарастырылады. Мұндай _i өрістегі i-электронның потенциалдық энергиясы тек қана осы электронның координатасына ғана тәуелді болсын, . Ол басқа қалған электрондардың қозғалысына ғана тәуелді емес, сонымен қатар, берілген электронның қозғалысына да тәуелді (i-электронның қозғалысы өз әсерін барлық қалған электрондарға тигізеді). Сондықтан өріс өзара келісілген деген атауға ие болды. Сонымен, өзара келісілген өрісті енгізу келесі ауысуды жүзеге асыруға көмектеседі

.

Сәйкесінше электрондардың ядромен өзара әсерлесуінің потенциальдық энергиясын барлық ядролардың өрісіндегі i-электронының потенциалдық энергиясы U_i арқылы көрсетуге болады.

.

Өзара келісілген өрісті енгізу кристалдағы электронды өзара әсерлеспейтін бөлшек ретінде қарастыруға мүмкіндік береді, яғни бір біріне тәуелсіз қозғалатын. Осының арқасында, көпэлектронды есеп бірэлектрондыға келеді және (6.2) сәйкес электрондар жүйесінің толқындық функциясы туынды түріне енеді, ал жүйе энергиясы жекелеген электрондар энергиясының қосындысын береді.

Көптеген бөлшектердің есебі бір электрон есебіне жақындайды. Егер кристалдағы электронның потенциалдық энергиясы ядро өрісіндегі электронның және қалған басқа барлық электрондардың потенциалдық энергиясы  ретінде анықталса, , онда Шредингер теңдеуі мынадай болады.

(6.4)

функция түріндегі рационалды таңдаумен байланысты бірэлектронды есеп шешудің бірнеше тәсілдері бар. Көбінесе электрон периодты потенциал өрісінде орналасқан деп болжанады, яғни (6.4) өрнектегі тордың үшөлшемді периодтылығына ие болады.

Бірақ та бұл жолдың көмегімен де қазіргі уақытта электрон қозғалысы үшін өте жеңілдетілген, негізінен үш өлшемді емес бірөлшемді есептерді шешу мүмкін болып отыр. Төменде периодты потенциалдағы бірөлшемді электрон қозғалысына арналған есептің шешу жолы көрсетілген (Кронинг-Пенни моделі).

Екіншіден, екі анағұрлым көп таралған жағдай қарастырылған: 1) күшті байланысты келтіру және 2) еркін электрондарды келтіру.

Күштi байланыстың келтірулері шеңберiнде электронның өз атомының әсерлесуiнiң энергиясы басқа атомдармен өзара әрекеттесуi энергиясынан көбiрек болады. Басқа сөзбен айтқанда, электрондар өз атомдарымен қүшті байланыста болады, олардың энергетикалық деңгейлерiн бірнеше деңгейлерге бөлетін басқа атомдардың электромагниттi өрістері аз әсерін тигізеді. Атомның деңгейлерi сыртқы магниттiк өрiстiң әсерлерінен осылайша бірнеше деңгейлерге ажырайды (Зееман эффектісі ). Атомдардың өзара әрекеттесуi бұл жағдайда оңашаланған атом электронының энергетикалық деңгейлері сипаттамасын айтарлықтай аз өзгертеді.

Кронинг-Пенни моделі. Кронинг-Пенни моделінде электронның қарапайым пішінді периодты потенциалындағы электронның бірөлшемді қозғалысы қарастырылады: ені L бірөлшемді потенциалдық шұңқырда бір бірінен бірдей a қашықтықта әрқайсысының биіктігі V, ал ені b болатын төртбұрышты потенциалдық тосқауылдар орналасқан (6.1-сурет). потенциалдық тосқауылдардың иондық түйіндердің нақты потенциалдарына аса ұқсамайтын мұндай пішіні 6.1-суретте сызбанұсқалық түрде тұтас жұқа сызықтармен бейнеленген. Бірақ та, тіптен мұндай дөрекі модель кристалда қозғалған электрондардың энергетикалық спектрінің негізгі заңдылықтарын көрсете алады.

6.1-сурет - Кронинг-Пенни (а) моделіне сүйеніп жалған потенциалдық энергия түрі және энергия шкаласы бойынша E энергиясының рұхсат етілген мәндерінің таралуы (б).

Мұндай потенциалдық шұңқырдағы электрон үшін Шредингер теңдеуі жуық әдістермен шешілуі мүмкін. Нәтижесінде электронның E энергиясы барлық мәндерді қабылдамауы мүмкін екендігі шығады, нақтырақ E шкаласында энергияның рұхсат етілген мәндері бар бөліктер және энергияның тыйым салынған мәндері бар бөліктері болады (6.1-суретті қара). E шкаласындағы E-нің рұхсат етілген мәндері жоқ аралықты тыйым салынған энергетикалық аймақ (немесе тыйым салынған энергетикалық жолақ) деп аталады, ал E-нің рұхсат етілген мәндері бар аралық рұхсат етілген энергетикалық аймақ (немесе рұхсат етілген энергетикалық жолақ) деп аталады.

Егер тосқауылдар олар арқылы электронның туннелденуін ескермеуге болатындай биік және кең болса, онда электронның қозғалысы туралы есеп электронның бірөлшемді ені a-b потенциалдық шұңқырдағы қозғалысына ұқсас. Электрон осы кішкентай потенциалдық шұңқырда локалданған болады («өзінің» атомындағыдай). E шкаласындағы электрон энергиясының мәндерінің таралуы 6.2(б)-суретте көрсетілген; рұхсат етілген мәндері бір-бірінен оқшауланған.

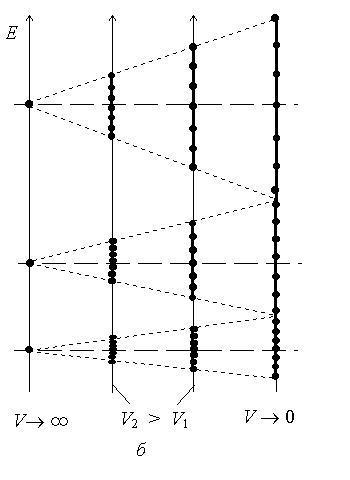
6.2-cурет - Крониг-Пенни моделіне сүйеніп жасалған потенциалдық энергия түрі (а), және E энергия шкаласы бойынша энергияның рұхсат етілген мәндерінің таралуы (б).

Биіктіктер мен ендерінің аралық мәндерінде сурет E мәндерін жуықталған әдістермен есептейді. Мұндай жағдайларда рұхсат етілген мәндер суретте көрсетілген. Осы суретте тосқауылдардың биіктігі артқанда рұхсат етілген және тыйым салынған энергетикалық аймақтардың шекараларының орны өзгеретіндігі көрсетілген, нақтырақ, тыйым салынған аймақтардың рұхсат етілгендер есебінен кеңейеді. Потенциалдық тосқауылдардың толық өтімді болмауы шегінде рұхсат етілген аймақта бір деңгейге дейін тарылады. Мұндай жағдай оқшауланған атомдарға тән, бұл жағдайда электрон өзінің атомының маңында локалданады; күшті байланыстың жуықтауына сәйкес келеді.

Күшті байланыстың жуықтауы. Бұл жуықтау қарастырылған атомдағы электронның байланыс энергиясы осы электронның басқа атомдар жасайтын өрістерімен әсерлесу энергиясынан үлкен деп болжауға негізделеді. Мұндай жағдайда конденсирленген күйде (кристалда және сұйықта) оқшауланған атомдардың электрондық күйлерімен ұқсас болуы керек, себебі атомдардың бір-бірімен әсерлесуі атомның электрондық күйінің жүйесін түбірімен өзгерте алады. Күшті байланыстың жуықталуы өздерінің атомдар жағдайын, мысалы, иондық және ковалентті кристалдар жағдайындағыдай электрондардың энергетикалық деңгейлері жүйесін жақсы сипаттайды. Деңгей жүйелерінің жуық түрі атомдар бір-бірімен өздері жасайтын электрлік және магнит өрістерімен әсер етеді және бұл өрістер атомның жекелеген туындаған (вырожденный) деңгейін бірнеше ішкі деңгейлерге жіктелуге әкелетіндігін еске алып алдын-ала айтуға болады. Мұндай жағдайда конденсирленген затта оқшауланған атомдардың жекелеген деңгейлерінің орнында энергияныңқандай да бір диапазонында деңгейлердің үлкен жиынтығы алынуы керек. Мұндай жиынтықты рұхсат етілген энергетикалық аймақ деп атау келісілген.

Алдымен бір-бірінен алыс орналасқан N атомды қарастырайық. Сонда атомдардың әсерлесуін ескермеуге және олардың әрқайсысы бірдей болатын деңгейлердің энергиясының белгілі бір мәндеріне ие болады деп санауға болады. N атомды жүйенің барлық деңгейлері 2N еселі туындаған болады (2 спинді ескергендіктен пайда болады). Атомдар жақындаған кезде деңгейлер энергиясының азаюы атомдардың бір-біріне өзара тартылуы нәтижесінде атомдардың энергиясының азаюы есебінен болады. Бұдан басқа, деңгейлер олар түзетін өрістер атомға жақындаған сайын артатындықтан атомдар неғұрлым жақын орналасқан сайын соғұрлым олар күштірек ыдырайды. Атомдар арасы кристалл торының периодындай болғанда бұдан ары жақын келген атомдар тебіліп, ал олардың әсерлесу энергиясы күшті артатындықтан деңгейлердің энергиясының максимумы бақылануы керек. Мұндай жағдайда атомдар деңгейлерінің энергиясының олардың ара қашықтығына тәуелділігі 6.3-суретте көрсетілгендей болады. Шындығында қатты ыдырауға сыртқы валенттік электрондарға сәйкес келетін деңгейлер ұшырайды.

6.3-сурет - Атомдар деңгейлерінің энергияларының олардың d ара қашықтығына тәуелділігі

6.3-суретте туындамаған деңгейге жауап беретін және N атомдарға тән, кристалды оқшаулайтын және кристалды құрайтын электрон күйінің жалпы саны сақталатындығы, сондай-ақ 2N -ге тең болатындығы көрінеді.

Оқшауланған атомның бір деңгейіне жауап беретін күйлер саны екіге емес, осы деңгей туындаған жағдайда үлкен санға тең болуы мүмкін. Сонда күйлердің жалпы саны оқшауланған атомның туындауының еселігіне көбейтілген 2N -ге тең болады.

Атомдардың арасындағы әсерлесу елеулі болған жағдайда, бұл жекелеген аймақтың жабылуына әкелуі мүмкін, мұндай жағдайда жабылатын аймақтардағы күйлердің қосындысы электрондық күй санына тең бір аймақ пайда болады. Осы жағдайда электрондық күйлер 2N -ге еселі болады.

Дерліктей еркін электрондар моделі. Мысалы, металдық атомдардағыдай сыртқы электрондары «бірігетін» және салыстырмалы түрде кристалда еркін орын ауыстыратын, кристалдық заттың үлкен тобы бар. Бұл жағдайда еркін электрондардың кристалда электрндар өлшемі кішігірім қозу деп санауға болатындай периодты орналасқан иондық түйіндердің әлсіз өрісіндегі кристалды потенциалдық шұңқырдың ішінде қозғалады деп санайтын дерліктей еркін электрондар моделі өте сәтті болады.

Бірінші жуықтау ретінде электрондар жағдайын сипаттау үшін кристалдағы иондық остовтардың өрісін ескермейді және электрондардың Ферми-газ моделін қолданады, қысқаша әрі еркін электрондар жуықталуы деп аталатын осы теорияның негізгі тұжырымдарын қарастырамыз.

Электрондардың толқындық векторларының кеңістігінде электрондық күй жүйелер жүйесін қыры L болатын куб пішіндес үшөлшемді потенциалдық жәшік үшін Шредингер теңдеуін шешу нәтижесінде алады. Периодты шекаралық шарттар жағдайында ψ толқындық функциясы үшін электрондар күйі толқындық векторлар мәнінің рұхсат ететін мәндері болады:

(6.5)

мұндағы 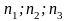- бүтін сандар, себебі шамаларының өзгеру қадамы L шамасы үлкен болатындықтан ұсақ болады, онда -ге тәуелді функциясы үздіксіз функциясы ретінде қарастырылады. Электрондардың толқындық функциялары мына түрде болады:

(6.6)

Мұндағы . Электрондардың кинетикалық энергиялары (олардың потенциалдық энергиясы нөлге тең) келесі формуламен есептеледі:

(6.7)

T=0К температурада барлық N электрондар Паули принципін сақтай отырып E-нің ең аз мәндерімен күйге ие болуға тырысады. Бұл жағдайда k кеңістікте бос емес күйлер k_F радиусты шар пішіндес болады. бұл шардың беті Ферми беті, ал оған жауап беретін энергия Ферми энергиясы деп аталады. Ферми энергиясы n еркін электрондар концентрациясына тәуелді және келесі формуламен есептеледі:

(6.8)

Температура артқанда күйлерге электрондардың орналасуы келесідей күйлердің бос болмау функциясымен беріледі:

(6.9)

Функцияның әр түрлі температурадағы графигі 6.4-суретте көрсетілген

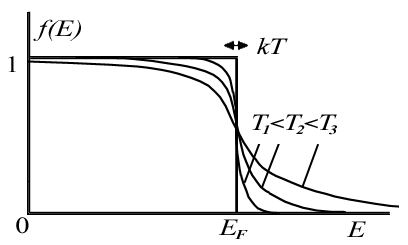
6.4-сурет - Әр түрлі температурада Ферми-газ электрондарының күйлерді толтыру функциясы

Барлық металдар үшін барлық температурада олардың балқу температурасын қоса алғанда Ферми энергиясы шамадан 50-200 есе артық болады. Сондықтан металдарда электрондық газ күшті туындаған электрондардың Ферми-газ сияқты қарастырылады. Температура артқанда Ферми энергиясы елеусіз артады және келесі формуламен беріледі:

(6.10)

Осылайша, температураның артуы кеңістікте Ферми бетінің елеусіз жайылуына (размытию) әкеледі.

Дерліктей еркін электрондар моделінде иондық түйіндердің потенциалы кристал торының параметрлеріне сәйкес периоды периодтық функция ретінде қарастырылады:

       (6.11)

Иондық остовтардың потенциалдары тек ядро зарядының иондық остов электрондарымен экрандалу (қалқалану) эффектісінен иондық орталыққа жақын аз облыста ғана үлкен шамаға ие болады. Сондықтан иондық остовтардың потенциалы кішігірім қозу ретінде қарастырылады.

(6.10) түрдегі потенциалдық энергиялы периодты өріс пайда болғанда (6.11) толқындық функциясы келесі формулаға сәйкес өзгереді деген Блох теоремасы бар:

       (6.12)

мұндағы 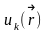- және -ға тәуелді және иондық түйіндердің потенциалдық энергиясы секілді периодқа ие периодты функция. Дерліктей еркін электрондарда жуықтап, кристалдың ішіндегі барлық кеңістікте бірге жуық, және иондық остовтардың «ішкі» кіші облыстарында ғана олар айтарлықтай бірден ерекшеленеді.

     Дерліктей еркін электрондар моделінде ионды остовтардың периодты өрісін ескеру электрон энергиясының толқындық векторға, жеке алғанда оның кристалдағы бағытына тәуелді өзгеруіне әкеледі. Осының салдарынан Ферми беті сфералық болмайды және неғұрлым күрделі пішінге ие болады, дегенмен ол кристалда электрон энергиясының -ға тәуелділігі үшін қатынасы орындалатындықтан ол центрлік симметриялы болады.

функциясының елеулі ерекшеліктері Бриллюэн аймағының шекарасының маңында байқалады (1.3 бөлімді қараймыз). Көрнекілік үшін a периодты қарапайым куб кристалл торын қарастырамыз. Электрон [100] бағытымен қозғалсын және толқындық векторға ие болсын делік. Егер біз ионды остовтардың өрістерін ескермесек, онда 6.7- суреттегідей толқындық векторға энергияның квадраттық тәуелділігін алар едік.

Білетініміздей электрон толқындық қасиетке ие, жеке алғанда ға тең де-Бройл толқынының ұзындығына ие. немесе дәл сол сияқты болғанда осіне қарсы бағыттағы иондардан шашыраған толқындардың күшею шарты орындалады, шындығында көршілес атомдармен шашыраған толқындардың оптикалық жол айырымы 2a тең, да электронның бүтін де-Бройл толқын ұзындығы дәл сияды. Сонда түскен толқынмен интерференцияланатын интенсивті шағылған толқын пайда болады, бұл тұрғын толқынның түзілуіне әкеледі.

Тұрғын толқын кубтық тордың «түйіндерінде» шашақтануы немесе олардың арақашықтығының «ортасында» шоқтануы мүмкін (6.5-сурет). Шашақтар басқа нүктелерде орналаса алмайды, себебі, мұндай жағдайда кристалл торына қатысты электрондық бұлттың шашақтануының орналасуының симметриялылығы бұзылар еді.

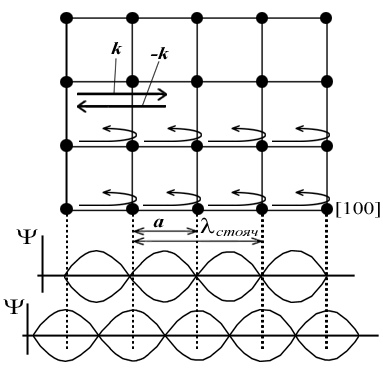
6.5-сурет - Периодты a кубтық кристалл торындағы электронды толқындардың таралуының сызбанұсқасы және осы торда (а) тұрғын толқынның пайда болуы; электрон энергиясының еркін электрондар моделінде және дерліктей еркін электрондар моделінде толқындық векторға тәуелділігі (б)

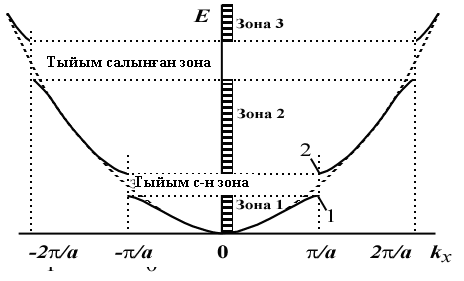
6.6-сурет - a периодты кубтық кристалл торда электрондық толқындардың таралу схемасы және осы торда тұрғын толқынның түзілуі. Электрон энергиясының еркін электрондар және дерліктей еркін электрондар моделінде оның толқындық векторға тәуелділігі

Tолқындық функцияның модулінің квадраты мен электронның бар болу ықтималдығының тығыздығы және кристалдағы орташа электрондық тығыздық байланысты. Шынымен де тұрғын толқынның шашақтарының (толқындық функцияның және электрондық тығыздықтың максимумдарының) кристалл торының иондарының орнында орналасқанда оң зарядталған иондармен электрондық бұлттың (теріс зарядталған) әсерлесуінің кулондық энергиясы тұрғын толқынның шашақтары кристалл торының иондарының арасында орналасқандағыдан аз болады. Осылайша, болғанда функциясының мәнінің бір емес айтарлықтай ерекшленетін екі мәні болады. үздіксіз екендігін ескеріп ның қалған барлық мәндерінде 6.6-суреттегідей тәуелділігінің графигін тұрғызуға болады.

Бұл нәтижені [100] параллель емес толқындық векторлы электрондарға жалпылауға болады (6.5-сурет). Сонда векторының соңы Бриллюэн аймағының шекарасына түскенде (1.20) ға сәйкес Вульф-Брегг шарты орындалады және интенсивті шағылған толқын қалыптасады. Осылайша Бриллюэн аймағы шекарасында 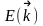тәуелділігінің үзілуі байқалуы керек. Бриллюэн аймағындағы күй саны 2N-ге тең (электрон спинін ескергенде). Ол энергетикалық аймақтағы күй санына тең. Осылайша күшті байланыс моделіне де, дерліктей еркін электрондар моделіне де сәйкес электрондар энергиясы шкаласында рұқсат етілген және рұқсат етілмеген аймақтар деп аталатын энергияның рұқсат етілген және рұқсат етілмеген бөліктері болады, әрбір рұқсат етілген аймақтағы күй саны кристалл атомының екі еселенген санына еселі.

Кристалдық тордағы электрондар динамикасы. Кванттық теорияның маңызды және күтпеген нәтижесі кристалл торының периодты потенциалын ескеру электронның еркін кеңістіктегі қозғалысымен салыстырғанда электрон қозғалысының тұрпатын түбегейлі өзгертпейді.

Кристалда электрондар қозғалысын қарастырғанда келесідей анықталмағандық қатынасын ескеру керек:

(6.13)

Мұндай жағдайда диапазонда ретті мәнге ие қандай да бір жылдамдықпен қозғалып келе жатқан өлшемі ретті кеңістіктің қандай да бір аймағындағы электронның орны туралы айтуға болады. Осы кезде электронның импульсімен байланысқан толқындық векторы қандай да бір анықталмағандыққа ие болуы керек. Еркін электронның толқындық функциясы келесі түрдегі жазық толқын:

(6.14)

болатындықтан мәнге ие электронға қандай да бір диапазонда толқындар теориясына сай толқындық жиынтық (пакет) сәйкес келеді. Толқындық жиынтықтың амплитудасының максимумының таралу жылдамдығы дәлірек топтық жылдамдық былай анықталады:

   (6.15)

Нақ осы жылдамдық толқындық жиынтықтың және онымен байланысқан электронды кездестіру ықтималдығы ең үлкен болатын кеңістіктің облысының орын ауыстыруын сипаттайды. Топтық жылдамдық ұғымы үш өлшемді күй таралуына жалпыланады: үш өлшемді кеңістікте топтық жылдамдық векторы функция градиенті сияқты беріледі. Ол Ферми бетіне перпендикуляр.

Электронның классикалық бөлшек ретінде сыртқы күштің әсерінен қозғалысын қарастырамыз. мәнінің қалай өзгеретіндігін есептейміз. Ол үшін -дің уақыт бойынша туындысын есептейді (классикалық механикадағы үдеуге аналогы). күш векторы топтық жылдамдық үшін бір түзудің бойымен бағытталған. Сонда тің -нің осы өске проекциясы үшін мынаны аламыз:

(6.16)

Бұл формуланы мына түрде қайта жазуға болады:

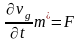(6.17)

(6.18)

Ол келесідей қабылданғанда Ньютонның екі заңына ұқсас:

(6.19)

- шамасын электронның эффективті массасы деп атау келісілген. Оның мәнінде жанама түрде кристалдың периодты өрісінің электронның толқындық векторынан электронның энергиясының өзгеру заңына әсері ескерілген.

Электронның эффективті массасы электронның массасынан елеулі ерекшеленеді және (6.19) -ға сәйкес электронның әртүрлі толқындық векторлары үшін әртүрлі мәнге ие. модулінің аз мәнінде (6.6-суретте) функциясының екінші ретті туындысымен берілетін оның мәні оң болады, ал Бриллюэн аймағы шекарасына жақын мәнінде теріс болады. Соңғы жағдайда күштің ықпалы сыртқы күшті үдетпейді, керісінше электронды тежейді. Мұнда ешқандай парадокс жоқ, себебі, тежелу кристалдың периодты өрісінің электрон қозғалысына ықпал етуіне байланысты. Мұндай электрондар сыртқы электромагниттік өрістерде теріс массалы бөлшектер сияқты немесе оң зарядталған бөлшектер сияқты ұстайды. Мұндай бөлшекті теріс массаға ие немесе қарсы таңбалы зарядты бөлшектер деп санауға болатындығын айта кетеміз, себебі, сыртқы электромагниттік өрістің әсерімен бөлшектің үдеуі өз таңбасын масса таңбасы өзгергенде де, сондай ақ заряд таңбасы өзгергенде де өзгертеді. Мұндай оң зарядталған бөлшектерді кемтіктер деп атау келісілген.

6.6-суретте мұндай иілістерге (6.19)-ға сәйкес шексіз (немесе өте) үлкен эффективті масса сәйкес келеді. Мұндай электрон іс жүзінде сыртқы күштің әсерінен өзінің жылдамдығын өзгертпейді.

Электрондардың басым бөлігі үшін эффективті масса ережеге сай оң. Жеке алғанда, егер аймақтар жартылай толса немесе одан аз болса, (6.6-суретті қара) барлық электрондар оң. Теріс эффективті массаға тек Бриллюэннің бірінші аймағының шекарасының маңындағы күйдегі электрондар ғана ие болады.