3.2. Сызықтық ақаулар

Дислокация деп аталатын кристалды тордың сызықтық ақауларын тереңірек зерттеу, олардың барлық кристалды материалдардың беріктігі мен икемділігіне қатты әсер етуімен байланысты. Осы ақаулардың болуын ескермеген кристаллдардың беріктік теориясы монокристаллды және поликристаллды заттарда байқалған механикалық қасиеттерді түсіндіре алмады.

Дислокацияның типтері. Дислокацияны аймақтық және бұрандалы деп екіге бөлу қалыптасқан, дегенмен байқалатын дислокацияларда әдетте осы екі типтің элементтері бола береді. Қарапайымдылық үшін жәй кубты торды қарастырайық, бірақ алынған нәтижелер шамалы өзгерістермен басқа да типтердің торлары үшін дұрыс.

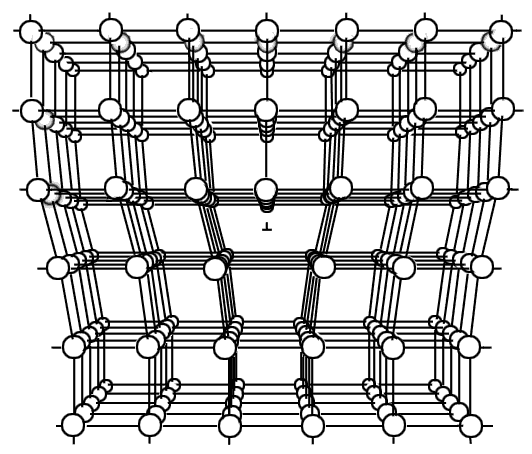
Аймақтық дислокация атомдардың ерекше орналасуымен сипатталады, 3.2-суретте қарапайым кубты тор көрсетілген. Бұл суретте 100 типіндегі екі көрші бүтін жазықтар арасына орналастырған жазықтықтың "артық жартысы" бейнеленген. Бүтін жазықтардың атомдары бір-бірімен байланыстарын қалыптастырды, бірақ енгізілген жарты жазықтықтың шетінде үлкен деформация пайда болды. Артық жарты жазықтықтың шеті арқылы өтетін сызықты аймақтық дислокация сызығы деп атайды, кейде жәй аймақтық дислокация деп те атайды. Сондықтан да дислокацияны сызықтық ақауларға жатқызады. Ол артық жарты жазықтықтың шеті орналасқан, осы жарты жазықтық әсерінен болатын кристалдық тордың күшті майысқан жері арқылы өтеді. Кристалдық тордың дислокациясы маңындағы күшті майысқан облысы 2-3 периодқа созылады. Үлкен арақашықтықта бұрмалану аз болады және оларды серпімділік теориясында қарастыруға болады.

3.2-сурет - Дислокация жанындағы атомдардың орналасуының сұлбасы

Аймақтық дислокация 3.2-суретте көрсетілгендей сызба бойынша кристалдардың деформациясы кезінде жиі кездеседі. Сырғу жазықтықтары деп аталатын, атомдары тығыз орналасқан жазықтықта жылжу деформациясы болған кезде дислокация пайда болады.

{100} типіндегі жазықтығы бар қарапайым кубты тор жағдайын қарастырамыз. КЦК торы үшін сырғу жазықтықтары - {110}, {112}, және {123}, ал ҚЦК торлары үшін - {111} болып табылатынын айтып кетейік. Егер кристаллға күш әсер етсе (3.3-сур.(1) қара), онда (100) жазықтығы пунктирмен белгіленген жерге дейін "жыртылуы" мүмкін (3.3-сур. (2)), одан кейін 1 жазықтығының жоғарғы жартысы төменгі жартыға қосылады 2 (3.3-сурет (3)), ал 2 жазықтығының жоғарғы жартысы "артық" болып қалады. Егер кристалға әсер етуді жалғастырсақ, онда келесі жазықтық бөлініп кетеді де, кейін 2 жазықтығының жоғарғы жартысы 3 жазықтығының төменгі жартысына қосылады (3.3-сурет (4)), және т.с.с. жалғаса береді. Осылайша кристаллда артық жарты жазықтық (100) пайда болады, ол күшінің әсерінен көрші жарты жазықтықтардың қосылу-айырылуы арқасында сырғу жазықтығы бойынша жылжи береді. Жаңа жазықтықтың айырылуы дислокация сызығының бойында жүзеге асады, өйткені онда кристалдық бұрмалану жоғары болады (3.3-сурет.).

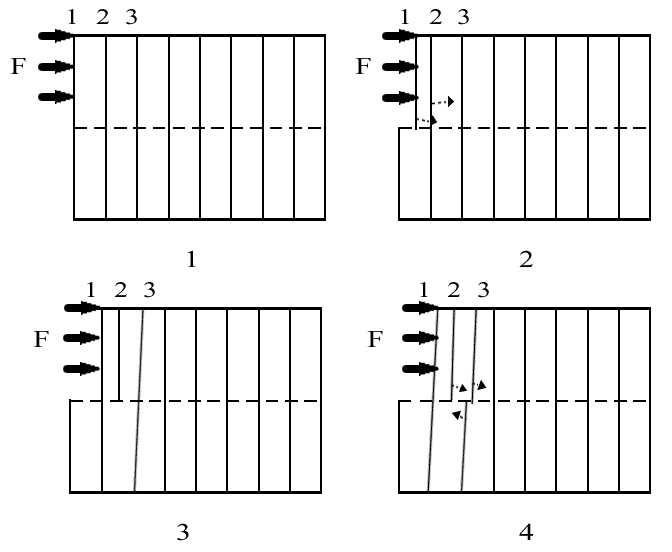
3.3-сурет - Кристалдың жылжымалы деформациясы кезіндегі аймақтық дислокацияның туындауы мен орын ауыстыру сұлбасы

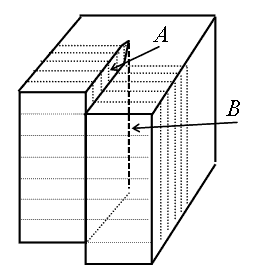
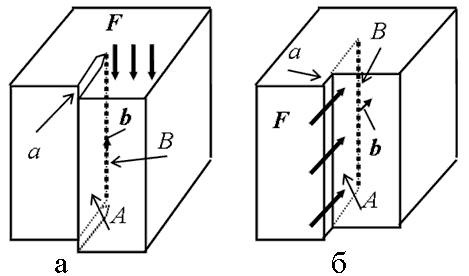
Бұрандалы дислокация. Бұрандалы дислокация 3.4-суретте қарапайым куб үшін көрсетілген, атомдардың ерекше орналасуымен сипатталады. Осы суретте А жарты жазықтығының сол жағында орналасқан атомдар орындарында қалған, ал оның оң жағындағы атомдар бір жазықтық арасы қашықтығына төмен ығысқан. Мұндағы В сызығының жанында үлкен деформация пайда болған. А жарты жазықтығының қыры арқылы өтетін В сызығын және қалған жарты жазықтықты бұрандалы дислокация деп атайды. 3.4-суретте (001) типіндегі горизонталь деформацияланған жазықтықта В сызығы бойынша айналу кезінде кристалдық тордың бір периодына көтерілуге болады, ал В сызығы бойынша бірнеше рет айналған кезде тордың бірнеше периодына көтерілуге болатындығы көрсетілген.

Көтерілу бұрандалы автожол бойынша қозғалысқа ұқсас, осыдан бұрандалы дислокация ұғымы пайда болды. Бұрандалы дислокация жағдайында барлық (010) жазықтықтар өзімен өзі бола алмайды, олар өсі В болатын күрделі бір бұрандалы бетке бірігіп кетеді. 3.4-суретте көрсетілген бет В сызығын айнала сағат тілшесіне қарсы қозғалысы кезінде көтерілісті қамтамасыз етеді (егер жоғарыдан қараса). Мүмкін В сызығын айнала сағат тілшесімен қозғалған кездегі көтерілісті қамтамасыз ететін дәл сондай бет түзген шығар (ол үшін 3.4-суреттегі кристаллдың оң жағын төменге емес жоғары қарай ығыстыру керек еді). Сондықтан бұрандалы дислокация оң бұрандалы және сол бұрандалы болады.

3.4-сурет - Бұрандалы дислокацияға атомдық жазықтардың жақын орналасу сұлбасы

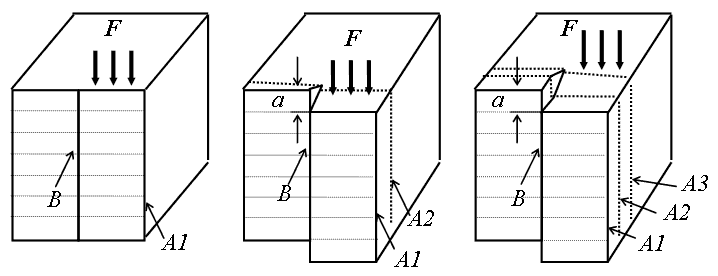
3.4-суретте көрсетілген сызба бойынша бұрандалы дислокация кристалдың деформациясы кезінде пайда болады. {100} типіндегі жазықтықты қарапайым кубты тор жағдайында қарастырамыз. Егер кристалға күшімен әсер етсек (3.5-сурет (а)), онда бағытталған кесіндімен белгіленген орында А1 жазықтығы В сызығы бойынша "айырылады", одан кейін А1 жазықтығының жоғарғы және төменгі жартылары тордың 1 периодына жылжумен қосылады (3.5-сурет (б)). Егер кристалға әсер етуді жалғастырсақ, онда келесі жазықтық айырылады А2 жазықтығының үстіңгі және жоғарғы жартылары жылжумен қосылады (3.5-сурет (в)), және т.с.с. жалғаса береді. Осылайша, кристалда бұрандалы дислокация пайда болады, ол кристалға әсер еткенде жазықтықтардың көрші жартыларының қосылу-айырылуы арқасында сырғу жазықтығы бойынша жылжи береді. Жаңа жазықтықтың айырылуы дислокация сызығының бойында болатынын ескеру керек, өйкені онда кристалдық тордың бұрмалануы көбірек болады (3.5-суретке қара).

а) б) в) 3.5-сурет - Кристалдың жылжымалы деформациясы кезінде бұрандалы дислокацияның туындауы мен орын ауыстыруының сұлбасы

Бюргерс векторы. Бұрандалы дислокацияны кристаллдың келесі модельді операциялар арқылы алуға болады (3.6-суреттегі (а)). Кристаллда (100) жазықтығы бойынша, кристаллды тор түйіндері арасынан өтетін, А жарты жазықтығынан ойша қиық жасайық. Сосын оның оң жағындағы атомдарды төмен қарай бір жазықтық аралық қашықтыққа жылжытып, атомдарды қайтадан А арқылы өтетін байланыспен байланыстырайық. Кристалдың оң жағындағы векторға қатысты сол жағындағы ығысу векторы В бұрандалы дислокациясының Бюргерс векторы деп аталады. Бұрандалы дислокациясының Бюргерс векторы осы дислокацияға параллель болатындығы көрініп тұр.

3.6-сурет - Аймақтық және бұрандалы дислокация кезіндегі кристалдағы атомдардың ығысу сұлбасы. - Бюргерс векторы

Дәл осындай әдіс арқылы аймақтық дислокацияны да алуға болады (басқа сырғу жазықтығына жауап беретін). Ол үшін кристалдың «оң» жағын А жазықтығы бойынша «бізден ары қарай» ығыстыру керек және В дислокациясы сызығының бойында орналасқан атомдардан басқа барлық атомдар арасындағы байланыстарды жетілдіру керек (3.3-суреттегі (а)). Кристалдың осы бөлігіндегі ығысу векторы аймақтық дислокацияның Бюргерс векторы болады. Аймақтық дислокацияның Бюргерс векторы дислокацияға перпендикуляр болатындығы көрініп тұр.

Дислокация тығыздығы. Дислокацияны бақылау әдісі. Кристалдарда дислокация тығыздығы кристалл ішінде таңдалған, бірлік бетті қиып өтетін дислокация санымен сипатталады, немесе, басқаша айтқанда, кристаллдың бірлік көлеміндегі дислокация ұзындығының сомасымен сипатталады. Дислокация тығыздығының мәні және осы дислокация тығыздығына қолданылатын олардың бақылау әдістері төмендегі 7-кестеде көрсетілген

7-кесте. Дислокация тығыздығының мәні және оларды бақылау әдістері

Дислокацияны зерттеу әдістері	Үлгінің қалыңдығы, мкм	Дислокация бейнесінің ені, мкм	Дислокацияның 1см2 дегі максималді тығыздығы
Электрондық микроскопия	10-0-10-1	10-2	1011-1012
Рентгендік топография (өтімділік үшін)	102-103	5	104-105
Рентгендік топография (шағылысу үшін)	2-50	2	106-107
Оптикалық микроскопия (өңдеу шұңқырлары бойынша)	Кез-келген	0,3-0,5	10-6-10-7

Кез-келген тығыздықтағы дислокацияны электронды микроскоп арқылы, ал жақсы жетілдірілген, идеал монокристалдардағы дислокацияларды рентгендік топография (идеал, жетілдірілген кристалл арқылы өткен рентгендік сәуленің интенсивтілігін өлшеуге немесе суретке түсіруге негізделген әдіс) арқылы байқауға болады. Дислокацияны бақылау әдістері дислокацияның өзін емес, кристалдық тордың бұрмалануын көрсететіндігін айту керек.

Кейде дислокацияның іздерін арнайы таңдалып алынған химиялық өңдеу арқылы кристалдың бетіндегі «өңдеу шұңқырлары» бойынша байқауға болады. Бұл әдіс мынаған негізделген, өңдеуші кристалдық тордың дислокациясы маңындағы бұрмалау жақтарын қатты ерітеді, сондықтан дислокацияның кристалл бетіне шығатын орындарында шұңқырлар көрінеді. Жарық микроскобын пайдалану барысында оның рұқсат ету шегі 0,5-1 мкм–ге дейін болатындығын ескеру керек, яғни дәл осындай арақашықтықта орналасқан "өңдеу шұңқырлары" бөлек-бөлек болып көрінеді, ал дислокацияның тығыздығы жоғары болғанда бірігіп кетеді.