ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

Л.Н.Гумилев атындағы Еуразия ұлттық университеті

Даулетбекова А.К., Ақылбеков Ә.Т.

КОНДЕНСИРЛЕНГЕН КҮЙ ФИЗИКАСЫ

Астана – 2014 ж.

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

Л.Н.Гумилев атындағы Еуразия ұлттық университеті

Даулетбекова А.К., Ақылбеков Ә.Т.

КОНДЕНСИРЛЕНГЕН КҮЙ ФИЗИКАСЫ

Оқулық

Астана - 2014 ж.

УДК 538.9(075.8)

ББК 22.37я73

К 55

Физика-математика ғылымдарының

докторы, профессор: А.Т. Ақылбеков

Физика-математика ғылымдарының

кандидаты, доцент: А.К. Даулетбекова

Пікір берушілер:

Физика-математика ғылымдарының

кандидаты, профессор м.а.: А.К.Морзабаев

РhD доктор, доцент: М.М.Муратбеков

К55 Л.Н. Гумилев атындағы Еуразия ұлттық университетінің Ғылыми кеңесінің шешімімен ба

спаға ұсынылған № хаттама 2014

Даулетбекова А.Қ., Ақылбеков Ә.Т «Конденсирленген күй физикасы» пәні бойынша оқу құралы. - Астана. Л.Н.Гумилев атындағы ЕҰУ, 2014.- 175 бет

ISBN

«Конденсирленген күй физикасы» оқулығы «Физика», «Ядролық физика» және «Техникалық физика» мамандықтарының мемлекеттік білім стандартына, типтік және жұмыс оқу бағдарламасына сәйкес жасалған. «Конденсирленген күй физикасы» пәнінің мазмұнын толық қамтиды. Оқулықта идеал кристалдардың геометриясы, топтар теориясы, байланыс түрлеріне байланысты кристалдардың классификациясы, кристалдардағы ақаулар және қатты денелердің механикалық, жылулық, электрлік, оптикалық қасиеттері қарастырылады.

УДК 538.9(075.8)

ББК 22.37я73

© Л.Н.Гумилев атындағы Еуразия

ұлттық университеті, 2014

КІРІСПЕ

Атомдық-молекулалық деңгейде зат газ, сұйық және қатты дене күйінде бола алады. Конденсирленген күй физикасы: 1) конденсирленген фазаның атомдары немесе молекулалары бір біріне жақын орналасады және күшті әсерлеседі және 2) осы конденсирленген фаза қоршаған ортадан «конденсирленген материя-вакуум» беттері арқылы нақты ажыратылған болады. Осылайша, конденсирленген күй физикасы заттың газ күйін қарастырмайды.

Конденсирленген зат атомдары мен молекулалар екі түрлі:

• тербелмелі – атомдар мен молекулалар қандай да бір тепе-теңдік күйінің төңірегінде тербеледі, осы тербелістің амплитудасы, атомдар немесе молекулалар арасындағы қашықтықпен (d) салыстырғанда аз болады;

• трансляциялық – нақты жағдайда жеке атомдар мен молекулалар жүйенің ішінде олардың өзара ара қашықтығымен (d) салыстырғанда үлкен қашықтыққа дейін орын ауыстыра алатын қозғалысқа қатысады.

Тербелмелі қозғалыстың сипаттамалық уақыты ~10^-13 -10^-12с, ал қатты дене бойынша бөлшектің көшу процесіне тән сипаттамалық уақыт 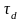~10³ -10⁴с (яғни сағат бойы барлығы қозғалыссыз болады). Уақыт шкаласында және бір-бірінен қатты ерекшеленеді. Тек қатты денені қандай да бір 1000-3000К температураға дейін қыздырған кезде, яғни қатты дене балқығанда секунд үлестерімен өлшенеді, бірақ бәрібір және бір-бірінен миллион есе ерекшелінеді және уақыт бойынша процестер шатастырылмайды.

Заттың екі агрегаттық күйі – сұйық және қатты дене (олар конденсирленген күйлер деп аталады) – күшті әсерлесетін бөлшектерден тұрады. Осындай денелердегі атомаралық қашықтық тартылыс және тебіліс күштері теңесетіндей болып орнайды. Сондықтан конденсирленген заттар өз көлемінің өзгеруіне үлкен кедергі жасайды. Осылардың ішінде мұнымен қоса өз пішінінің өзгерісіне үлкен кедергі жасайтындары қатты денелер деп аталады. Қатты дене мен сұйықтың арасындағы шекара қатаң түрде анықталмаған. Сұйыққа қатты денелер (көлемін сақтайды, бет түзеді, айырылып кетуге қарсы қандай да бір мықтылығы бар) мен газдардың (ыдыс көлемін ала алатын) кейбір қасиеттері тән, алайда тек сұйықтардың өзіне тән қасиеттері де бар, олардың ішіндегі маңыздысы – аққыштық.

Көп жылдар бойы конденсирленген күй физикасының нысандары ретінде бөлшектері жоғары тәртіппен орналасқан құрылымы бар кристалдық қатты денелер алынды. Идеал кристалдар - атомдары немесе иондары қатаң тәртіппен орналасқан үш өлшемді жүйе болып табылады. Әрине, кристалды құрайтын бөлшектердің ретпен орналасу әдісі сан түрлі. Үш кеңістікті өстер (а₁, а₂, а₃) бойынша қайталанатын атомдар арасындағы қашықтықтардың бірдей немесе әр түрлі болуына, сонымен қоса периодты атомдар тізбегінің арасындағы бұрыштарға (α, β, γ) байланысты кристалдар симметриясы және беттік шектері бойынша ерекшеленеді.

Бұл курста біз қарапайым кубты симметриялы кристалдардың бірнеше кластарын: 1) сыртқы электрондық қабықшалары толықтай толтырылған атомдардан –Ne, Ar, Kr, Xe құралған молекулалық кристалдарды және 2) сыртқы электрондық қабықшалары толтырылған оң иондар (катиондар) мен теріс иондардан (аниондар) құрылған ионды кристалдарды қарастырамыз. Мысалы, KCl≡K⁺ Cl⁻, MgO≡Mg²⁺O²⁻, CaF₂≡Ca²⁺(F⁻F⁻).

Идеал молекулалық және ионды кристалдардың құрылымдары қарапайым және өте жақсы зерттелген. Осындай жүйелерде біз идеал құрылымның негізгі ауытқуларын нүктелік, сызықтық және беттік ақаулар деп аталатын- идеал периодты құрылымнан ауытқуларды қарастырамыз. Идеал және нақты (ақауларымен) қарапайым моноатомды немесе бинарлық кристалдардың құрылымы қарапайым және көрнекті, сондықтан осындай кристалдарды зерттеу ұзақ уақыт бойы қатты дене физикасының негізгі мәселесі болып табылған. Техниканың дамуы үш немесе одан да көп элементтерден тұратын күрделі кристалдық жүйелерді зерттеуді талап етті. Мысалы, СаSiO₄ қарапайым катиондардан – Са²⁺ ионынан және молекулалық құрылымы бар аниондардан – (SiO₄)^2- тұрады: кішкентай ион Si (кремний) төбелерінде оттегі орналасқан тетраэдр ортасында орналасқан. Катиондар мен молекулалық аниондар арасындағы байланыс ионды (анион мен катион арасындағы кулондық тартылыс күшіне негізделген) байланыс, ал молекулалық анион ішіндегі бөлшектер арасындағы байланыс ковалентті болады. Тетраэдрлік аниондардың орналасуы кристалдарда әр түрлі және әр түрлі бағыттарда қасиеттері айтарлықтай ерекшеленетін әр түрлі анизатропты кристалдарды құрудың, мүмкіншіліктері бар. Біршама үлкен молекулалардан құралған таза молекулалық кристалдар да бар. Осындай кристалдарда әрбір молекула жуық түрде газ фазасындағы бір молекулаларға тән қасиеттерін сақтайды, әйткенмен әлсіз байланыстармен байланысқан реттелген кристалдағы көптеген молекулалар үшін арнайы ұжымдық қасиеттер байқалады (антрацен, нафталин – бензолды сақиналардан тұрады).

Конденсирленген күйді зерттеу ұзақ уақыт бойы бастапқыда қарапайым, кейінірек күрделі идеал кристалдарды зерттеуге бағытталған болатын. Заманауи техника келесі күрделі деңгейге өтуді қажет етті. Кристалдардың өсірілуі (идеал ғана емес нақты кристалдарды да) – бұл қымбат әрі күрделі процесс. Осы күнге дейін, негізінде өлшемі сантиметрмен, ал кейде ондаған сантиметрмен шектелген біршама кіші кристалдар сәтті түрде өсіріліп жатыр. Техникада көбінесе метрмен өлшенетін бұйымдар қажет болып жатады. Сондықтан жүйенің барлық көлемі бойынша аздаған ретсіздікке ие, қатты денелі жүйелерді зерттеуге деген қызығушылық күрт артты. Осында жүйелерге шыныларды жатқызуға болады.

Шыны жоғары температурада балқытылған заттың суытылған пішінге ағылуы кезінде алынады. Мысалы кварц кристалын SiO₂ алайық, ол жоғары температурада балқытылып, кейін бірден тез суытылады. Осы кезде SiO₂ кристалдарына тән бөлшектердің ретпен орналасуы толықтай дерлік қалпына келмейді. Шынылардың микроқұрылымының әбден зерттелуі: кристалдың l>>d қашықтықта орналасқан екі нүктесіндегі тәртіп пен құрылымы бірдей болған жағдайда шыны кристалға тән алыс реттілікті жоғалтатындығын көрсетті. Шыны тәріздес SiO₂ үшін бір бірінен аз қашықтықта орналасқан нүктелер үшін бөлшектердің орналасуы сақталады. Шыны тәріздес күй жақын реттіліктің сақталуымен жуық және алыс реттіліктің болмауымен сипатталады делінеді.Сәйкесінше, шынының кейбір қасиеттері (кристалмен салыстырғанда) әлсіз өзгереді, ал кейбір алыс реттілікті қажет ететін қасиеттері тұтастай өзгереді.

Ескі әдебиеттерде шыныларды жақын реттілікке ие жүйе ретінде талқылаған. Алайда кейінгі зерттеу жұмыстары көрсеткендей шыныда жақын реттіліктің өзі жуық түрде сақталады. Барлық Т кезінде, тіптен Т=0К болғанның өзінде де кристалды құратын бөлшектер қозғалыссыз жағдайда болмайды, олар аз (d – мен салыстырғанда) тербелістер жасайды. Сондықтан кристалдарда қатаң түрде ретті және периодты түрде оларға қатысты атомдар өз тербелістерін жасайтын кристалды тордың түйіндері – тепе теңдік нүктелері ғана орналасады. Ал шыныда, маңында атомдар тербелетін түйіндердің орналасуы кристалдардың жақын орналасқан аймағының аз ерекшелінеді. Барлық шыныда тепе теңдік күйінің шашырауы орын алады, ол жақын қашықтықтарда d – мен салыстырғанда аз және алыс қашықтықта едәуір көп болады. Дегенмен, шынылардағы жақын реттіліктен ауытқуларды нүктелік немесе сызықтық ақау деп талқылауға болмайды, ол шынының іргелі қасиеті.

Конденсирленген күй физикасы кристалдық қатты денелерді электрлік қасиетіне байланысты: диэлектриктер, жартылай өткізгіштер және өткізгіштер деп бөліп қарастырады. Осындай түрлердегі қатты денелердің айырмашылығы 70 жылдан астам бұрын, кванттық механиканың негізінде, қатты денелердің зоналық теориясын жасай отырып талқыланған.

Асқын өткізгіш материалдар туралы естіген шығарсыздар. Төмен температуралы асқын өткізгіштер үшін қандай да бір Т_с сын температурадан төмен Т температурада материалдың электрлік кедергісі секірмелі түрде нөлге дейін төмендейді. Т<Т_с болған жағдайда өткізгіштік электрондары өздерін жеке квазибөлшек сияқты көрсетпейді, олар өздерін кристалдық тордың тербелісімен және ақауларымен әсерлесуін тоқтататын тәртіпті ұжым ретінде көрсетеді. Ұзақ уақыт бойы Т_с ≤ 15К болып келген және қолдану облысы (негізінен, суытылатын магниттер орамы үшін) кіші болған. 1987 жылы бұрын диэлектрлік материалдар ретінде қарастырылған, кейбір метал оксидтерінде температурасы Т_с–дан 80К-ге дейін жоғары температуралы асқын өткізгіш алуға мүмкіншілік болды, 20 жыл ішінде тек 160К-ге дейін жылжуға мүмкіншілік болды. Дәстүрлі асқын өткізгіштермен салыстырғанда жоғары температуралы асқын өткізгіштерде кемтікті (электронды емес) асқын өткізгішті ұжым бар.

1.Бөлім. Идеал кристалдардың геометриясы

1. Монокристалдар. Поликристалдар

Қатты денелер (кристалдар) молекулааралық әсерлесу күштерiнің болуымен сипатталады және көлемiн ғана емес, сонымен қатар пішінін сақтайды.

Кристалдар геометриялық пішіні дұрыс, немiс физигі М. Лауэнің рентгенографиялық зерттеу жұмыстары көрсеткендей, ол кристалды құрайтын бөлшектердiң (атомдар, молекулалар, иондар) ретпен орналасуының нәтижесі болып табылады. Үш өлшемді кеңістікте үнемі (периодты түрде) қайталанумен сипатталатын бөлшектердің орналасуы кеңістіктік тор деп аталады. Бөлшектер орналасқан нүктелер кристалдық тордың түйiндерi деп аталады.

Кристалды денелерді екі топқа бөліп қарастыруға болады: монокристалдар және поликристалдар. Монокристалдар – бөлшектері біртұтас кристалдық тор құратын қатты денелер. Монокристалдардың кристалдық құрылымын сыртқы пішініне қарап айтуға болады. Бір типтегі монокристалдардың сыртқы пішіні әр түрлі болғанына қарамастан онда тиiстi қырлардың арасындағы бұрыштар тұрақты болады.

Бұл 1669 жылы Николай Стенон ашқан бұрыштың тұрақтылық заңы және кристаллографияның осы бiрiншi сандық заңы былай тұжырымдалады: бір типтегі заттың барлық кристалдарында бiрдей жағдайда (температура және қысым бiрдей болғанда) сәйкес кристалл қырларының арасындағы бұрыштар тұрақты болады.

Бұрыштардың тұрақтылық заңы кристалдық көпқырлылардың сан қилы пішіндерін қырлар арасындағы бұрыштар жиынтығына келтіруге және оларды проекция көмегімен бейнелеуге мүмкіндік береді. Рентгендік сәулесі дифракциясын және рентгеноқұрылымды талдау ашылғанға дейін кристалдарды бір бірінен тек қырлары арасындағы бұрыштар арқылы ғана сипаттап және бір-бірінен ажырата білген.

Монокристалдарға көптеген табиғи минералдар: мұзды, ас тұзын, исланд шпатын жатқызуға болады. Қазіргі таңда көптеген монокристалдар жасанды түрде өсіріледі. Ірі монокристалдарды өсіру шарты жиі ұстала бермейді, сондықтан қатты денелердің көпшілігінің кристалдық торлары ұсақ кристалды құрылым түрінде болып келеді, яғни көптеген ретсіз орналасқан ұсақ кристалдық түйірлерден тұрады. Мұндай қатты денелер поликристалдар (көптеген тау жыныстары, техникалық металлдар мен ерітінділер) деп аталады.

Монокристалдарды сипаттайтын ерекшелік олардың анизатроптығы, яғни физикалық қасиеттерінің (серпімділік, механикалық, жылулық, электрлік, магниттік, оптикалық) бағытқа тәуелділігі. Монокристалдардың анизотропиясын мына түрде түсіндіруге болады: кристалдық торда ұзындықтары бойынша бірдей, ал бағыты бойынша түрлі болатын кесіндіге келетін бөлшектердің саны әртүрлі, яғни кристалдық тордағы бөлшектердің орналасу тығыздығы түрлі бағытта бірдей болмайды, сәйкесінше осы бағыт бойынша кристалл қасиеттері де түрленеді. Поликристалдарда анизотропия тек жеке ұсақ кристалшалар үшін байқалады, бірақ олардың әр түрлі орналасуына байланысты барлық бағыт бойынша поликристалдың қасиеті орташа алғанда бірдей.

1.2. Кристалдың трансляциялық симметриясы. Негізгі векторлар

Қатты дене физикасының тарихындағы маңызды кезең Макс фон Лауэ рентген сәулесінің дифракциясы арқылы кристалл атомдардың периодты қатарынан тұратындығын дәлелдеген 1912 жыл болып саналады.

Атомдардың ретпен орналасуы қатты дененің термодинамикалық тепе-теңдік күйіне сәйкес келеді, яғни кристалл – бұл жеткілікті төмен температурада атомдар жүйесінің тепе-теңдік күйі. Барлық қатты денелер кристалдық бола бермейді: мысалы, балқыған немесе еріген затты тез суытқан кезде ''мұздатылған сұйықтықты'' – атомдары ретсіз орналасқан, аморфты қатты денені алуға болады. Мұндай қатты денелердің мысалы ретінде қарапайым шыныны алуға болады. Кристалда атомдардың ретпен орналасуы деп оның кеңістіктіктегі периодтылығы мегзеледі. Басқаша айтқанда, әрбір кристалл үшін бір жазықта жатпайтын және кристаллды біртұтас түрінде осы векторлардың кез келгеніне орын ауыстырғанда өзіне-өзі қайта беттесетін үш вектор таңдап алуға болады.

Кристалдың векторына орын ауыстыру операциясы трансляция деп аталады, мұндағы n₁, n₂, n₃ — бүтін сандар. Кристалдар трансляциялық симметрияға ие дейді, өйткені векторына трансляциялану барысында ол өзіне өзі беттеседі. векторларын түрлі әдістермен таңдап алуға болатындығы анық (1-суретті қара). Осы векторлар арқылы жасалған параллелепипед элементар ұяшық деп аталады. Минималь көлемді ұяшық примитивті ұяшық, ал ол құрылған векторлары трансляцияның примитивті немесе негізгі векторлары деп аталады. Кейін де трансляцияның басты векторлары дәл осылай белгіленеді. векторларын біз тура тордың векторлары деп атаймыз. Осылайша, примитивті ұяшық элементар ұяшықтың жеке жағдайы болып табылады. Басты векторларды да түрлі әдістермен таңдауға болады.

1-суретте екі негізгі 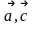және негізгі векторлардың екі мүмкін жұптары келтірілген, ал екі мүмкін болатын негізгі векторлардың жұбы, ал ,— трансляцияның негізгі емес векторлары.

Примитивті ұяшықтың көмегімен трансляцияның кейінгі операциялары арқылы, кристалдық құрылымның барлық кеңістігін толтыруға болады. Примитивті ұяшық – бұл кеңістікте периодты түрде қайталанатын, параллелепипед пішінді, әр нүктесінде атомдар жиынтығымен байланысты кристалдық тордың бір бөлігі. Мұндай атомдар жиынтығын базис деп атайды, базис кеңістікте қайталанады және кристалдық құрылымды түзеді.

Трансляцияның негізгі векторымен құрылған кристалдың примитивті ұяшығы бар делік. Кеңістіктегі бір нүктені алып және векторына осы нүктенің трансляциясы арқылы нүктелерден тұратын кеңістіктік торды аламыз, мұндағы n₁, n₂, n₃ барлық бүтін сандарды алады. Осы тордағы барлық нүктелер (түйіндер) эквивалентті, яғни айналасы бірдей болатындығын көре аламыз (басқаша айтқанда, әрбір түйіннен қарағанда тордың бір бейнесін ғана көре аламыз). Осындай торлар Бравэ торлары деп аталады. Бравэ торлары кристалдың трансляциялық симметриясын толықтай көрсетеді. Трансляцияның негізгі векторлары келесі шарттарды қанағаттандыруы керек: Бравэ торының қандай да бір түйінінен басталатын және оның бойында құрылған тура тордың векторлары Бравэ торының барлық басқа түйіндерінде аяқталуы қажет, яғни тура тордың векторларының ішінде берілген Бравэ торының кез-келген екі түйінін қосатын векторлар табылады. Егер кристалдық тордың базисі бір ғана атомнан тұратын болса және бір примитивті ұяшықта бір ғана атом орналасса, онда кристалдық тор қарапайым деп аталады. Бұл жағдайда кристалдың барлық атомдары бір Бравэ торының түйіндеріне орналасады. Егер примитивті ұяшықты, оған тек бір атом сәйкес келетіндей етіп таңдап алу мүмкін болмаса, яғни базис бірнеше атомдардан тұрса, онда тор күрделі болады. Бұл жағдайда базистің әр атомына, өзінің бір типтегі атомдардан тұратын торшасы сәйкес келеді және ол кристалдың Бравэ торына ұқсас. Екіөлшемді күрделі тордың мысалы 1.1-суретте бейнеленген. Қара және ақ атомдар химиялық тұрғыдан ұқсас болуы мүмкін, бірақ ереже бойынша олардың кристалдық торларда орналасуы әртүрлі. Егер кристалдағы атомдар химиялық тұрғыдан ұқсас болса және олардың әрбірінің қай жағынан қарасаң да кристалдық тордың бір бейнесі көрінсе, онда сол атомдар бір типті болады. Осылайша, егер тек бір типті атомдарға ғана қарасақ Бравэ торын көре аламыз. Кристалды екі әдіс арқылы көзге елестетіп, түсінуге болады: базисті алып, трансляцияның примитивті векторлары көмегімен оны көп рет трансляциялау керек немесе бірнеше бірдей Бравэ торларын алып, оларды бірінің үстіне бірін орналастыру керек. Екіөлшемді кристалл, 1.1-суретте көрсетілгендей, бірінің үстіне бірін орналастырған екі Бравэ торынан тұрады

1.1 сурет. Екі өлшемді Бравэ торы

1.2 сурет. Қарапайым кубты тор

1.2–суретте қарапайым кубты тор көрсетілген. Қырғацентрленген кубты тордың әрбір ұяшығында бір ғана атом орналасқан (1.3–сурет).

1.3 сурет. Кубты гранецентрленген

Егер кубтың ортасында атом болса, онда ол көлемді-центрленген кубты тор делінеді (1.4–сурет.).

1.4 сурет. Көлемді-центрленген кубты тор

Сонымен, Бравэ торы кристалдың кұрылысын емес, оның трансляциялық құрылымын (симметриясын) көрсетеді. Трансляциядан басқа, кристалдардың нүктелік симметриясы: бұрылыс пен шағылысуға қатысты симметриясы болады. Нүктелік симметрияны анықтау үшін Бравэ торының типімен бірге, байланыс құрылыстарын да ескеру қажет (примитивті ұяшықтың базисі). Кейде қарапайым ұяшық дегенде базис пен примитивті ұяшықты көзге елестетуге болатындығын айтып кетейік. Бірнеше примитивті ұяшықтары бар және кристалдың нүктелік симметриясын көрсететін Бравэ торының бір бөлігін шартты немесе кристаллографиялық қарапайым ұяшық дейді. 1.2-1.4-суреттерде дәл осындай ұяшықтар бейнеленген.