4.3.3. Діапазон вихідних значень

Діапазон вихідних значень (FSO) — алгебраїчна різниця між електричними вихідними сигналами, обмірюваними при максимальному й мінімальному зовнішньому впливі. У цю величину повинні входити всі можливі відхилення від ідеальної передатної функції. На рис.2.2А величина SFS відображає діапазон вихідних значень.

4.3.4. Точність

Коли говорять про точність датчика, найчастіше мають на увазі погрішність вимірів. Під погрішністю вимірів, як правило, розуміють величину максимальної розбіжності між показаннями реального й ідеального датчиків. Уважається, що обмірюване значення відповідає реальному з певним ступенем вірогідності.

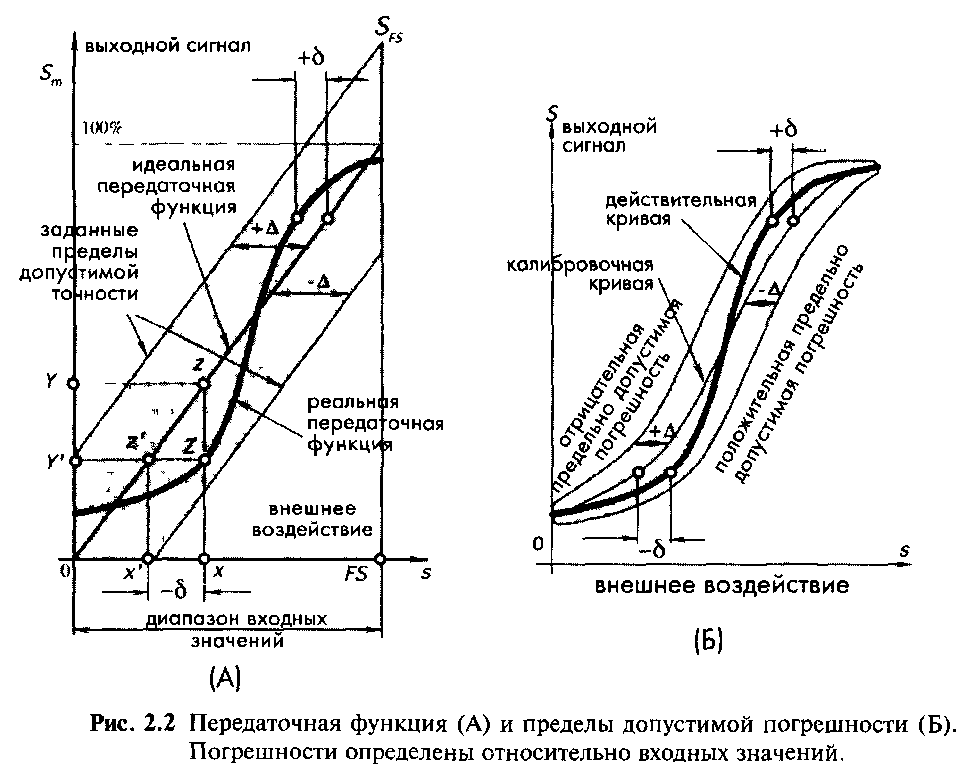
Рис. 4.4 Передатна функція (А) та межа припустимої похибки (Б). Похибки визначаються відносно вхідних значень

Погрішність датчика можна також представити у вигляді різниці між значенням, обчисленим по вихідному сигналу датчика, і реальним значенням поданого вхідного сигналу. На рис.4.4А показана ідеальна або теоретична передатна функція. Товстою лінією на малюнку виділено одна з реальних передатних функцій, які не обов'язково є лінійними й монотонними. Навіть коли датчики виготовляються в ідентичних умовах, через різницю в матеріалах, у майстерності працівників, помилок розроблювачів, виробничих допусків і т.п., їхні передатні функції завжди будуть різнитися друг від друга. Однак усі вони не повинні виходити за межі певної зони, що лежить у границях гранично припустимих погрішностей, які перебувають від лінії ідеальної передатної функції на відстані ±. В ідеальному випадку вихідний сигнал повинен бути рівний Y, що відповідає крапці z на передатній функції. Замість цього по реальній функції при значенні х ми потрапимо в крапку Z, і, отже, одержимо вихідний сигнал, рівний Y' відповідний до крапки z' на ідеальній передатній функції, якої, у свою чергу, повинен відповідати вхідний сигнал х' Оскільки х' < х, погрішність вимірів у цьому випадку буде рівна -.

На точність датчиків впливають такі характеристики як: гістерезис, мертва зона, параметри калібрування, повторюваність датчиків від партії до партії й відтворюваність погрішностей, які будуть розглянуті в наступних розділах. При більш коректному калібруванні (калібрування на більшій кількості точок, рис.4.4Б), калібрована крива проходить ближче до реальних передатних функцій, що означає підвищення точності вимірів. На практиці межі припустимих погрішностей установлюються не навколо ідеальної передатної функції, а щодо каліброваної кривої.

Погрішність датчиків може бути представлена в наступних видах:

1. Безпосередньо в одиницях вимірюваної величини (А),

2. У відсотках від значення максимального вхідного сигналу,

3. В одиницях вихідного сигналу.

У сучасних датчиках точність часто характеризується величиною статистичної помилки вимірів, що враховує вплив як систематичних, так і випадкових погрішностей, що й не залежать від помилок, допущених при визначенні передатних функцій.

4.3.5. Калібрування

Якщо виробничі допуски на датчик і допуски на інтерфейс перевищують необхідну точність системи, завжди необхідно проводити калібрування. Наприклад, потрібно виміряти температуру з точністю ±0.5°З датчиком, за довідковим даними, що володіють погрішністю ± 1 °С. Це можна зробити тільки після проведення калібрування. У процесі проведення повного калібрування визначаються коефіцієнти, що описують передатну функцію всієї системи в цілому, включаючи датчик, интерфейсний пристрій і АЦП.

Для нелінійних функцій калібрування потрібно проводити більш ніж у двох крапках. Кількість необхідних калібрувань диктується видом математичного вираження. Якщо передатна функція моделюється поліномінальною залежністю, число каліброваних крапок вибирається залежно від необхідної точності. Оскільки, як правило, процес калібрування займає досить багато часу, для зниження вартості виготовлення датчиків на виробництві кількість каліброваних крапок задається мінімальним.

Застосування кусково-лінійної апроксимації є іншим підходом до калібрування нелінійних датчиків. Як згадувалося вище, будь-яку криву в межах досить невеликого інтервалу можна замінити лінійною функцією.

Для проведення калібрування датчиків важливо мати точні фізичні еталони, що дозволяють моделювати відповідні зовнішні впливи. Наприклад, при калібруванні контактного датчика температури його необхідно поміщати або в резервуар з водою, або в «сухий колодязь», у яких є можливість точно регулювати температуру. При калібруванні інфрачервоних датчиків потрібне наявність чорного тіла, а для калібрування гігрометрів — набір насичених розчинів солей, використовуваних для підтримки постійної відносної вологості в закритому контейнері і т.д. Звідси ясно видне, що точність наступних вимірів прямо пов'язана з точністю проведення калібрування. Помилка каліброваних еталонів повинна включатися в повну помилку вимірів.