1. Цель страхования. Простейшая математическая модель страхования (с позиции страхователя), критерии справедливости и выгодности страхования для страхователя.

Цель страхования заключается в снижении ущерба при наступлении несчастных случаев, катастрофических событий и др, несущее последствия, потерю имущества или здоровья людей. Страховым случаем счит.такое событие, кот.обладает вероятностым и случайным характером. Событие влечет появление стр.случаев. Пусть

P – Вероятность наступления страхового случая

C – Стоимость имущества застрахованного

S – Величина, на которую застраховано имущество

k – уровень страхового покрытия

S = kC

d – премия (взнос) страхователя страховщику попериодно

	q	p	EX	DX	у
Без страхования	0	C	pc	pqcІ	c√pq
Со страхованием	d	d+(1-k)C	d+p(1-k)C	(1-k)І сІ pq	C(1-k) √pq

d=pc

если покрытие полное, то дисперсия и отклонение равны нулю.

(.)1 – не страх., k=0, большой риск потерь

(.) 2 – страхуем, но K< 1, риск остается, но снижен

(.) 3 – идеальный случай, K=1, стр.полностью и риск нулевой

(.) 4 – реальный случай, 0 < k < 1, присутствует доля риска

(.)5 –может быть

Чтобы не уходить с линии, нбх d= pkC

Реально d>pkc

Когда есть смысл страховать? Выгодность страхователя связана с тем, насколько доходен его бизнес (т.к. он отдает часть дохода/прибыли) и какова его оценка вероятности ущерба (риска) – тариф.

2. Математическая модель системы "страхователи-страховщик", условие существования компромиссного решения.

Y – капитал, который имеет страховщик

Yi – капитал страхователя

C – начальный капитал страхователя

U(.), Ui(.) – функции полезности страховщика \ страхователя

X- возможный ущерб страхователя (случайная величина)

Z – возможный ущерб страховщика (случайная величина)

d – взнос, который платит страхователь страховщику

n – количество страхователей

Функция полезности (ввел Госсен)

Полезность выигрыша 1 меньше, чем полезность выигрыша 2, и меньше с каждым шагом.

Субъект (или ЛПР) не склонен риску – прибавка полезности при выигрыше меньше, чем потеря полезности при проигрыше, и рисковать невыгодно.

Если функция полезности линейная, то ЛПР к риску нейтрален.

Для заключения контракта необходимо разное отношение к риску – ЛПР д.б осторожен.

D=n*d = ∑di – суммарные взносы

Функция полезности страховщика:

U( Y+D - ∑ Zi) > U(Y) – условие его заинтересованности

Ф1(d) =EU(Y+D-∑Zi) – U(Y) –приращение полезности для страховщика

C точки зрения страхователя:

Страхователю выгодно страховать, если его полезность после страхования >, чем полезность без страхования.

Ui(Yi – d) –если страхователь застрахуется.

Ф2=Ui(yi-d) –E Ui(yi-Zi)

Ui(yi-d) > E Ui(yi-Zi)

Если Ф2 >0, то стоит страховать.

Для страховщика, чем больше d, тем ему лучше, для страхователя – наоборот.

d′d′′ - и страховщик и страхователь в «плюсах».

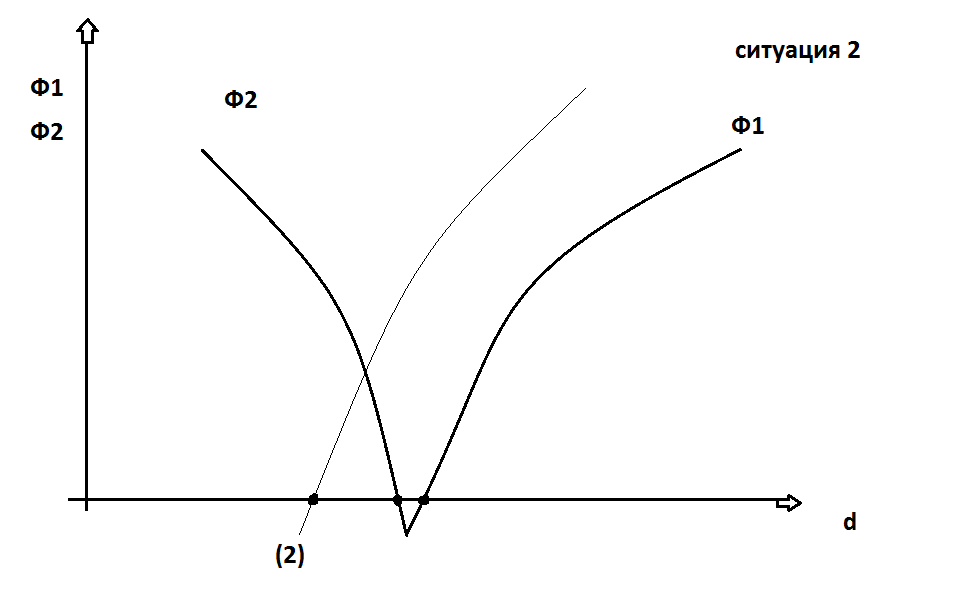
Нет выгоды в такой ситуации.

Функции Ф1 и Ф2 связаны не только с d, но и с n. При большем n Ф1 «уходит» влево и договорное множество может появиться. Чем >n, тем страховщик может снизить величину d, те (2)-см график.