Часть 1. Составление исходной матрицы и проведение корреляционного анализа

Задание 1. Составить матрицу исходных данных, факторов, влияющих на исследуемые выходные параметры на основе наблюдений, опроса специалистов или на основе факторного анализа ( 5Х5 – пять факторов, пять уровней, 4Х4 – четыре фактора, 4 уровня). Предметная область выбирается студентом самостоятельно.

Задание 2. Составить программу расчета на основе предложенных расчетных формул и алгоритма ( на любом языке программирования : при представлении результатов вычислений в виде экранных форм, можно использовать элементы MSFlexGrid в VBA; Delph и др. языки программирования по выбору студента ).

Наличие связи между факторами устанавливается с помощью коэффициентов корреляции.

На базе статистических (исходных данных таблицы задания 1 ) X_kj; k = 1,n; j = 1,m для m-параметров в n наблюдениях формируется матрица коэффициентов корреляции (рис.3) между параметрами состояния системы:

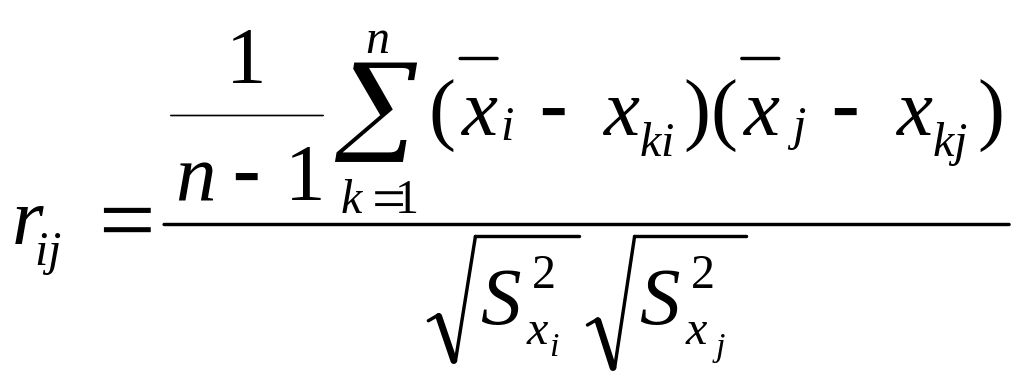; i,j = ; , ( 1 )

где – среднее значение i-го и j-го факторов;

– дисперсии i-го и j-го факторов.

Задание 3. На основе результатов вычислений провести корреляционный анализ, сделать соответствующие выводы и оформить отчет по выполненной работе.

Часть 2. Проведение регрессионного анализа и приведение системы в безразмерный вид.

Задание 1 . Разработать матрицу коэффициентов регрессии (использовать данные предыдущих заданий и выбранной студентами предметной области самостоятельно ).

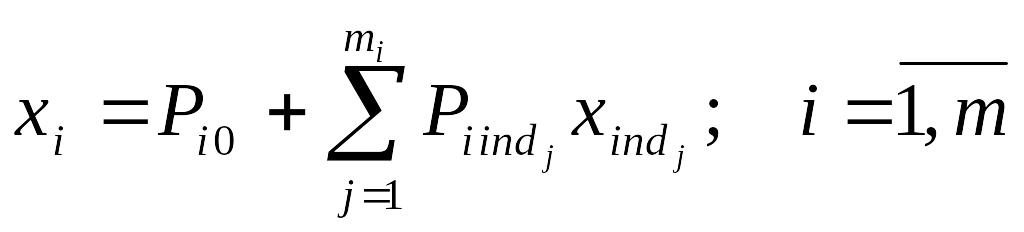Матрицы коэффициентов регрессии разрабатывается следующим образом: для каждой строки матрицы r_ij; i,j =1,m составляется индексный массив Ind_j параметров, тесно связанных с i-м фактором, и находятся коэффициенты линейной множественной регрессии, отражающие характер линейных связей между коррелируемыми факторами (рис.4).

где P_ij – коэффициент линейной множественной регрессии между i-м и j-м факторами X_i, X_j.;.

Найденные коэффициенты записываются в регрессионную матрицу P_ij; i,j = 1,m.

Задание 2. Привести систему в безразмерный вид ( использовать исходные данные предыдущих заданий выбранной предметной области самостоятельно ).

Для получения сопоставимых характеристик влияния и связей между параметрами матрица коэффициентов регрессии пересчитывается в матрицу

б езразмерных сопоставимых характеристик связей:

( 2 )

где: σ_i, σ_j – среднеквадратичные отклонения i-го и j-го факторов от математического ожидания;

Получаемая в результате пересчета матрица сопоставимых оценок взаимосвязей может быть скорректирована с учетом логики процессов и операций в системе (в зависимости от исследуемой предметной области).